Вопрос 14 Арифметические операции над функциями, имеющими предельное значение

Теорема. Пусть, заданные на одном и том же множестве функции и имеют в точке предельные значения и . Тогда функции , , и имеют в точке предельные значения (частное при условии, что ), равные соответственно , , и .

Следствие. Если функция имеет в точке предельное значение, равное , то .

Действительно, пусть . Воспользовавшись предыдущее теоремой, получим

.

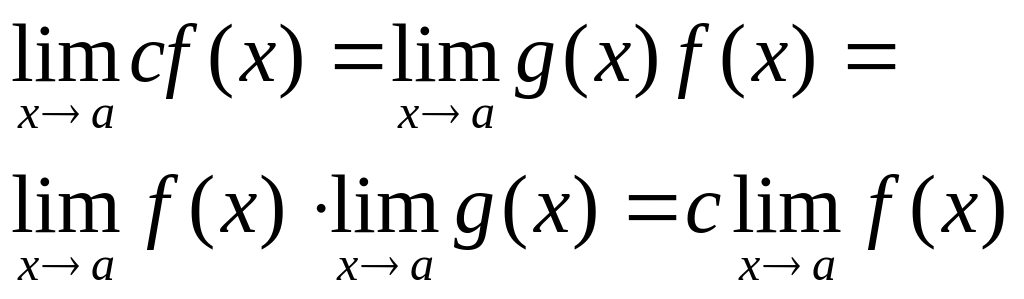Заметим, что данная теорема также справедлива в случае, когда .

Вопрос 15 Предельный переход в неравенствах.

Будем называть проколотой окрестностью точки , множество точек этой окрестности за исключением самой точки .

Теорема 1. Если функция имеет в точке предельное значение, равное , и в некоторой проколотой окрестности точки справедливо неравенство , то .

Теорема 2. Если функции и имеют в точке предельные значения, равные и , и в некоторой проколотой окрестности точки справедливо неравенство , то .

Теорема 3. Если функции и имеют в точке одинаковые предельное значение, равные , и в некоторой проколотой окрестности точки справедливо неравенство , то функция также имеет в точке предельное значение, равное .

Докажем для примера теорему 3. Две других доказываются аналогично. Возьмем произвольную последовательность , сходящуюся к , все элементы которой находятся в указанной в теореме проколотой окрестности точки . Тогда , и . По теореме о трех последовательностях существует предел соответствующей последовательности значений функции , равный . Поскольку , то существует предельное значение функции в точке , равное .

Заметим, что теоремы 1-3 справедливы и при , если указанные в их формулировках неравенства выполняются при условии , где — некоторое положительное число.

Вопрос16 Первый замечательный предел

Теорема. Предельное значение функции в точке существует и равно единице:

. (1)

Равенство (1) называют первым замечательным пределом.

Доказательство. Если , то справедливо неравенство

.

Разделим его на . В результате получим

,

откуда имеем

. (2)

В силу четности функций и неравенство (2) справедливо и для . Поскольку , то из неравенства (2) следует, что функции также имеет в точке предельное значение, равное единице.

Следствие. .

Вопрос 17 Второй замечательный предел

Теорема. Предельное значение функции при существует и равно :

.

Второй замечательный предел также записывают в виде .

Пример. Банк принимает деньги у населения под % годовых. Во сколько раз возрастет сумма вклада за год, если проценты начислять : 1) в конце года; 2)в конце каждого месяца (с пересчетом суммы вклада); 3)«ежемгновенно».

1) Пусть — первоначальная сумма вклада. Тогда через год она увеличится на величину , то есть вырастет в раз.

2) Если проценты начисляются ежемесячно, то по истечению первого месяца сумма вклада увеличится на величину и будет равна , то есть увеличится в раз. Через месяц на сумму опять начислят %, и вклад снова увеличится в раз. Таким образом, через год на счету вкладчика будет сумма в раз большая первоначального вклада.

3) Разделим год на периодов. По истечению каждого периода банк начисляет %, пересчитывая сумму вклада. Тогда через год сумма вклада возрастет в раз. Устремим и найдем предельное значение . Введем обозначение . Очевидно, что при . Тогда

.

Итак, если проценты начислять «ежемгновенно» то сумма вклада возрастет за год в раз.