Вопрос 35 Производные обратных функций

Рассмотрим функцию . Эта функция определена на интервале и служит обратной для функции , определенной на интервале . Функция непрерывна, строго монотонна на интервале и в любой точке этого интервала имеет конечную производную , отличную от нуля. По теореме о производной обратной функции имеем

.

Функция определена на интервале и служит обратной для функции , определенной на интервале . Функция непрерывна, строго монотонна на интервале и любой точке этого интервала имеет конечную производную . Тогда по теореме о производной обратной функции получим

.

Функция , определенная на бесконечной прямой , является обратной для функции , определенной на интервале . Для функции на интервале выполнены все условия теоремы о производной обратной функции. Заметим также, что . Тогда

.

Функция , определенная на бесконечной прямой , является обратной для функции , определенной на интервале . Для функции на интервале выполнены все условия теоремы о производной обратной функции. Заметим также, что . Тогда

.

Вопрос 36 Производной сложной функции

Теорема. Пусть функция дифференцируема в некоторой точке , а функция дифференцируема в точке . Тогда сложная функция дифференцируема в указанной точке и справедлива следующая формула

. (1)

Доказательство смотри в [1] на стр. 175.

Используем данную теорему для вычисления производных гиперболических функций. Найдем вначале производную функции . Введем переменную и, будем рассматривать функцию как сложную функцию . Используя формулу (1), получим

.

Далее имеем

,

,

,

.

Вопрос 37 Логарифмическая производная

Пусть функция положительна и дифференцируема в данной точке . Тогда в этой точке существует . Рассматривая как сложную функцию аргумента , можно вычислить производную этой функции, принимая за промежуточный аргумент. Получим

.

Эта производная называется логарифмической производной функции в данной точке .

Вопрос 39

Гиперболические функции. Гиперболическими называются следующие функции:

1. — гиперболический синус;

2. — гиперболический косинус;

3. — гиперболический тангенс;

4. — гиперболический котангенс.

Поскольку показательная функция непрерывна на всей числовой прямой и принимает только положительные значения, то из определения гиперболических функций следует, что функции также непрерывны на всей числовой прямой, а гиперболический котангенс определен и непрерывен всюду на числовой прямой, за исключением точки .

Отметим некоторые свойства гиперболических функций:

Док-во.

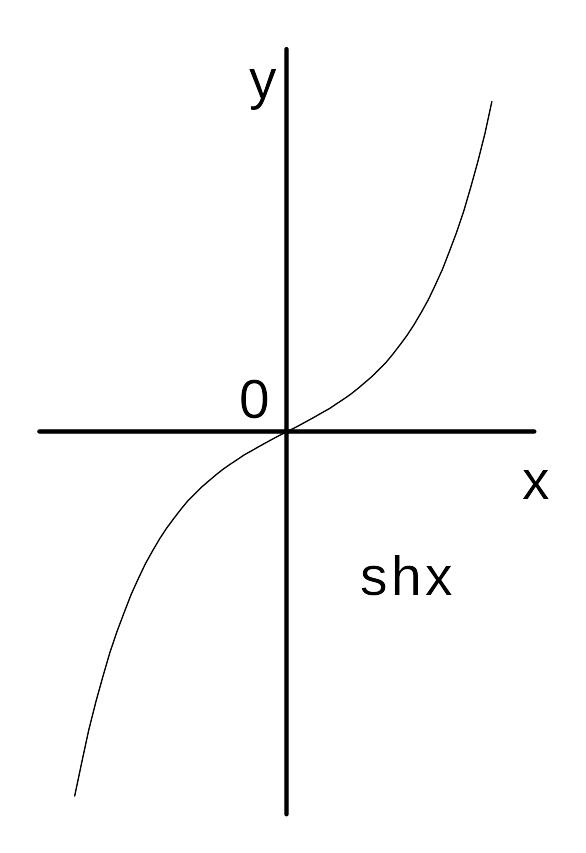
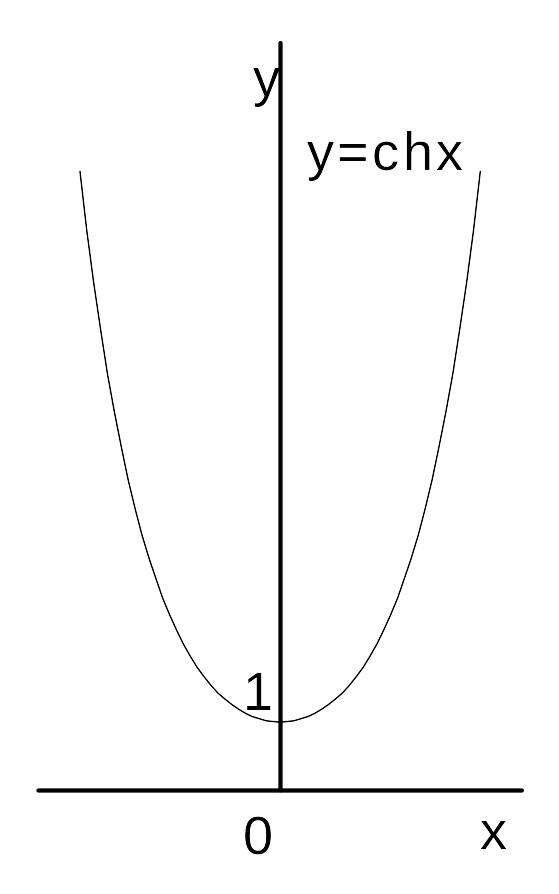
Рис. 6

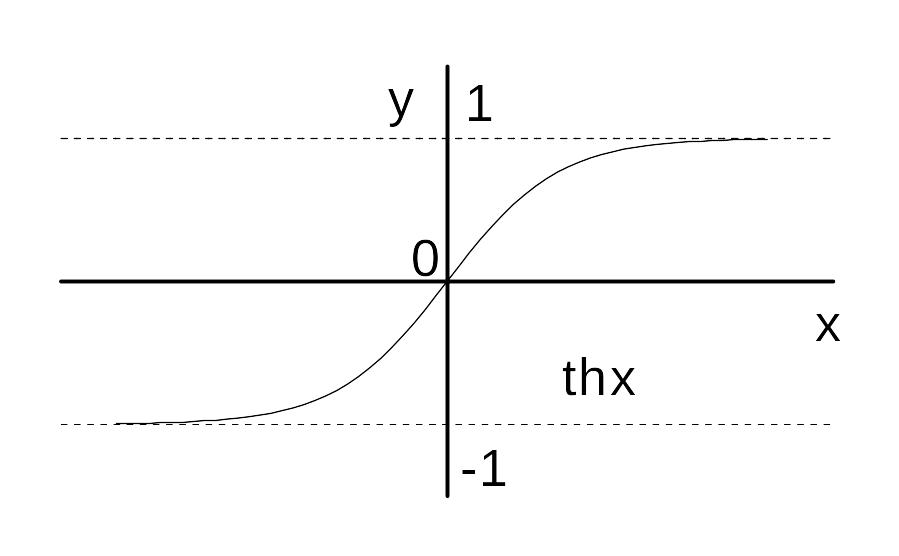
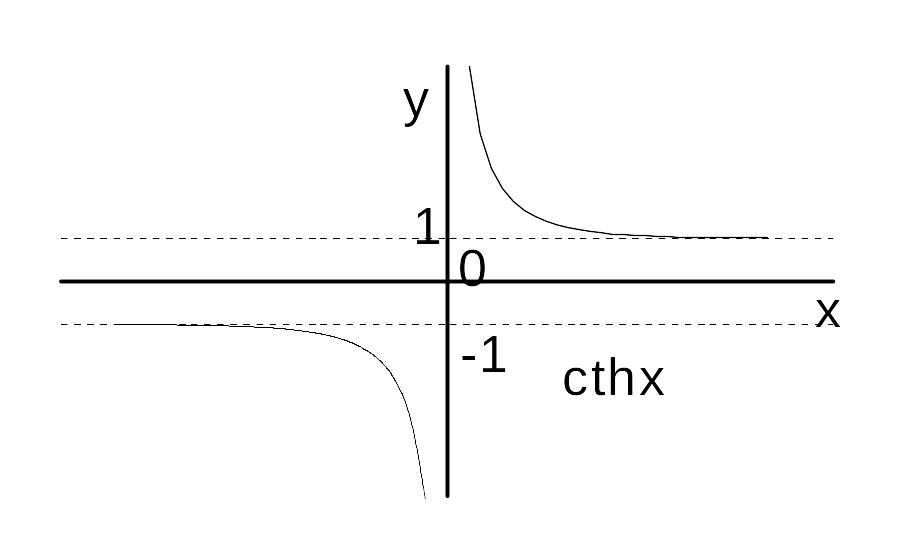
Вопрос 42

Теорема Ферма (необходимое условие локального экстремума дифференцируемой функции). Если функция дифференцируема в точке и имеет в этой точке локальный экстремум, то .

Доказательство. Пусть функция определена в некоторой окрестности точки , и пусть точка является точкой локального максимума. Тогда для всех , принадлежащих данной окрестности, справедливо неравенство . Следовательно, если , то

(1)

а если , то

(2)

Если функция дифференцируема в точке , то в этой точке существует производная , то есть существует конечный предел . Переходя в неравенстве (1) к пределу при получим . Аналогично из неравенства (2) находим . Но если функция имеет производную в точке , то правая и левая производные должны быть равны друг другу. Это возможно только в том случае, если . Следовательно, .

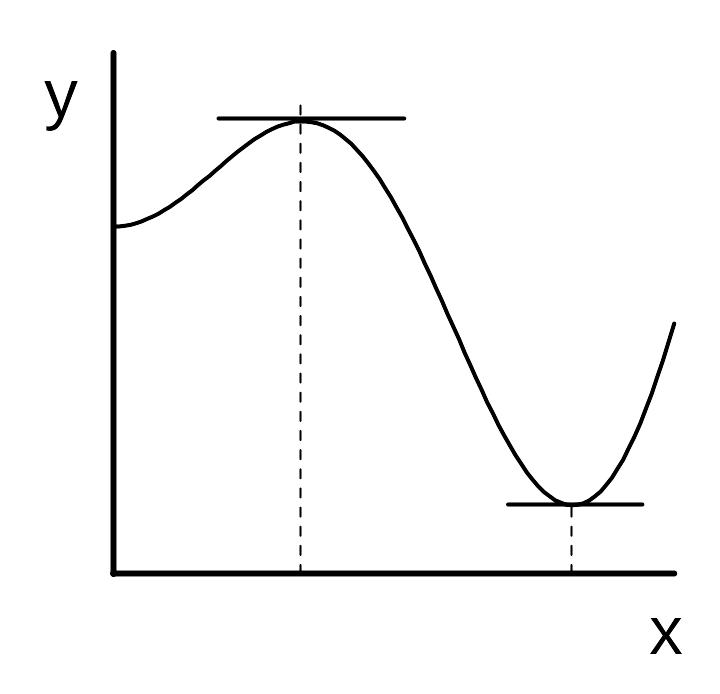
Геометрическая интерпретация теоремы Ферма состоит в том, что, если в точке дифференцируемая функция имеет локальный экстремум, то касательная к графику функции, проведенная в точке , параллельна оси (рис. 1). Действительно, если — угол наклона касательной, то . Следовательно, .

Заметим, что условие не является достаточным условием экстремума функции в точке . Например, производная функции равна нулю в точке , но не имеет в этой точке экстремума Рис. 1

(рис. 2). Заметим также, что недифференцируемые в точке функции могут иметь в этой точке экстремум. Например, функция не дифференцируема в точке , однако имеет в этой точке локальный минимум. Действительно, для любого справедливо неравенство (рис. 3).

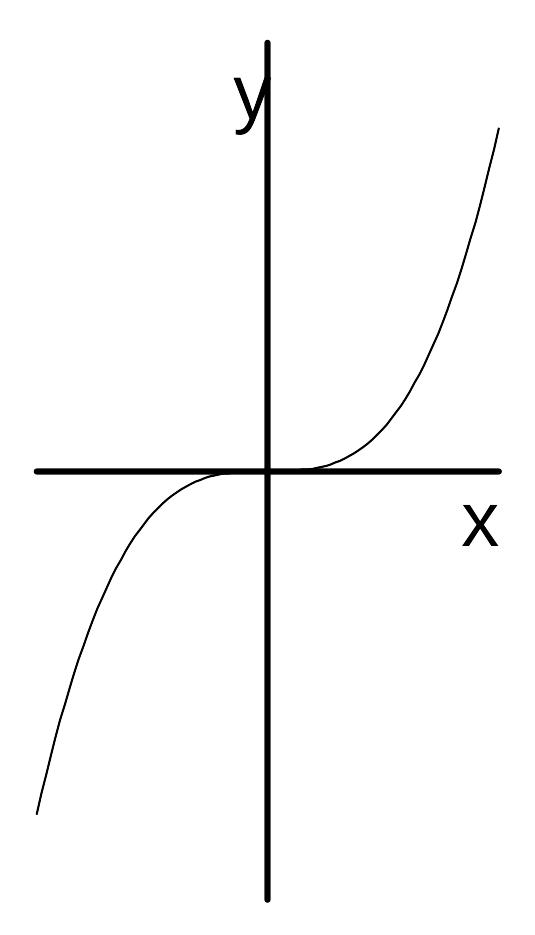
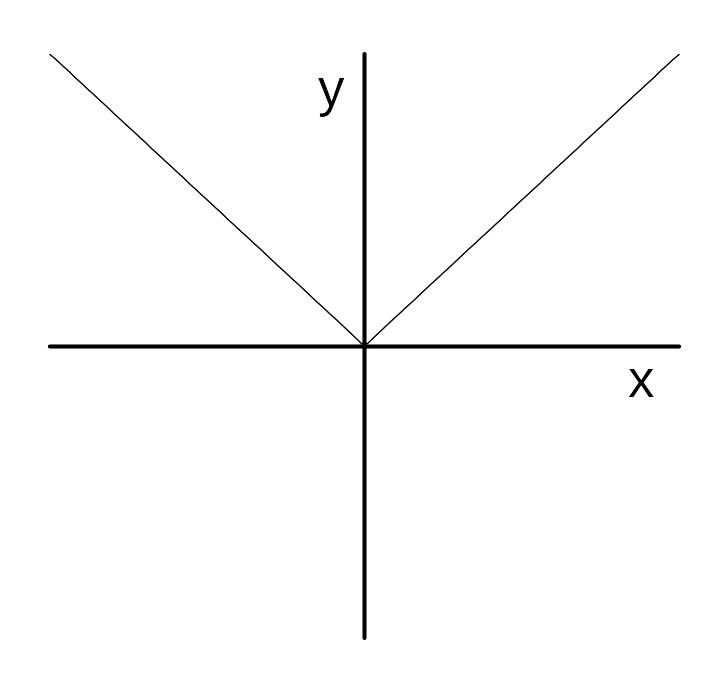
Рис. 2 Рис. 3