Вопрос 31 Понятие производной

Определение 1. Пусть функция определена в некоторой окрестности точки . Зададим аргументу приращение такое, что значение находится в указанной окрестности точки . Приращением функции в точке , соответствующим приращению аргумента называется число

. (1)

Определение 2. Производной функции в точке называется конечный предел (если он существует) при отношения приращения функции в этой точке к соответствующему приращению аргумента.

Производную функции в точке будем обозначать символом или . По определению производной

(2

Если функция определена на некотором интервале , то в любой фиксированной точке этого интервала аналогичным образом определяются приращение и производная в точке :

,

. (2’)

Примеры вычисления произ.

1. , где — некоторая постоянная.

Для данной функции и .

2. .

.

3. .

,

.

4. .

,

.

Из последней формулы следует, что

.

5. .

,

.

В частном случае, при , имеем

.

6. , где — натуральное число.

Воспользовавшись формулой бинома Ньютона получим

,

Односторонние производные

Определение. Если функция определена в некоторой правосторонней (левосторонней) окрестности точки и существует правый (левый) предел

(3)

, (4)

то этот предел называется правой (левой) производной.

Заметим, что, если функция имеет в точке производную, то это означает, что существует конечный предел

.

Следовательно, существуют конечные правый и левый пределы (3) и (4), равные , то есть функция имеет в точке правую и левую производные, равные .

Верно и обратное утверждение: если в точке функция имеет правую и левую производную, и если эти производные совпадают между собой, то у нее в этой точке существует производная, равная правой и левой производной.

Если же в некоторой точке существуют отличные друг от друга правая и левая производная, то функция в этой точке производной не имеет, поскольку не существует предела .

Пример. Рассмотрим функцию

Найдем правую и левую производную данной функции в точке :

,

.

Поскольку в точке получились разные значения правой и левой производной, то это означает, что в данной точке у функции производной не существует.

Геометрический смысл производной

Пусть функция определена на некотором интервале и непрерывна в точке , принадлежащей этому интервалу. Пусть , , . В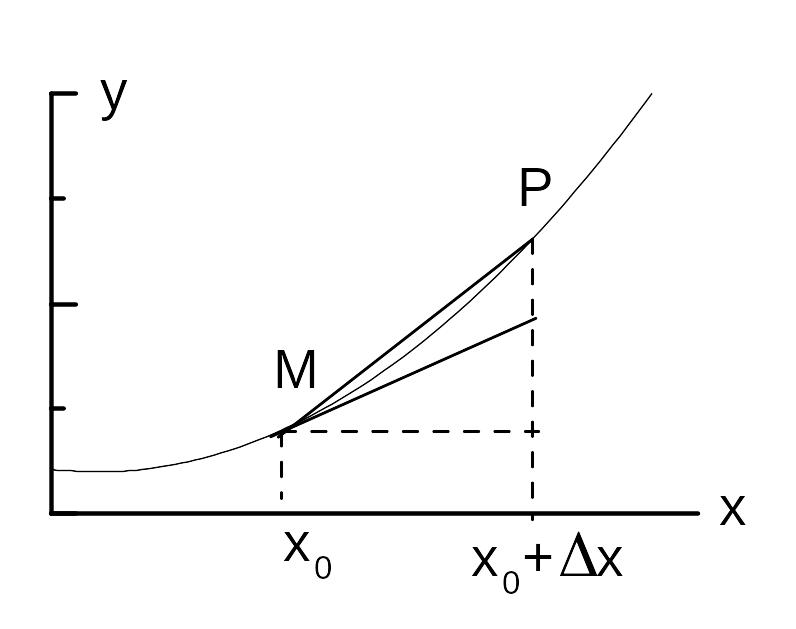 озьмем на графике функции две точки: и . Заметим, что

, следовательно, точка имеет координаты . Проведем секущую .

Касательной к графику функции в точке будем называть предельное положение секущей при стремлении точки к точке , то есть если расстояние .

Покажем, что расстояние стремится к нулю при . Действительно, и, в силу непрерывности функции в точке , . Следовательно, .

Итак, касательная к графику функции в точке — это предельное положение секущей при .

Предположим, что функция имеет производную в точке , и докажем, что график функции имеет в данной точке касательную, а угловой коэффициент указанной касательной равен .

Обозначим угол наклона секущей через . Этот угол, очевидно, зависит от . Найдем угловой коэффициент секущей

.

Угловой коэффициент секущей при стремится к угловому коэффициенту касательной к графику функции в точке , то есть

.

Итак, производная функции в точке равна тангенсу угла наклона касательной к графику функции, проведенной в точке . Уравнение касательной имеет вид или .

Заметим, что если , то . В этом случае касательная перпендикулярна оси и имеет уравнение .