Вопрос 9 Монотонные последовательности

Определение. Последовательность называется неубывающей (невозрастающей), если каждый последующий член последовательности не меньше (не больше) предыдущего, то есть для всех номеров справедливо неравенство

( ).

Неубывающие и невозрастающие последовательности называются монотонными.

Если каждый последующий член последовательности строго больше (меньше) предыдущего, то последовательность называется возрастающей (убывающей). В этом случае для всех номеров справедливо неравенство ( ). Возрастающие и убывающие последовательности называются строго монотонными.

Пример. Последовательность убывающая. Действительно, , следовательно, .

Признак сходимости монотонной последовательности

Теорема Вейерштрасса. Если неубывающая (невозрастающая) последовательность ограничена сверху (снизу), то она сходится.

Заметим, что невозрастающие и убывающие последовательности заведомо ограничены сверху своим первым элементом, поскольку для всех номеров справедливо неравенство . Если они к тому же ограничены снизу, то они ограничены с двух сторон.

Неубывающие и возрастающие последовательности всегда ограничены снизу своим первым элементом, так как для всех номеров справедливо неравенство . Для того, чтобы они были ограничены, достаточно потребовать, чтобы они были ограничены сверху.

Учитывая эти замечания, теорему Вейерштрасса можно также сформулировать следующим образом: если монотонная последовательность ограничена, то она сходится.

Вопрос 10 Предел последовательности

Для исследования сходимости последовательности воспользуемся теоремой Вейерштрасса. Докажем, что эта последовательность возрастающая и ограниченная. Применяя формулу бинома Ньютона

где — биномиальные коэффициенты, которые вычисляются по формуле , получим

.

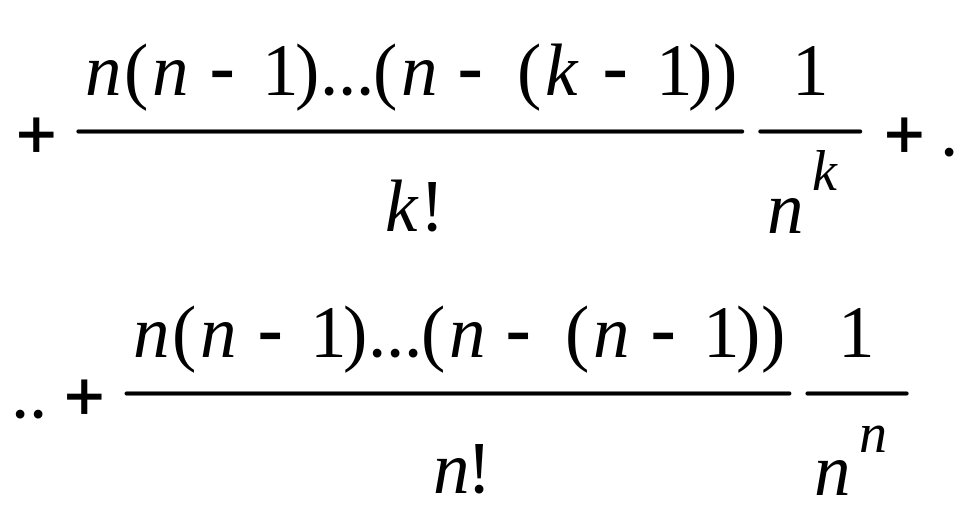Заметим, что . Тогда выражение (1) примет вид

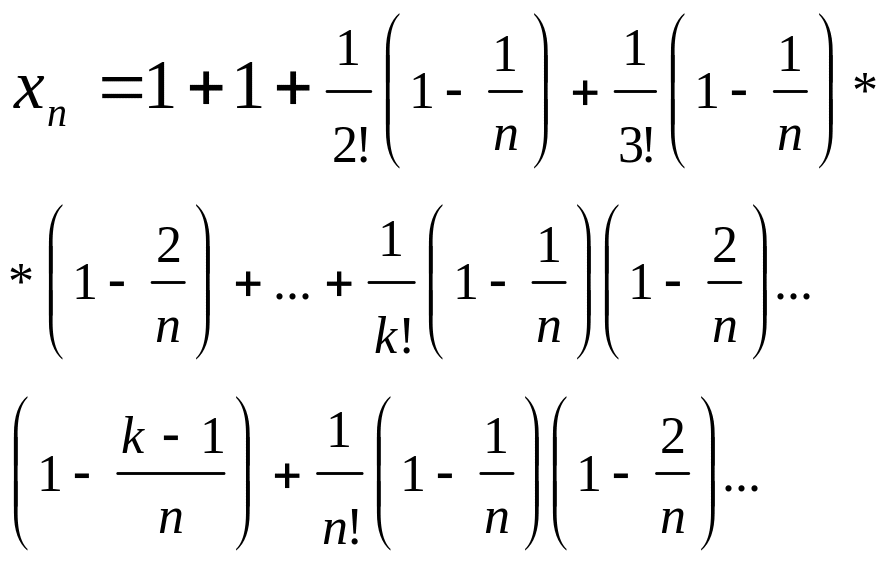
. (2)

Аналогично получим выражение для элемента

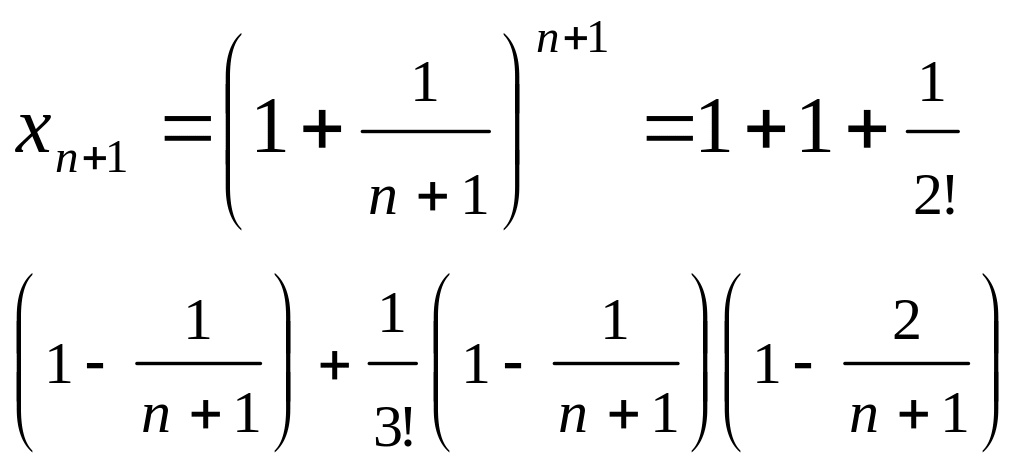
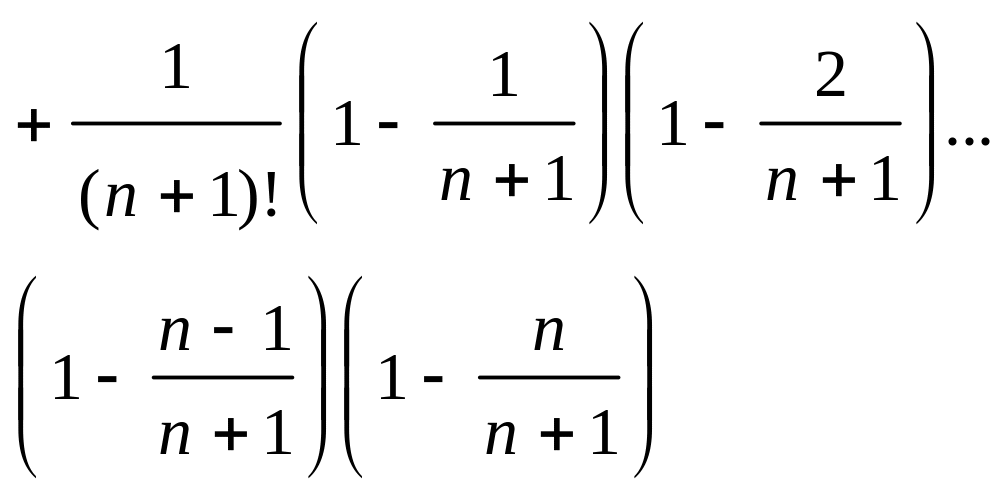(3)

Сравним выражения (2) и (3). Правая часть выражения (2) содержит положительное слагаемое, а выражения (3) положительных слагаемых. Причем каждое слагаемое вида в выражении (2) меньше аналогичного слагаемого в формуле (3). Следовательно, , и рассматриваемая последовательность возрастающая.

Докажем теперь ограниченность данной последовательности. Прежде всего, заметим, что при Следовательно, . Поскольку выражения вида меньше единицы при , то для справедливо неравенство

. (4)

Из выражения (2) и неравенства (4) следует неравенство

.

Используя формулу суммы членов геометрической прогрессии, имеем

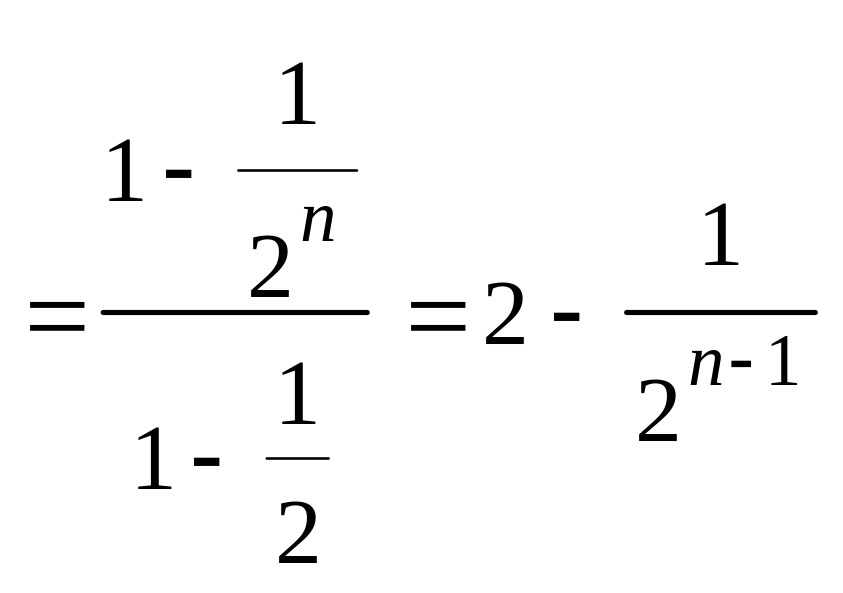
Тогда . Следовательно, последовательность ограничена сверху. Заметим также, что из формулы (2) следует, что

.

Мы доказали, что последовательность ограничена сверху и возрастает. По теореме Вейерштрасса она имеет предел. Этот предел называют числом , то есть

.

Поскольку , то , следовательно, число заключено в пределах от 2 до 3. Более точно, число равно 2,718281828459045…