Определение радиуса кривизны линзы и длины световой волны с помощью колец Ньютона

Приборы и принадлежности: стеклянная линза, смонтированная с плоской пластинкой; микроскоп; масштабная линейка с известной ценой деления; светофильтр, пропускающий свет известной длины волны; светофильтр, пропуска­ющий свет неизвестной длины волны.

Цель работы: определить радиус кривизны линзы и длину волны лазерного излучения с помощью колец Ньютона.

Теоретическое введение

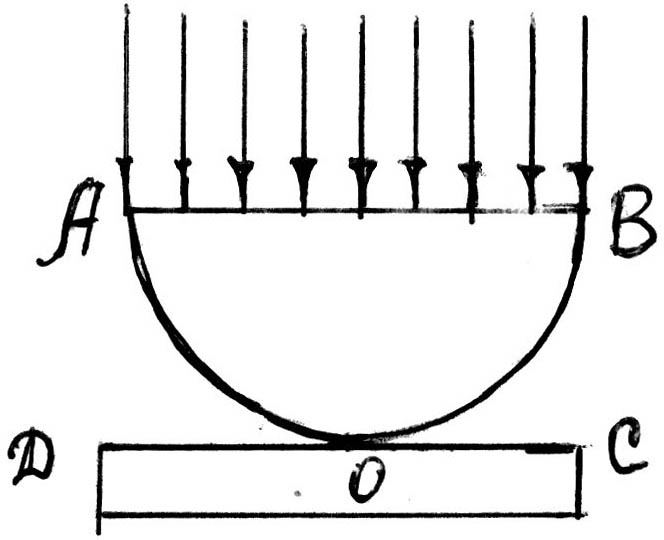
Классическим примером полос равной толщины являются кольца Ньютона. Если осветить монохроматическим светом плосковыпуклую линзу с большим радиусом малой кривизны, положенную сферической поверхностью на плоскую стеклянную пластину, то при наблюдении отраженного света будут видны кольца Ньютона (чередующиеся темные и светлые кольца с темным пятном в центре, рис. 1.6, 1.7). Кольца Ньютона являются результатом интерференции световых волн, одна из которых отражается от поверхности АОВ, другая - от поверхности DOC.

Т олщина воздушного слоя между этими поверхностями постепенно увеличивается по всем направлениям от точки их соприкос­новения, и полученные полосы равной толщины будут представлять собой концентрические окружности с центром в точке O.

Рис. 1.6

При отражении света от поверхности DОC (оптически более плотной среды) происходит потеря полуволны, поэтому оптическая разность хода между интерферирующими лучами

 = 2b + /2, (1.21)

где b - толщина зазора между сферической DОВ и плоской DОС поверхностями.

С учетом формул (1.21), (1.8), (1.9) получим следующие условия:

2b = (2k -1) /2 – (1.22)

максимум интенсивности отраженного света;

2b = 2k /2 – (1.23)

минимум интенсивности отраженного света,

где k - целое число.

С ледовательно, в тех местах, где удвоенная толщина воздушного зазора равна нечетному числу полуволн, в отраженном свете будут наблюдаться светлые кольца, а там, где удвоенная толщина воздушного зазора равна четному числу полуволн, - темные кольца.

Установим зависимость между радиусами наблюдаемых колец Ньютона r, толщиной воздушного слоя b и радиусом поверхности линзы R. На рис. 1.8 АOВ прямоугольный, его высота r есть среднегеометрическое между отрезками диаметра 2R - b и b, т.е.

, (1.24)

отсюда

r² = b (2R – b). (1.25)

Учитывая, что Rb, получим

R = r² / 2b. (1.26)

Поскольку для темного кольца (см. условие (1.23)),

R = r²_k / k . (1.27)

Зная радиус кривизны поверхности линзы, можно определить длину волны света, падающего на интерференционную систему. На основании условий (1.23) и (1.26) для k-гo и (k + m)-го колец можно записать

и (1.28)

.

Из этих равенств имеем

, (1.29)

где r_k, r_m+k – радиусы k-гo и ( k + m )-го темных колец.

Описание установки и порядок выполнения работы

Схема установки изображена на рис 1.9, где 1 - осветитель; 2 - светофильтр; 3 - окуляр микроскопа; 4 - объектив микроскопа; 5 - переключатель увеличения микроскопа; 6 - рукоятка фокусировки; 7 - предметный столик; 8 - линза, смонтированная с пластиной.

С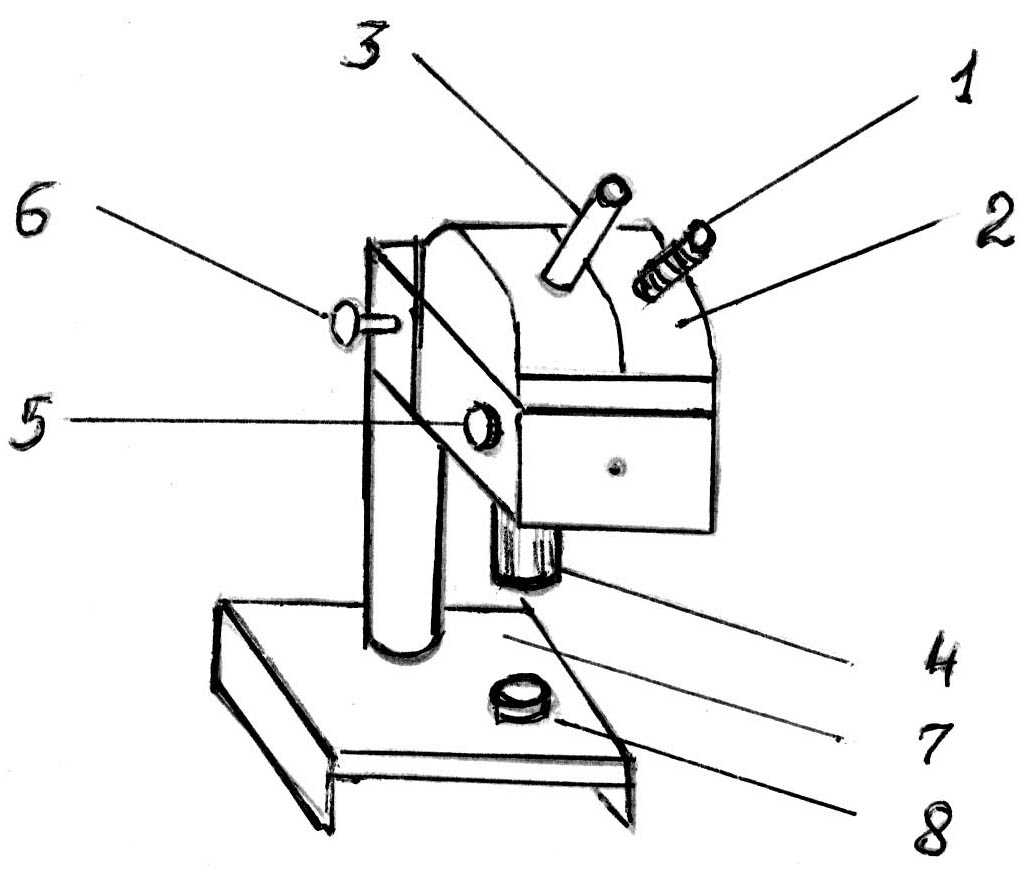 вет от лампы накаливания осветителя 1 проходит через светофильтр 2, падает вертикально на линзу, смонтированную с плоскопараллельной пластиной 8, и после отражения наблюдается через окуляр 3.

Рис. 1.9

Задание 1. Измерение радиуса колец Ньютона в делениях окулярной шкалы

1. Включить осветитель микроскопа 1.

2. Установить светофильтр 2 (= 546 нм).

3. Положить на столик микроскопа линзу.

4. Передвигая линзу, изменяя ручкой 5 увеличение микроскопа и фокусируя картину колец ручкой 6, получить резкое изображение колец Ньютона. Окулярная шкала при этом должна располагаться по диаметру колец.

5. И змерить координаты (по окулярной шкале) середин пересечения нескольких темных колец с окулярной шкалой, например, третьего и шестого колец (рис. 1.10).

6. Вычислить радиусы колец в делениях шкалы, например, для третьего кольца

.

7. Повторить указанные в пп.5 и 6 измерения и вычисления два раза. Определить среднее значение радиусов колец.

Задание 2. Определение цены деления окулярной шкалы

1. Поместить на столик микроскопа вместо линзы с пластинкой масштабную линейку, цена деления которой a₀ известна.

2. Добившись фокусировки при том же увеличении микроскопа, что и в задании 1, сравнить окулярную шкалу с масштабной и определить цену деления а окулярной шкалы. Для этого заметить, какое число m целых делений масштабной ли­нейки имеют такую же длину, как и n целых делений окулярной шкалы. Затем из равенства mа₀ = na вычислить

a = a₀ m / n.

3. Повторить указанные в п. 2 измерения два раза и определить среднее значение величины α .

Задание 3. Вычисление радиуса кривизны линзы и длины волны света

1. По формуле (1.27) вычислить значение радиуса кривизны линзы, используя данные о двух разных кольцах k-гo и (k + m)-гo порядков и учитывая, что r_k = r^*_k a:

; .

2. Найти среднее значение радиуса кривизны линзы.

3. Сменить светофильтр. Измерить радиусы k-го и (k + m)-гo колец Ньютона.

Используя полученное значение радиуса кривизны линзы по формуле (1.29), вычислить длину волны света, прошедшего через светофильтр.

Контрольные вопросы

Вариант 1

1. Какой свет называется монохроматическим, а какой когерентным?

2. Какое будет в центре пятно (светлое или темное) при наблюдении колец Ньютона в проходящем свете?

3. Выведите рабочую формулу для определения длины световой волны с помощью колец Ньютона.

4. Задача. Фронт волны желтого света прошел в стекле за некоторое время путь, равный 10 мм. Какой путь пройдет он за то же время в воде?

(n_ст= 1,50. n_в=1,33).

Ответ: l = 11,3 м.

Вариант 2

1. Перечислите методы получения когерентных волн.

2. Выведите рабочую формулу для расчета радиуса кривизны линзы.

3. В чем состоит "просветление" оптики?

4. Задача. Длина волны желтого света в воздухе равна 5890 Å. Какова длина волны этого света в воде (n_в = 1,33) и в стекле (n_ст = 1,50)?

Ответ: ₁ = 143 нм; ₂ = 393 нм.

Вариант 3

1. Объясните природу радужной окраски некоторых поверхностей (мыльного пузыря, металла, крылышек насекомых).

2. Нарисуйте схему опытов для наблюдения полос равной толщины.

3. Выведите условия интерференционных максимумов и минимумов.

4. Задача. Плосковыпуклая линза выпуклой стороной лежит на стеклянной пластике. Определить толщину слоя воздуха в том месте, где в отраженном свете ( = 0,6 мкм) видно первое светлое кольцо Ньютона.

Ответ: b = 0,15 мкм.

Лабораторная работа № 3-03