21

1. Интерференция света

Интерференция волн – явление усиления или ослабления амплитуды результирующей волны в зависимости от соотношения между фазами накладывающихся в пространстве двух (или нескольких) волн с одинаковыми периодами. Интерференция имеет место для всяких волн независимо от их природы (упругих, электромагнитных и др.). Она может наблюдаться только при выполнении условия когерентности накладывающихся волн. Волны являются когерентными, если они имеют одинаковую частоту и разность фаз между ними в какой-либо точке пространства не меняется во времени.

Когда в пространстве распространяются две волны, то в случае, если среда, в которой они распространяются, линейна (т.е. отсутствует зависимость свойств среды от интенсивности волны), соблюдается принцип суперпозиции и результирующее колебание представляет собой сумму колебаний, соответствующих каждой из накладывающихся волн.

Р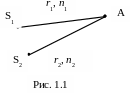 ассмотрим простейший пример наложения двух когерентных световых волн, распространяющихся от источников S₁ и S₂. Предположим, что пространство между источником S₁ и точкой А заполнено средой с показателем преломления n₁, а пространство между источником S₂ и точкой А - средой с показателем преломления n₂ (соответствующие геометрические расстояния между точкой А и источниками S₁ и S₂ равны r ₁ и r₂, рис. 1.1). Уравнения накладывающихся бегущих волн в точке А имеют вид

E₁ = E₁₀ cos ω (t – τ₁) ; E₂ = E₂₀ cos ω (t – τ₂) , (1.1)

где E₁₀ и Е₂₀ –амплитуды накладывающихся колебаний; τ₁ и τ₂ – время распространения колебаний от источников S₁ и S₂ до точки наблюдения А.

Если υ₁ и υ₂ – скорости распространения волн в первой и во второй среде, то

; .

С учетом этого формулы (1.1) приобретут вид:

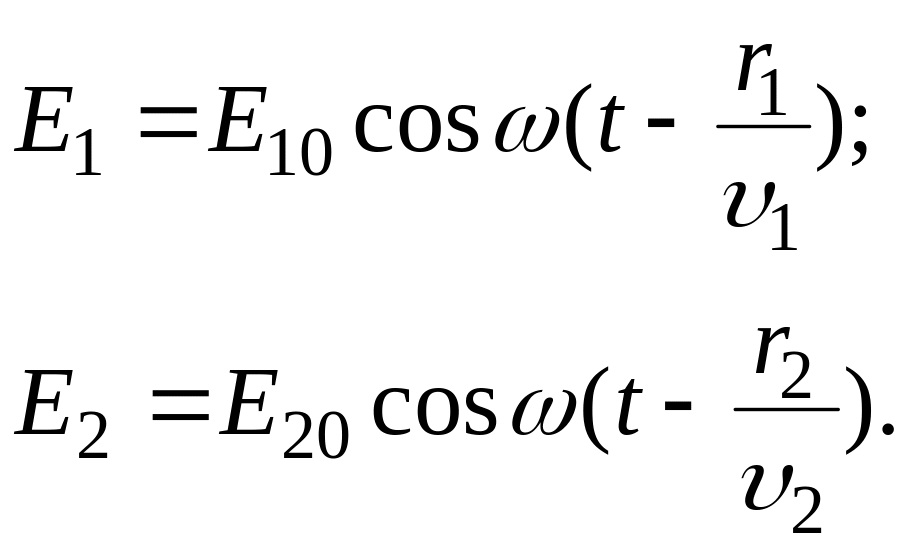(1.2)

А мплитуду результирующего колебания найдем графическим методом. На рис. 1.2 изображена векторная диаграмма сложения двух колебаний с амплитудами Е₁₀ и Е₂₀.

Амплитуда результирующего колебания

Е₀ = , (1.3)

где .

Поскольку плотность потока энергии волны j пропорциональна квадрату ее амплитуды, то результирующая плотность потока энергии (интенсивность)

. (1.4)

Разность фаз взаимодействующих волн может быть выражена через длину волны излучения в вакууме λ₀, геометрические (r₁ и r₂) и оптические (n₁ и n₂) параметры сред. Учитывая, что

; ; , (1.5)

имеем

. (1.6)

Величины n₁r₁ и n₂r₂ называются оптическими длинами путей, а их разность

Δ = n₁r₁ –n₂r₂ – (1.7)

оптической разностью хода.

Из соотношения (1.4) видно, что при наложении волн, создаваемых когерентными источниками света, результирующая интенсивность не равна сумме интенсивностей, создаваемых отдельными источниками. Максимальная интенсивность наблюдается в точках, для которых выполняется условие соs φ = 1, минимальная - при соs φ = -1. Таким образом, условие усиления волны имеет вид

, или , (1.8)

условие ослабления —

, или , (1.9)

где m — целое число.

Соотношения (1.8) и (1.9) показывают, что максимальной освещенности соответствует оптическая разность хода лучей, равная четному числу полуволн, а минимальной - разность хода лучей, равная нечетному числу полуволн. Величина k определяет порядок мак­симума и минимума и принимает значения 0, 1, 2,... . В результате интерференции на экране возникает совокупность светлых и темных полос. При интерференции усиление освещенности в одних местах происходит за счет ее ослабления, в других - согласно закону сохранения энергии.

При оптической разности хода , cos φ = 1 и в соответствии с формулой (1.4)

I = I₁ + I₂ + 2 ,

а при оптической разности хода

;

.

Если интенсивности накладывающихся волн равны (I₁ = I₂ = I₀), максимуму интенсивности соответствует I = 4I₀, а минимуму –I=0.

В этом случае интерференционная картина будет наиболее четкая.

Естественные источники света не являются когерентными. Это обусловлено тем, что излучение светящегося тела слагается из волн, испускаемых многими атомами. Отдельные атомы излучают цуги волн длительностью 10^-8 с. Фаза нового цуга волн никак не связана с фазой предыдущего цуга, а также с фазами цугов волн других атомов. В испускаемой телом световой волне излучение одной группы атомов сменяется излучением другой группы атомов, а разность фаз между слагающимися волнами является случайной величиной. При этом происходит простое суммирование интенсивностей взаимодействующих волн, не приводящее к перераспределению энергии в про­странстве.

Если условие когерентности волн выполняется, то в пространстве получается некоторое неизменное распределение амплитуд результирующей волны с чередующимися максимумами и минимумами.

Когерентные световые волны можно получить путем деления волны, испускаемой каким-либо источником света, на две волны, разность фаз между которыми зависит от оптической разности хода и не изменяется во времени. При этом разность хода не должна быть большой, так как интерферирующие волны должны принадлежать одно­му и тому же цугу волн. Если это условие нарушается, то разность фаз между ними будет изменяться с течением времени.

Интерференцию света можно наблюдать, используя зеркала Френеля, или бипризму Френеля, или щели Юнга.

В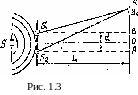 методе Юнга источником света служит щель S, от которой цилиндрическая световая волна падает на две узкие параллельные щели S₁ и S₂ (рис. 1.3). Таким образом, щели освещаются различными участками одной и той же волновой поверхности и на основании прин­ципа Гюйгенса –Френеля они являются источниками вторичных когерентных волн. Рассмотрим волны, которые распространяются вдоль направлений S₁M и S₂М и взаимодействуют на экране, удаленном от плоскости щелей на расстояние L » d (d - рас­стояние между щелями). Оптическая разность хода этих волн

Δ = S₂M - S₁М (n₁= n₂ = 1).

Из треугольников S₁MВ и S₁MА следует, что

S₁M² = L² +(y_m – d/2)² ;

S₂M² = L² +(y_m + d/2)² ,

откуда (S₁M + S₂M)(S₂M - S₁M) = 2y_md.

Поскольку L  d, S₁M + S₂M ≈ 2L,

то .

Максимальная освещенность наблюдается при выполнении условия (1.8). Этому условию соответствуют значения y_m ,удовлетворяющие соотношению

. (1.10)

Расстояние между соседними максимумами (минимумами)

. (1.11)

Оно тем больше , чем сильнее неравенство L  d.

Если щели S₁ и S₂ освещены белым светом, то интерференционная картина имеет следующий вид. В центре картины расположен максимум нулевого порядка, окрашенный в белый цвет. По обе стороны от него находятся спектры первого и высших порядков (m  1). В спектре каждого порядка ближайший к центру край окрашен в фиолетовый цвет, удаленный - в красный. В спектрах высших порядков (m > 3) наблюдается наложение максимумов разных длин волн и разных порядков, поэтому интерференционная картина размывается.

Лабораторная работа № 3-01