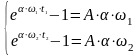4. Ползучесть древесины

При кратковременном действии нагрузки древесина работает практически упруго, но при длительном действии неизменной нагрузки деформации во времени увеличиваются. Даже при малом уровне напряжений ползучесть может продолжаться годами. С увеличением уровня напряжений ползучесть проявляется более ярко и может привести к разрушению конструкции. Отслеживанием деформаций ползучести, путем замера прогибов можно прогнозировать эксплуатационное состояние деревянных конструкций.

Но если для деревянных конструкций ползучесть является недостатком, то в отдельных случаях при изготовлении изделий из древесины это свойство может обернуться достоинством, например, необходимо придать изделию криволинейную форму.

При длительных нагрузках к упругим деформациям добавляются еще зависящие от времени пластические деформации; у решетчатых ферм к таким деформациям ведут дополнительные сдвиги стыковых соединений.

П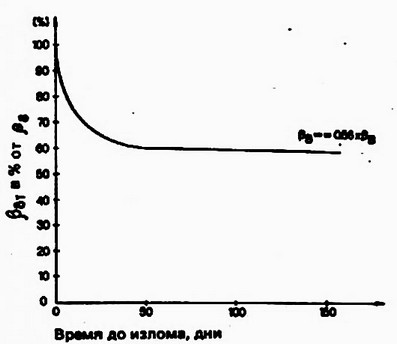 олзучесть - это увеличение деформации при неизменной нагрузке. Кривые деформации во времени показаны на рис. 41. Можно заметить, что деформации в зависимости от напряжения спустя некоторый отрезок времени достигают определенных величин, которые при допускаемых напряжениях превышают упругую деформацию примерно в 1,6-2 раза (кривая l), но при более высоких напряжениях, превышающих так называемый предел ползучести, деформации через некоторое время начинают ускоренно возрастать, что, наконец, приводит к излому стержня (кривая 2). Если после неограниченно долгого времени излом не происходит, то это характеризует состояние длительной прочности. У большинства видов древесины пределы ползучести и длительной прочности совпадают; для древесины без пороков эта величина составляет

41 - Кривые ползучести балок, работающих на изгиб

42 - Кривые сопротивления ползучести хвойной древесины

примерно от 50 до 60% статической прочности (рис. 42). Законы ползучести, в первую очередь влияние изменения влажности, снятия и чередования нагрузок, еще недостаточно изучены. Поэтому ползучесть математически может быть выражена только приблизительно.

После установления экспериментальным путем величины удлинения от ползучести Ekрассчитывается общее удлинение

Поскольку Eel = Q/Е, то

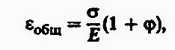
откуда находят модуль деформации Eф, включающий длительную деформацию:

По имеющимся в настоящее время экспериментальным данным при длительной нагрузке до допустимого напряжения величина принимает значения от 0,6 до 1. Если при расчете по допускаемым напряжениям, установленным с более чем трехкратным запасом по отношению к статической прочности, учитывается и длительная прочность при статической нагрузке, то при расчетах деформаций влияние ползучести приближенно оценивается снижением модуля упругости. Коэффициент снижения n может приниматься равным:

5. Длительная прочность древесины

На прочность древесины благодаря ее реологическим свойствам значительно влияют скорость приложения нагрузки или продолжительность ее действия. Если серию одинаковых деревянных образцов загрузить, например на изгиб, различной по значению постоянной нагрузкой, то разрушение их произойдет через разные промежутки времени – чем больше нагрузка, тем быстрее разрушится образец. Представив результаты этих испытаний в виде графика, получим асимптотическую кривую, по которой можно определить, сколько времени пройдет от начала загружения до момента разрушения. Асимптотический характер кривой показывает, что предел прочности падает с увеличение длительности действия нагрузки, но не безгранично – он стремится к некоторой постоянной величине _дл равному ординате асимптоты кривой. Длительное сопротивление характеризует такое значение нагрузки, пр котором древесина не разрушится как бы долго ни была приложена нагрузка.

Кривые деформации во времени: а – при  < _дл; б – при  > _дл.

К

Кривая длительного сопротивления древесины.

оэффициент длительного сопротивления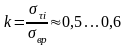

При изменении температуры (базовая – 20⁰ С) кривая длительного сопротивления перемещается вдоль оси ординат параллельно исходной: вверх – при уменьшении температуры, вниз – при увеличении температуры древесины.

Температурный коэффициент временной прочности

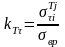
Длительное сопротивление является показателем действительной прочности древесины в отличие от предела прочности, определяемого быстрыми испытаниями на машине. Переход от предела прочности к длительному сопротивлению производится умножением предела прочности _вр на вышеперечисленные коэффициенты.

При напряжениях меньших _дл деформации с течением времени затухают, стремясь к некоторому пределу как показано на рисунке. При обратной ситуации после некоторого уменьшения скорости деформаций на участке в-г наступает развитие деформаций с постоянной скоростью на участке г-д. Далее в момент времени t₁ начинается ускоренный рост деформаций, приводящий к разрушению материала.

Кривая длительной сопротивления задается уравнением:

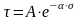
Процесс разрушения древесины при выдерживании ее под действием различных по величине нагрузок с различным временем выдержки начинается при условии, что:

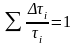
Где: _I – время длительности i загружения, долговечность этого материала при i нагрузке;

Если принять линейный закон загружения 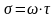, то: