12. Взаимная индукция. Трансформаторы

Р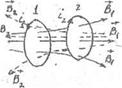 ассмотрим два неподвижных контура (1 и 2), расположенных достаточно близко друг от друга. Если в контуре 1 течет ток I₁, то магнитный поток, создаваемый этим током пропорционален I₁. Обозначим через Ф₂₁ ту часть потока, которая пронизывает контур 2. Тогда

где L₂₁ - коэффициент пропорциональности.

Если ток I₁ изменяется, то в контуре 2 индуцируется ЭДС ?_i2

Аналогично, при протекании в контуре 2 тока I₂ магнитный поток пронизывает контур 1 - Ф₁₂

Если I₂ изменяется, то

Явление возникновения ЭДС в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности L₁₂ иL₂₁ называются взаимной индуктивностью контуров.

L₁₂ = L₂₁.

L₁₂ и L₂₁ зависят от геометрической формы, размеров, взаимного расположения контуров и от магнитной проницаемости окружающей контуры среды.

[L₁₂] =Гн.

Рассчитаем взаимную индуктивность двух катушек, намотанных на общий тороидальный сердечник. Магнитная индукция поля, создаваемого катушкой 1 с числом витковN₁, магнитной проницаемость µ сердечника:

где   -длина сердечника по средней линии

Магнитный поток через один виток катушки 2:

Полный магнитный поток:

Следовательно,

1. Трансформаторы (преобразователи) - устройства для повышения, понижения, гальванической развязки и др. напряжения и тока.

Принцип действия основан на явлении взаимной индукции. Первичная

и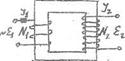 вторичная обмотки, имеющие N₁ и N₂ витков соответственно, укреплены на замкнутом железном сердечнике. Изменение потока в обмотке 1, подключенной к переменной ЭДС, вызывает во вторичной обмотке появление ЭДС взаимной индукции, а в первичной - ЭДС самоиндукции.

Ток I₁ первичной обмотки определяется по закону Ома

R₁ - сопротивление первичной обмотки,

I₁R₁ мало по сравнении   и   в переменных полях. Следовательно,

ЭДС взаимной индукции во вторичной обмотке

 Следовательно,

Знак “ - “означает, что фазы   и  противоположны.

 - коэффициент трансформации.

k > 1- повышающий трансформатор;

k < 1- понижающий трансформатор.

Следовательно, токи в обмотках обратно пропорциональны числу витков в этих обмотках.

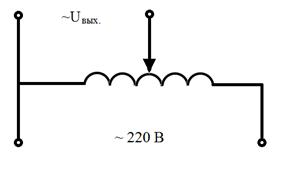
Трансформатор, состоящий из одной обмотки, называется автотрансформатором.

 

 

 

13. Проводник, c протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля.  Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI. Но для изменения магнитного потока на величину dФ следует совершить работу dА=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф равна    Значит, энергия магнитного поля, которое связано с контуром,   (1)  Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (1) формулу индуктивности соленоида, найдем    Так как I=Bl/(μ₀μN) и В=μ₀μH , то   (2)  где Sl = V — объем соленоида.  Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия (2) заключена в объеме соленоида и имеет с нем однородное распределение с постоянной объемной плотностью   (3)  Формула (3) для объемной плотности энергии магнитного поля имеет вид, аналогичный выражению для объемной плотности энергии электростатического поля, с тем отличием, что электрические величины заменены в нем магнитными. Формула (3) выводилась для однородного поля, но она верна и для неоднородных полей. Формула (3) справедлива только для сред, для которых линейная зависимость В от Н , т.е. оно относится только к пара- и диамагнетикам. объемная плотность энергии) — энергия, связанная с магнитным полем и преобразующаяся в другие формы энергии при изменении магнитного поля. Энергия магнитного поля равна работе, которая затрачивается на создание этого поля. Согласно теории близкодействия, энергия магнитного поля (как и энергия электрического поля) распределена по всему объему V пространства, в котором существует магнитное поле. Величина Wm, равная энергии магнитного поля, заключенной в единичном объеме этого поля, называется объемной плотностью энергии магнитного поля.

Ее можно рассчитать по формуле: Wm = В²/2 μ μ0, где

В — модуль индукции магнитного поля,

μ — магнитная проницаемость среды,

μ0 — магнитная постоянная.

Измеряется в Дж/м³ или МГсЭ (Мега Гаусс Эрстеды). Например, максимальная энергия магнитного поля неодимовых магнитов составляет 278-360 кДж/м³, а ферритовых до 30 кДж/м³. Это означает, чтобы обеспечить одну и ту же величину магнитного потока, объем магнитного материла ферритов потребуется в несколько раз больший, чем магнитного материала NdFeB.

Чем сильнее величина энергии магнитного поля, тем более мощный магнит еей обладает.

14.Дифференциальная форма уравнений Максвелла.

1. Применяя теорему Стокса, преобразуем левую часть первого уравнения Максвелла к виду:  .

 Тогда само уравнение можно переписать как  , откуда, в силу произвольности поверхности интегрирования, имеем:

2. Применяя теорему Остроградского ко второму уравнению Максвелла, находим:

,

откуда, в силу произвольности объема интегрирования, имеем:

3. Применяя теорему Стокса, преобразуем левую часть третьего уравнения Максвелла к виду:

.

Тогда само уравнение можно переписать как  , откуда, в силу произвольности поверхности интегрирования, имеем:

4. Применяя теорему Остроградского, преобразуем левую часть четвертого уравнения Максвелла к виду:

.

Тогда само уравнение можно переписать как  , откуда, в силу произвольности объема интегрирования, имеем:

Замкнутая система уравнений Максвелла. Материальные уравнения.

Для замыкания системы уравнений Максвелла необходимо еще указать связь между векторами  ,  ,   и  , то есть конкретизировать свойства материальной среды, в которой рассматривается электромагнитное поле. Если эти соотношения известны (они называются материальными уравнениями), то по заданному распределению зарядов ρ и токов  однозначно находится распределение электрических и магнитных полей в данной среде; или по заданному распределению полей находится распределение зарядов и токов. Для однородной изотропной среды материальные уравнения записывают обычно в виде:

 ;  .

Если среда не обладает сегнетоэлектрическими или ферромагнитными свойствами, то   и  . В этом случае материальные уравнения имеют наиболее простой вид:

 ; 

(в частности, для вакуума  , тогда   и  ).

Следует подчеркнуть, что написанные соотношения справедливы только для неподвижных сред. В движущихся средах они имеют более сложный вид, обусловленный требованиями релятивистской инвариантности уравнений Максвелла.

 Таблица 2. Замкнутая система уравнений Максвелла.

Интегральная форма	Дифференциальная форма
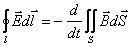
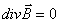
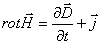
Материальные уравнения

Следствия из уравнений Максвелла. Электромагнитные волны. Скорость света.

Рассмотрим некоторые основные следствия, вытекающие из уравнений Максвелла, приведенных в таблице 2. Прежде всего, отметим, что эти уравнения линейные. Отсюда следует, что электромагнитное поле удовлетворяют принципу суперпозиции.

Одним из главных следствий, вытекающих из уравнений Максвелла, является то, что электромагнитное поле может существовать в виде электромагнитных волн в отсутствие всяких зарядов и токов ( ).

В этом случае уравнения Максвелла принимают вид (в дифференциальной форме):

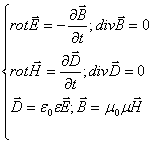
Применяя к первому из этих уравнений операцию  , будем иметь:

.

Но согласно третьему уравнению (с учетом материальных уравнений):  . Используя это соотношение, получим:

.

Далее, принимая во внимание, что  , причем в силу четвертого уравнения  , приходим к так называемому волновому уравнению для электрического поля :

где обозначено   - оператор Лапласа (в декартовых координатах).

Аналогичное волновое уравнение получается для магнитного поля  :

 

Совместным решением этих уравнений является векторная волновая функция электромагнитного поля:

,  .

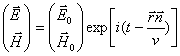Коэффициент   имеет смысл фазовой скорости электромагнитной волны (см. Лекцию 17):

Для вакуума:  . Тогда:  м/c, что совпадает со скоростью света в вакууме с. Таким образом, мы приходим к выводу, что свет – это электромагнитная волна.

В прозрачной диэлектрической среде скорость света

где величина   называется показателем преломления среды. Для многих оптически прозрачных сред эта формула дает хорошие совпадения с измеренными на опыте значениями n, что также является одним из достижений теории Максвелла.

Некоторые другие следствия, вытекающие из волновой теории электромагнитного поля, рассматриваются в Лекции17.

Магнитное поле Действие магнитного поля на движущий ся заряд. Сила Лоренца. Явление самоиндукции и взаимной индукции. Энергия системы проводников с током. Объемная плотность энергии магнитного поля. Постоянный электрический ток Закон Ома в дифференциальной форме. Разность потенциалов, электродвижущая сила, напряжение. Работа и мощность тока.

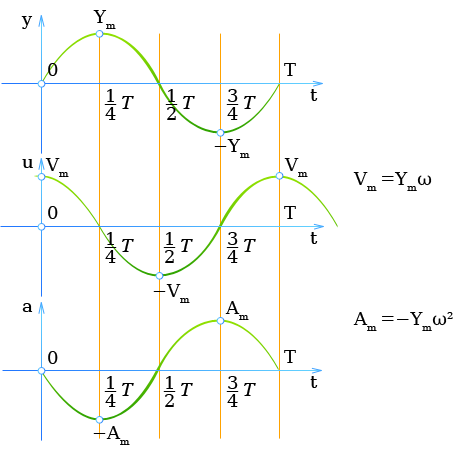
15. Незатухающие гармонические колебания можно представить в виде проекции равномерного движения по окружности. Если изобразить графически колебания на диаграмме отклонение — время, то получитсясинусоидальная кривая. Поэтому часто гармонические колебания называются также синусоидальными колебаниями.

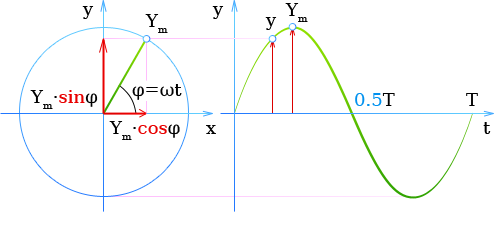
Незатухающие гармонические колебания

При прохождении положения равновесия, т. е. положения, которое занимает покоящаяся система, колеблющееся тело имеет наибольшую скорость. В точке максимального отклонения (точке поворота) скорость равна нулю.