Электродвижущая сила самоиндукции

Электродвижущая сила самоиндукции зависит от изменений силы тока, питающего проводник, так как она является следствием изменений магнитного потока сквозь контур проводника, вызываемых изменениями силы тока, текущего в нём.

Электродвижущую силу самоиндукции, индуктирующуюся в проводнике при возрастании силы тока на 1 ампер в 1 секунду, называют коэффициентом самоиндукции.

Коэффициент самоиндукций определяется также, как изменение магнитного потока сквозь контур проводника, при изменении силы тока на 1 ампер в 1 сек. то есть

.

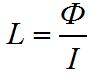Единица коэффициента самоиндукции по величине соответствует самоиндукции такого проводника, в котором появляется электродвижущая сила самоиндукции в 1 вольт при изменении силы тока на 1 ампер в 1 секунду. Эта единица носит название генри.

Взаимодействие между током и магнитным полем

Силовые линии, окружающие проводник, по которому течёт ток, взаимодействуют с силовыми линиями магнитного поля, в которое будет помещён проводник так, что проводник получает стремление к перемещению перпендикулярно к силовым линиям поля, и таким образом получается превращение электрической энергии (тока) в механическую энергию (движение).

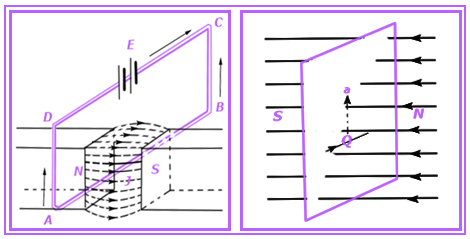
Сила взаимодействия F между проводником, по которому течёт ток, и магнитным полем, в котором проводник находится, на основании закона Био и Савара будет тем больше, чем больше магнитная индукция – В, чем больше сила тока I, текущего по проводнику, и чем больше длина проводника l, и именно, когда проводник перпендикулярен к магнитным силовым линиям:

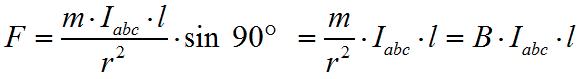
Если проводник длиною в 1 см, по которому течёт ток, будет помещен в магнитное поле с напряжением, равным 1, и если сила взаимодействия проводника и магнитного поля при этом окажется равной 1 дине (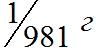 ) то по проводнику будет течь вполне определённый ток (абсолютная единица силы тока), сила которого в 10 раз больше ампера.

Поэтому можно написать

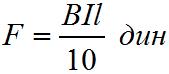
то есть сила взаимодействия F в динах между проводником, несущим ток, и магнитным полем равна одной десятой доле произведения магнитной индукции В на силу тока I, текущего по проводнику, в амперах и на длину проводника l в сантиметрах.

Направление движения проводника, несущего ток, под влиянием магнитного поля легко может быть определено из закона взаимодействия силовых линий. Так, например, проводник, изображенный справа, принужден будет начать двигаться вниз ввиду того, что силовые линии, окружающие его, встречаясь с силовыми линиями магнитного поля, в котором они находятся, в верхней своей части производят отталкивание, а в нижней своей части притяжение, благодаря чему получается общее стремление проводника книзу. При перемене направления тока в проводнике получается взаимодействие силовых линий, стремящееся перемещать проводник вверх.

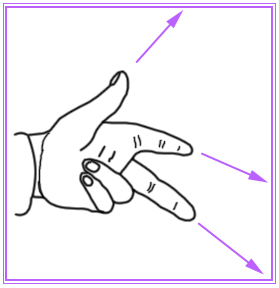
Направление движения проводника в магнитном поле под влиянием взаимодействия силовых линий может быть найдено проще, пользуясь правилом левой руки, согласно которому следует левую руку расположить ладонью к северному полюсу, направив вытянутые пальцы по течению тока в проводнике, тогда отставленный большой палец укажет направление движения проводника.

В какую сторону (вверх или вниз) будет иметь стремление двигаться проводчик, несущий ток, направленный от нас, если проводник находится перед северным полюсом магнита, расположенного от нас слева?

Согласно правилу левой руки ладонь её располагаем к северному полюсу и вытянутые пальцы в направлении течения тока в проводнике; тогда отставленный большой палец будет показывать на направление движения проводника вниз.

В какую сторону будет двигаться тот же проводник, если ток в нём переменить на обратный?

Проводник, согласно правилу левой руки, будет двигаться вверх.

С тою же целью пользуются правилом Флемминга, для чего располагают большой, указательный и средний пальцы левой руки по взаимно перпендикулярным направлениям, причём указательный – в направлении тока, средний – в направлении силовых линий, тогда большой палец укажет искомое направление перемещения проводника.

В контуре, несущем ток и перемещающемся под влиянием этого тока в магнитном поле, помимо основного тока появляется вообще ток индуктированный, так как магнитный поток сквозь контур может изменяться.

Согласно правилу правой руки направление индуктированного в этом случае тока будет обратно основному току, почему электродвижущая сила, вызывающая его, носит название обратной электродвижущей силы.

Наличность обратной электродвижущей силы ослабляет силу основного тока в проводнике, которая, если бы не было обратной электродвижущей силы, имела бы величину

,

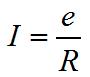где е – напряжение у зажимов проводника, a R – сопротивление проводника. При наличности же обратной электродвижущей силы Е₀, сила тока в проводнике будет иметь величину меньшую, а именно:

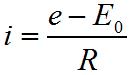
Проводник, питаемый током с напряжением в 125 вольт, пришел в движение со скоростью 10 м/сек. Необходимо определить величину обратной электродвижущей силы, индуктирующейся в нём при этом, если магнитная индукция равна 15000 единиц, а полезная длина проводника, участвующая в изменении магнитного потока сквозь контур, замыкающий проводник, 750 см.

Величина обратной электродвижущей силы будет найдена из общей формулы индуктированной электродвижущей силы

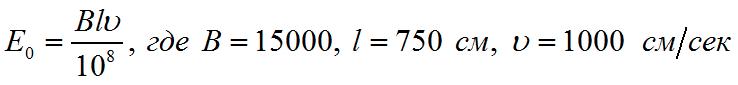
Следовательно 

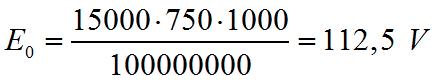
Токи при замыкании и размыкании цепи, содержащей индуктивность

    По правилу Ленца дополнительные токи, возникающие в проводниках вследствие самоиндукции, всегда направлены так, чтобы воспрепятствовать изменениям тока, текущего в цепи. Это приводит к тому, что установление тока при замыкании цепи и убывание тока при размыкании цепи происходит не мгновенно, а постепенно.

Сначала найдем характер изменения тока при размыкании цепи (рис. 3).   

Рис. 3

Пусть в цепь с независящей от I индуктивностью L и сопротивлением Rвключен источник тока, имеющий ЭДС  . Под действием этой ЭДС в цепи будет течь постоянный ток: . В момент времени t=0 отключим ЭДС, переведем переключатель П в положение 2. Как только сила тока в цепи станет убывать возникает ЭДС самоиндукции. Закон Ома:

IR= =L .

Перепишем это выражение следующим образом:

.

Это линейное однородное дифференциальное уравнение 1-го порядка. Его легко проинтегрировать, разделив переменные:

, откуда  .

Потенцирование этого соотношения дает:

.

Это выражение является общим решением дифференциального уравнения первого порядка. При t=0, сила тока равна:

, следовательно, const = I₀,

тогда  .

    Отсюда видно, что сила тока убывает по экспоненте (рис. 4).

Рассмотрим случай замыкания цепи. После подключения к источнику тока до тех пор, пока сила тока не примет установившегося значения, в цепи кроме ЭДС   будет действовать ЭДС самоиндукции.     В соответствии с законом Ома можно написать, что IR= + = -L .

    После преобразования приходим к линейному неоднородному уравнению:

.

    Общее решение этого уравнения можно получить, прибавив любое его частное решение к общему решению однородного уравнения.

.

В момент времени t=0, I=0. Отсюда, для сonst получается значение сonst = -I₀.

То есть  , (см. рис. 4).

    Если цепь содержит катушку с железным сердечником, ЭДС самоиндукции будет определяться

.

    В этом случае за счет слагаемого   ЭДС самоиндукции может достигать очень больших значений, и сила тока может значительно превзойтиI₀.