1.Магнитное Поле

Если два параллельно расположенных проводника подсоединить к источнику тока так, чтобы по ним прошел электрический ток, то в зависимости от направления тока в них проводники либо отталкиваются, либо притягиваются.

Объяснение этого явления возможно с позиции возникновения вокруг проводников особого вида материи - магнитного поля.

Силы, с которыми взаимодействуют проводники с током, называются магнитными.

Магнитное поле - это особый вид материи, специфической особенностью которой является действие на движущийся электрический заряд, проводники с током, тела, обладающие магнитным моментом, с силой, зависящей от вектора скорости заряда, направления силы тока в проводнике и от направления магнитного момента тела.

История магнетизма уходит корнями в глубокую древность, к античным цивилизациям Малой Азии. Именно на территории Малой Азии, в Магнезии, находили горную породу, образцы которой притягивались друг к другу. По названию местности такие образцы и стали называть "магнетиками". Любой магнит в форме стержня или подковы имеет два торца, которые называются полюсами; именно в этом месте сильнее всего и проявляются его магнитные свойства. Если подвесить магнит на нитке, один полюс всегда будет указывать на север. На этом принципе основан компас. Обращенный на север полюс свободно висящего магнита называется северным полюсом магнита (N). Противоположный полюс называется южным полюсом (S).

Магнитные полюсы взаимодействуют друг с другом: одноименные полюсы отталкиваются, а разноименные - притягиваются. Аналогично концепции электрического поля, окружающего электрический заряд, вводят представление о магнитном поле вокруг магнита.

В 1820 г. Эрстед (1777-1851) обнаружил, что магнитная стрелка, расположенная рядом с электрическим проводником, отклоняется, когда по проводнику течет ток, т. е. вокруг проводника с током создается магнитное поле. Если взять рамку с током, то внешнее магнитное поле взаимодействует с магнитным полем рамки и оказывает на нее ориентирующее действие, т. е. существует такое положение рамки, при котором внешнее магнитное поле оказывает на нее максимальное вращающее действие, и существует положение, когда вращающий момент сил равен нулю.

Магнитное поле в любой точке можно охарактеризовать вектором В, который называется вектором магнитной индукции илимагнитной индукцией в точке.

Магнитная индукция В - это векторная физическая величина, являющаяся силовой характеристикой магнитного поля в точке. Она равна отношению максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на ее площадь:

За направление вектора магнитной индукции В принимается направление положительной нормали к рамке, которое связано с током в рамке правилом правого винта, при механическом моменте, равном нулю.

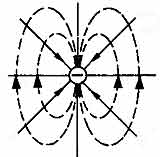
Точно так же, как изображали линии напряженности электрического поля, изображают линии индукции магнитного поля. Линия индукции магнитного поля - воображаемая линия, касательная к которой совпадает с направлением В в точке.

Направления магнитного поля в данной точке можно определить еще как направление, которое указывает

северный полюс стрелки компаса, помещенный в эту точку. Считают, что линии индукции магнитного поля направлены от северного полюса к южному.

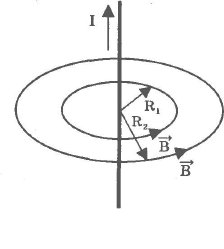
Направление линий магнитной индукции магнитного поля, созданного электрическим током, который течет по прямолинейному проводнику, определяется правилом буравчика или правого винта. За направление линий магнитной индукции принимается направление вращения головки винта, которое обеспечивало бы поступательное его движение по направлению электрического тока (рис. 59).

где n₀₁= 4Пи• 10^-7В • с/(А • м). - магнитная постоянная, R - расстояние, I - сила тока в проводнике.

В отличие от линий напряженности электростатического поля, которые начинаются на положительном заряде и оканчиваются на отрицательном, линии индукции магнитного поля всегда замкнуты. Магнитного заряда аналогично электрическому заряду не обнаружено.

За единицу индукции принимается одна тесла (1 Тл) - индукция такого однородного магнитного поля, в котором на рамку площадью 1 м², по которой течет ток в 1 А, действует максимальный вращающий механический момент сил, равный 1 Н • м.

Индукцию магнитного поля можно определить и по силе, действующей на проводник с током в магнитном поле.

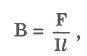
На проводник с током, помещенный в магнитное поле, действует сила Ампера, величина которой определяется следующим выражением:

где I - сила тока в проводнике, l -длина проводника, В - модуль вектора магнитной индукции, а - угол между вектором и направлением тока.

Направление силы Ампера можно определить по правилу левой руки: ладонь левой руки располагаем так, чтобы линии магнитной индукции входили в ладонь, четыре пальца располагаем по направлению тока в проводнике, то отогнутый большой палец показывает направление силы Ампера.

Учитывая, что I = q₀nSv, и подставляя это выражение в (3.21), получим F = q₀nSh/B sin a. Число частиц (N) в заданном объеме проводника равно N = nSl, тогда F = q₀NvB sin a.

Определим силу, действующую со стороны магнитного поля на отдельную заряженную частицу, движущуюся в магнитном поле:

Эту силу называют силой Лоренца (1853-1928). Направление силы Лоренца можно определить по правилу левой руки: ладонь левой руки располагаем так, чтобы линии магнитной индукции входили в ладонь, четыре пальца показывали направление движения положительного заряда, большой отогнутый палец покажет направление силы Лоренца.

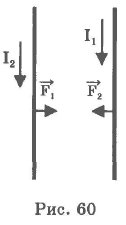
Сила взаимодействия между двумя параллельными проводниками, по которым текут токи I₁ и I₂ равна:

где l -часть проводника, находящаяся в магнитном поле. Если токи одного направления, то проводники притягиваются (рис. 60), если противоположного направления - отталкиваются. Силы, действующие на каждый проводник, равны по модулю, противоположны по направлению. Формула (3.22) является основной для определения единицы силы тока 1 ампер (1 А).

Магнитные свойства вещества характеризует скалярная физическая величина - магнитная проницаемость, показывающая во сколько раз индукция В магнитного поля в веществе, полностью заполняющем поле, отличается по модулю от индукции В₀магнитного поля в вакууме:

По своим магнитным свойствам все вещества делятся на диамагнитные, парамагнитные и ферромагнитные.

Рассмотрим природу магнитных свойств веществ.

Электроны в оболочке атомов вещества движутся по различным орбитам. Для упрощения считаем эти орбиты круговыми, и каждый электрон, обращающийся вокруг атомного ядра, можно рассматривать как круговой электрический ток. Каждый электрон, как круговой ток, создает магнитное поле, которое назовем орбитальным. Кроме того, у электрона в атоме есть собственное магнитное поле, называемое спиновым.

Если при внесении во внешнее магнитное поле с индукцией В₀ внутри вещества создается индукция В < В₀, то такие вещества называются диамагнитными (n < 1).

В диамагнитных материалах при отсутствии внешнего магнитного поля магнитные поля электронов скомпенсированы, и при внесении их в магнитное поле индукция магнитного поля атома становится направленной против внешнего поля. Диамагнетик выталкивается из внешнего магнитного поля.

У парамагнитных материалов магнитная индукция электронов в атомах полностью не скомпенсирована, и атом в целом оказывается подобен маленькому постоянному магниту. Обычно в веществе все эти маленькие магниты ориентированы произвольно, и суммарная магнитная индукция всех их полей равна нулю. Если поместить парамагнетик во внешнее магнитное поле, то все маленькие магниты - атомы повернутся во внешнем магнитном поле подобно стрелкам компаса и магнитное поле в веществе усиливается (n >= 1).

Ферромагнитными называются такие материалы, в которых n " 1. В ферромагнитных материалах создаются так называемые домены, макроскопические области самопроизвольного намагничивания.

В разных доменах индукции магнитных полей имеют различные направления (рис. 61) и в большом кристалле

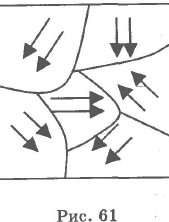
взаимно компенсируют друг друга. При внесении ферромагнитного образца во внешнее магнитное поле происходит смещение границ отдельных доменов так, что объем доменов, ориентированных по внешнему полю, увеличивается.

С увеличением индукции внешнего поля В₀ возрастает магнитная индукция намагниченного вещества. При некоторых значениях В₀ индукция прекращает резкий рост. Это явление называется магнитным насыщением.

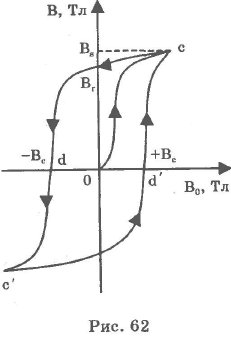
Характерная особенность ферромагнитных материалов - явление гистерезиса, которое заключается в неоднозначной зависимости индукции в материале от индукции внешнего магнитного поля при его изменении.

Петля магнитного гистерезиса - замкнутая кривая (cdc`d`c), выражающая зависимость индукции в материале от амплитуды индукции внешнего поля при периодическом достаточно медленном изменении последнего (рис. 62).

Петля гистерезиса характеризуется следующими величинами B_s, B_r, B_c. B_s - максимальное значение индукции материала при В_0s; В_r - остаточная индукция, равная значению индукции в материале при уменьшении индукции внешнего магнитного поля от B_0s до нуля; -В_с и В_с - коэрцитивная сила - величина, равная индукции внешнего магнитного поля, необходимого для изменения индукции в материале от остаточной до нуля.

Для каждого ферромагнетика существует такая температура (точка Кюри (Ж. Кюри, 1859-1906), выше которой ферромагнетик утрачивает свои ферромагнитные свойства.

Существует два способа приведения намагниченного ферромагнетика в размагниченное состояние: а) нагреть выше точки Кюри и охладить; б) намагничивать материал переменным магнитным полем с медленно убывающей амплитудой.

Ферромагнетики, обладающие малой остаточной индукцией и коэрцитивной силой, называются магнитомягкими. Они находят применение в устройствах, где ферромагнетику приходится часто перемагничиваться (сердечники трансформаторов, генераторов и др.).

Магнитожесткие ферромагнетики, обладающие большой коэрцитивной силой, применяются для изготовления постоянных магнитов.

Магнитное поле движущегося заряда

Любой проводник с током создает в окружающем пространстве магнитное поле. При этом электрический же ток является упорядоченным движением электрических зарядов. Значит можно считать, что любой движущийся в вакууме или среде заряд попрождает вокруг себя магнитное поле. В результате обобщения многочисленных опытных данных был установлен закон, который определяет поле В точечного заряда Q, движущегося с постоянной нерелятивистской скоростью v. Этот закон задается формулой   (1)  где r — радиус-вектор, который проведен от заряда Q к точке наблюдения М (рис. 1). Согласно (1), вектор В направлен перпендикулярно плоскости, в которой находятся векторы v и r : его направление совпадает с направлением поступательного движения правого винта при его вращении от v к r.  Рис.1 Модуль вектора магнитной индукции (1) находится по формуле   (2)  где α — угол между векторами v и r.  Сопоставляя закон Био-Савара-Лапласа и (1), мы видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока:    Приведенные законы (1) и (2) выполняются лишь при малых скоростях (v<<с) движущихся зарядов, когда электрическое поле движущегося с постоянной скорость заряда можно считать электростатическим, т. е. создаваемым неподвижным зарядом, который находится в той точке, где в данный момент времени находится движущийся заряд.  Формула (1) задает магнитную индукцию положительного заряда, движущегося со скоростью v. При движении отрицательнго заряда Q заменяется на -Q. Скорость v - относительная скорость, т. е. скорость относительно системы отсчета наблюдателя. Вектор В в данной системе отсчета зависит как от времени, так и от расположения наблюдателя. Поэтому следует отметить относительный характер магнитного поля движущегося заряда.  Первый, кто обнаружил поле движущегося заряда, был американский физик Г. Роуланду (1848—1901). Окончательно этот факт был установлен профессором Московского университета А. А. Эйхенвальдом (1863—1944), который изучал магнитное поле конвекционного тока и магнитное поле связанных зарядов поляризованного диэлектрика. Магнитное поле движущихся с постоянной скоростьб зарядов было измерено академиком А. Ф. Иоффе, который также доказал эквивалентность, в смысле возбуждения магнитного поля, электронного пучка и тока проводимости.

Вектор магнитной индукции — векторная физическая величина, направление которой в данной точке совпадает с направлением, указываемым в этой точке северным полюсом свободной магнитной стрелки.

2. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД

Сила Лоренца

- сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.

где q - заряд частицы; V - скорость заряда;  B - индукции магнитного поля; a - угол между вектором скорости заряда и вектором магнитной индукции.

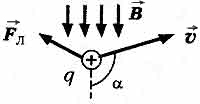
Направление силы Лоренца определяется по правилу левой руки:

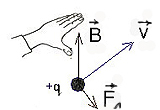
Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца . 

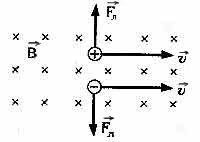
Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию). Если заряженная частица движется параллельно силовым линиям магнитного поля, то Fл = 0 , и заряд в магнитном поле движется равномерно и прямолинейно. Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной

  и создает центростремительное ускорение равное 

В этом случае частица движется по окружности.

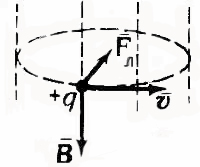.   Согласно второму закону Ньютона: сила Лоренца равнв произведению массы частицы на центростремительное ускорение 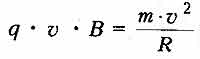   тогда радиус окружности 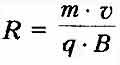   а период обращения заряда в магнитном поле

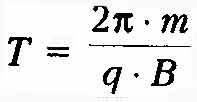
Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды.

МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА

Магнитные свойства вещества объясняются согласно гипотезе Ампера циркулирующими внутри любого вещества замкнутыми токами:

внутри атомов, вследствие движения электронов по орбитам, существуют элементарные электрические токи, которые создают элементарные магнитные поля. Поэтому: 1. если вещество не обладает магнитными свойствами - элементарные магнитные поля несориентированы ( из-за теплового движения);

2. если вещество обладает магнитными свойствами - элементарные магнитные поля одинаково направлены (сориентированы) и образуется собственное внутреннее магнитное поле вещества.

Намагничевание вещества - появление собственного внутреннего магнитного поля.

Все вещества, помещенные во внешнее магнитное поле, создают собственное внутреннее магнитное поле.

По своим магнитным свойствам все вещества подразделяются на: 

парамагнетики	диамагнетики	ферромагнетики
----------------------------------	-----------------------------------	-----------------------------
слабомагнитные вещества	слабомагнитные вещества	сильномагнитные вещества
O2, Al, Pb и др.	гелий, аргон, Au , Zn, Cu, вода, стекло и др.	неболшая группа кристаллич. тел: Fe, Ni, Co и сплавы
внутреннее магнитное поле направлено также, как и внешнее магнитное поле	внутреннее магнитное поле направлено противоположно внешнему магнитному полю, но слабовыражено	внутреннее магнитное поле в 100-1000 раз больше внешнего магнитного поля

Ферромагнетики сохраняют сильную намагниченность и после удаления внешнего магнитного поля и называютсяпостоянными магнитами. Сильное внутреннее магнитное поле ферромагнетиков объясняется не только обращением электронов по орбитам, но, в основном, вращением их вокруг собственной оси. Чтобы полностью размагнититьферромагнетик, надо поместить его во внешнее магнитное поле противоположно направленное. Существуют ферромагнетики, не проводящие электрический ток - ферриты.

Точка Кюри

Для каждого ферромагнетика существует определенная температура - точка Кюри.

1. Если t вещества < t Кюри, то вещество обладает ферромагнитными свойствами. 2. Если t вещества > t Кюри, то ферромагнитные свойства (намагниченность) исчезают, и вещество становится парамагнетиком.

Поэтому постоянные магниты при нагревании теряют свои магнитные свойства.

Магнитная проницаемость вещества

Если проводник с током создает в вакууме магнитное поле с магнитной индукцией Во, то в другой среде магнитное поле, созданное этим же проводником с током будет иметь индукцию В. Т.е. значение магнитной индукции зависит от среды, в которой существует магнитное поле. Отношение магнитной индукции В поля в данной среде к магнитной индукции Во в вакууме, характеризует магнитные свойства данной среды и называется относительной магнитной проницаемостью вещества - µ.

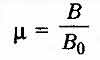
для диамагнетиков
для парамагнетиков
для ферромагнетиков

Применение ферромагнитов

- постоянные магниты, изготовление магнитной ленты и пленки; - сердечники трансформаторов, генераторов, электродвигателей.

3. Эффектом Холла называется возникновение разности потенциалов  (или поперечного электрического поля) в металле или полупроводнике, по которым проходит электрический ток I, при помещении их в магнитное поле, перпендикулярное к направлению тока. Пусть металлический проводник помещен в поле с индукцией  (как показано на рис. 4.12). Электроны проводимости под действием силы Лоренца  _л отклоняются к верхнему краю поверхности проводника и тогда у нижнего края возникает повышенная концентрация положительных зарядов. Между этими заряженными поверхностями возникает поперечное электрическое поле  _r. При определенной его величине устанавливается стационарное распределение зарядов, а разность потенциалов можно найти по формуле:

 = RJB/h, (4.24)

где R = 1/qn - постоянная Холла (q - заряд частицы, обуславливающий ток, n - концентрация носителей тока). При этом  , где j - вектор плотности тока. Эффект Холла позволяет определить концентрацию носителей тока, судить о характере проводимости (например, для полупроводников о дырочной, электронной или смешанной (n- и p- типа) проводимости).

  Рис.4.12.

Если имеется несколько проводников с различными токами, то суммарное магнитное поле, создаваемое системой токов, находится из принципа суперпозиции полей: магнитное поле  , создаваемое токами I₁, I₂, .. I_n , равно векторной сумме магнитных полей  ₁,  ₂, …  _n, создаваемых каждым током в отдельности.

Принцип суперпозиции магнитных полей позволяет найти индукцию магнитного поля   проводника конечной длины, по которому течет ток I, в любой точке поля:  . (4.3)

В частности, магнитные поля проводников с токами I различной конфигурации могут быть описаны соотношениями вида:

для прямолинейного проводника конечной длины (рис. 4.5,а)

B= _oJ(cos ₁ - cos ₂)/4 r_o (4.4)

для прямолинейного бесконечно длинного проводника (рис. 4.5,б)

B= _oJ/2 r_o (4.5)

в центре кругового проводника (рис. 4.5,в)

B= _oJ/2R (4.6)

на оси кругового витка с током (рис. 4.5,г)

B= _oJR²/[2(R² + r²)^3/2] (4.7)

в центре прямоугольного витка (рис. 4.5,д)

B=( _o/4 )8J(a² + b²)^1/2/ab (4.8)

   Рис. 4.5

Для проводников с током в виде замкнутого контура (например, в виде круга или прямоугольного витка) можно ввести вектор  , который называется магнитным моментом тока. Он по величине равен произведению тока I на площадь S , охватываемую контуром, и направлен по нормали n к плоскости контура так, чтобы из конца вектора   ток казался протекающим против часовой стрелки. Тогда формулы вида (4.6) и (4.7) могут быть записаны как:

B=( _o/2 )P_m/R³ ; B=( _o/2 )P_m/(R²+r²)^3/2 (4.9)

Таким образом, проводник с током создает в окружающем пространстве магнитное поле. Можно предположить, что и движущийся заряд порождает вокруг себя магнитное поле. Действительно, движущейся со скоростью   заряд q в однородной и изотропной среде порождает поле, магнитная индукция которого равна

 (4.10)

Здесь r - радиус-вектор, проведенный от заряде в рассматриваемую точку поля А (рис. 4.6)

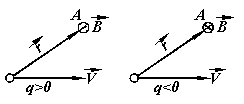  Рис.4.6.

Кружок с черточкой в центре означает, что вектор   направлен перпендикулярно плоскости рисунка к нам; кружок с крестиком в центре означает, что - вектор   направлен перпендикулярно плоскости рисунка от нас.

Магнитное поле движущегося заряда переменное, так как направление и величина   меняется при движении заряда (даже при   = const). Поскольку при движении заряда q вместе с ним перемещается электрическое поле напряженностью E = q /4 r³, то формулу (4.10) можно переписать в виде:   = _o[ _E ]. (4.11)

Формула (4.11) позволяет сделать вывод о том, что движущееся со скоростью  _E электрическое поле порождает магнитное поле.

Если в магнитное поле с индукцией   поместить проводник длиной dl с током I, то на проводник будет действовать сила d ₀, называемая силой Ампера, и которая определяется формулами:   (4.12)

В частности, если вектор   перпендикулярен вектору  , то направление силы Ампера можно найти по правилу левой руки: ладонь левой руки располагают так, чтобы вектор магнитной индукции  входил в ладонь, а четыре вытянутых пальца указывали направление тока, то отставленный большой палец левой руки укажет направление силы Ампера. Так как сила Ампера направлена перпендикулярно к линиям магнитной индукции, то она не является центральной (в отличие от электростатических сил, которые являются центральными).

4. Закон Био - Савара - Лапласа и его применение к расчету магнитного поля

Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791—1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.

Закон Био — Савара — Лапласа для проводника с током I, элемент dl  которого создает в некоторой точке А (рис. 164) индукцию поля dB, записывается в виде

                                                      (110.1)

где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r—радиус-вектор, проведанный из элемента dlпроводника в точку А поля, r — модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе.

Модуль вектора dB определяется выражением

                                                    (110.2)

где  — угол между векторами dl и r.

Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:

                                                      (110.3)

Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную сим­метрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.

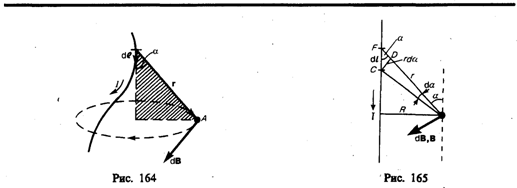
1. Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к вам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол  (угол между векторами dl и r), выразив через него все остальные величины. Из рис. 165 следует, что

(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна

                                                       (110.4)

Так как угол   для всех элементов прямого тока изменяется в пределах от 0 до , то, согласно (110.3) и (110.4),

Следовательно, магнитная индукция поля прямого тока

                                                                       (110.5)

5. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),

Тогда

Следовательно, магнитная индукция поля в центре кругового проводника с током

6. Основные формулы

      Сила, действующая на элемент   проводника с током  , помещенного в магнитное поле (сила Ампера),

 

,                                          (21)

где   – вектор магнитной индукции поля.

      Модуль силы Ампера, действующей на элемент проводника с током,

,                                          (22)

где   – угол между направлением векторов   и  .

      Полная сила, действующая на весь проводник с током, помещенный в магнитное поле с индукцией  ,

.                                          (23)

      Сила взаимодействия двух проводников с токами   и   (на единицу длины проводника)

,                                             (24)

где   – магнитная постоянная,   – расстояние между проводниками.

 

      Магнитный момент контура с током

,                                             (25)

где   – магнитный момент;   – сила тока;   – площадь, ограниченная контуром;   – вектор положительной нормали к контуру.

      Модуль магнитного момента

.                                                (26)

      Вращающий момент, действующий на контур с током, помещенный в магнитное поле,

,                                            (27)

где  – вращающий момент;   – магнитный момент;   – вектор магнитной индукции поля.

      Модуль вектора вращающего момента

,                                       (28)

где   – угол между векторами   и  .

      Сила, действующая на контур с током, помещенный в неоднородное магнитное поле (пондеромоторная сила),

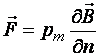,                                             (29)

где   – магнитный момент;   – градиент магнитной индукции поля.

 

      Модуль пондеромоторной силы

,                                      (30)

где   – угол между векторами   и  .

Пусть b – расстояние между двумя параллельными, бесконечно длинными проводниками (рис. 2.2). Задачу следует решать так: один из проводников    создаёт магнитное поле, второй    находится в этом поле.

            Магнитная индукция, создаваемая током    на расстоянии b от него:

,

(2.2.1)

      

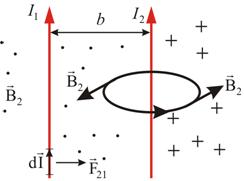
Рис. 2.2

      Если    и    лежат в одной плоскости, то угол между    и    прямой, следовательно   .  Тогда сила, действующая на элемент    тока   ,

,

(2.2.2)

      На каждую единицу длины проводника действует сила

,

(2.2.3)

(разумеется, со стороны первого проводника на второй действует точно такая же сила).

      Результирующая сила равна одной из этих сил. Если эти два проводника будут воздействовать на третий, тогда их магнитные поля    и Магнитное поле соленоида и тороида

Рассчитаем, применяя теорему о циркуля­ции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l,

188

имеющий N витков, по которому течет ток (рис. 175). Длину соленоида считаем во много раз больше, чем диаметр его витков, т. е. рассматриваемый соленоид бесконечно длинный. Экспериментальное изучение маг­нитного поля соленоида (см. рис. 162, б) показывает, что внутри соленоида поле является однородным, вне соленоида — неоднородным и очень слабым.

На рис. 175 представлены линии маг­нитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем меньше маг­нитная индукция вне его. Поэтому при­ближенно можно считать, что поле бес­конечно длинного соленоида сосредоточе­но целиком внутри него, а полем вне соленоида можно пренебречь.

Для нахождения магнитной индукции В выберем замкнутый прямоугольный кон­тур ABCDA, как показано на рис.175. Циркуляция вектора В по замкнутому кон­туру ABCDA, охватывающему все N вит­ков, согласно (118.1), равна

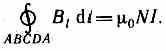
Интеграл по ABCDA можно представить в виде четырех интегралов: по АВ, ВС, CD и DA. На участках АВ и CD контур перпендикулярен линиям магнитной ин­дукции и В₁=0. На участке вне соленоида В=0. На участке DA циркуляция векто­ра В равна Вl (контур совпадает с линией магнитной индукции); следовательно,

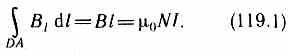
да (в вакууме):

B=₀NI/l. (119.2)

Получили, что поле внутри соленоида од­нородно (краевыми эффектами в об­ластях, прилегающих к торцам соленоида, при расчетах пренебрегают). Однако от­метим, что вывод этой формулы не совсем корректен (линии магнитной индукции за­мкнуты, и интеграл по внешнему участку магнитного поля строго нулю не равен). Корректно рассчитать поле внутри солено­ида можно применяя закон Био — Сава­ра — Лапласа; в результате получается та же формула (119.2).

• нужно сложить векторно.

7. Магнитное поле соленоида и тороида

Рассчитаем, применяя теорему о циркуля­ции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l,

188

имеющий N витков, по которому течет ток (рис. 175). Длину соленоида считаем во много раз больше, чем диаметр его витков, т. е. рассматриваемый соленоид бесконечно длинный. Экспериментальное изучение маг­нитного поля соленоида (см. рис. 162, б) показывает, что внутри соленоида поле является однородным, вне соленоида — неоднородным и очень слабым.

На рис. 175 представлены линии маг­нитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем меньше маг­нитная индукция вне его. Поэтому при­ближенно можно считать, что поле бес­конечно длинного соленоида сосредоточе­но целиком внутри него, а полем вне соленоида можно пренебречь.

Для нахождения магнитной индукции В выберем замкнутый прямоугольный кон­тур ABCDA, как показано на рис.175. Циркуляция вектора В по замкнутому кон­туру ABCDA, охватывающему все N вит­ков, согласно (118.1), равна

Интеграл по ABCDA можно представить в виде четырех интегралов: по АВ, ВС, CD и DA. На участках АВ и CD контур перпендикулярен линиям магнитной ин­дукции и В₁=0. На участке вне соленоида В=0. На участке DA циркуляция векто­ра В равна Вl (контур совпадает с линией магнитной индукции); следовательно,

да (в вакууме):

B=₀NI/l. (119.2)

Получили, что поле внутри соленоида од­нородно (краевыми эффектами в об­ластях, прилегающих к торцам соленоида, при расчетах пренебрегают). Однако от­метим, что вывод этой формулы не совсем корректен (линии магнитной индукции за­мкнуты, и интеграл по внешнему участку магнитного поля строго нулю не равен). Корректно рассчитать поле внутри солено­ида можно применяя закон Био — Сава­ра — Лапласа; в результате получается та же формула (119.2).

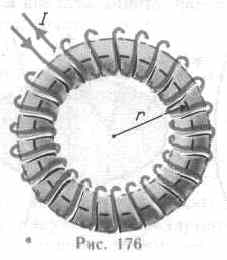
8. Важное значение для практики имеет также магнитное поле тороида—кольце­вой катушки, витки которой намотаны на сердечник, имеющий форму тора (рис. 176). Магнитное поле, как показыва­ет опыт, сосредоточено внутри тороида, вне его поле отсутствует.

Линии магнитной индукции в данном случае, как следует из соображений сим­метрии, есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиуса r. Тогда, по теореме о циркуля­ции (118.1),

B•2r=₀NI,

откуда следует, что магнитная индукция внутри тороида (в вакууме)

В=₀NI/(2r),

где N — число витков тороида.

Если контур проходит вне тороида, то токов он не охватывает и В•2r=0. Это означает, что поле вне тороида отсутству­ет (что показывает и опыт).

9. На проводник с током в магнитном поле действуют силы, которые определяются с помощью закона Ампера. Если проводник не закреплен (например, одна из сторон контура сделана в виде подвижной перемычки, рис. 1), то под действием силы Ампера он в магнитном поле будет перемещаться. Значит, магнитное поле совершает работу по перемещению проводника с током.  Для вычисления этой работы рассмотрим проводник длиной l с током I (он может свободно двигаться), который помещен в однородное внешнее магнитное поле, которое перпендикулярно плоскости контура. Сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера, рассчитывается по формуле    Под действием данной силы проводник передвинется параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, которая совершается магнитным полем, равна    так как ldx=dS — площадь, которую пересекает проводник при его перемещении в магнитном поле, BdS=dФ — поток вектора магнитной индукции, который пронизывает эту площадь. Значит,   (1)  т. е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником. Данная формула справедлива и для произвольного направления вектора В.  Рассчитаем работу по перемещению замкнутого контура с постоянным током I в магнитном поле. Будем считать, что контур М перемещается в плоскости чертежа и в результате бесконечно малого перемещения перейдет в положение М', изображенное на рис. 2 штриховой линией. Направление тока в контуре (по часовой стрелке) и магнитного поля (перпендикулярно плоскости чертежа — за чертеж или от нас) дано на рисунке. Контур М условно разобьем на два соединенных своими концами проводника: AВС и CDА.  Работа dA, которая совершается силами Ампера при иссследуемом перемещении контура в магнитном поле, равна алгебраической сумме работ по перемещению проводников AВС (dA₁) и CDA (dA₂), т. е.   (2)  Силы, которые приложенны к участку CDA контура, образуют острые углы с направлением перемещения, поэтому совершаемая ими работа dA₂>0. .Используя (1), находим, эта работа равна произведению силы тока I в нашем контуре на пересеченный проводником CDA магнитный поток. Проводник CDA пересекает при своем движении поток dФ₀ сквозь поверхность, выполненную в цвете, и поток dФ₂, который пронизывает контур в его конечном положении. Значит,   (3)  Силы, которые действуют на участок AВС контура, образуют тупые углы с направлением перемещения, значит совершаемая ими работа dA₁<0. Проводник AВС пересекает при своем движении поток dФ₀ сквозь поверхность, выполненную в цвете, и поток dФ1, который пронизывает контур в начальном положении. Значит,   (4)  Подставляя (3) и (4) в (2), найдем выражение для элементарной работы:    где dФ₂—dФ₁=dФ' — изменение магнитного потока сквозь площадь, которая ограничена контуром с током. Таким образом,   (5)  Проинтегрировав выражение (5), найдем работу, которая совершается силами Ампера, при конечном произвольном перемещении контура в магнитном поле:   (6)  значит, работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром. Выражение (6) верно для контура любой формы в произвольном магнитном поле. 

10. Явление электромагнитной индукции было открыто Майклом Фарадеем в 1831 г. Он опытным путем установил, что при изменении магнитного поля внутри замкнутого контура в нем возникает электрический ток, который называют индукционным током. Опыты Фарадея можно воспроизвести следующим образом: при внесении или вынесении магнита в катушку, замкнутую на гальванометр, в катушке возникает индукционный ток (рис. 34). Если рядом расположить две катушки (например, на общем сердечнике или одну катушку внутри другой) и одну катушку через ключ соединить с источником тока, то при замыкании или размыкании ключа в цепи первой катушки во второй катушке появится индукционный ток (рис. 35). Объяснение этого явления было дано Максвеллом. Любое переменное магнитное поле всегда порождает переменное электрическое поле.  Для количественной характеристики процесса изменения магнитного поля через замкнутый контур вводится физическая величина под названием «магнитный поток». Магнитным потоком через замкнутый контур площадью S называют физическую величину, равную произведению модуля вектора магнитной индукции Б на площадь контура S и на косинус угла а между направлением вектора магнитной индукции и нормалью к площади контура. Ф = BS cos а (рис. 36).         Опытным путем был установлен основной закон электромагнитной индукции: ЭДС индукции в замкнутом контуре равна по величине скорости изменения магнитного потока через контур. . Если рассматривать катушку, содержащую п витков, то формула основного закона электромагнитной индукции будет выглядеть так: .  Единица магнитного потока Ф — вебер (Вб): 1В6 = = 1В-с.  Из основного закона следует смысл размерности: 1 вебер — это величина такого магнитного потока, который, уменьшаясь до нуля за одну секунду, через замкнутый контур наводит в нем ЭДС индукции 1 В.  Классической демонстрацией основного закона электромагнитной индукции является первый опыт Фарадея: чем быстрее перемещать магнит через витки катушки, тем больше возникает индукционный ток в ней, а значит, и ЭДС индукции.  Зависимость направления индукционного тока от характера изменения магнитного поля через замкнутый контур в 1833 г. опытным путем установил русский ученый Ленц. Он сформулировал правило, носящее его имя. «Индукционный ток имеет такое направление, при котором его магнитное поле стремится скомпенсировать изменение внешнего магнитного потока через контур». Ленцем был сконструирован прибор, представляющий собой два алюминиевых кольца, сплошное и разрезанное, укрепленные на алюминиевой перекладине и имеющие возможность вращаться вокруг оси, как коромысло (рис. 37). При внесении магнита в сплошное кольцо оно начинало "убегать" от магнита, поворачивая соответственно коромысло. При вынесении магнита из кольца кольцо стремилось «догнать» магнит. При движении магнита внутри разрезанного кольца никакого эффекта не происходило. Ленц объяснял опыт тем, что магнитное поле индукционного тока стремилось компенсировать изменение внешнего магнитного потока.