Шифрование

Сообщение   шифруется следующим образом:

1. Выбирается сессионный ключ — случайное целое число   такое, что 

2. Вычисляются числа   и  .

3. Пара чисел   является шифротекстом.

Нетрудно видеть, что длина шифротекста в схеме Эль-Гамаля длиннее исходного сообщения   вдвое.

Расшифрование:

Зная закрытый ключ  , исходное сообщение можно вычислить из шифротекста   по формуле:

При этом нетрудно проверить, что

и поэтому

.

Для практических вычислений больше подходит следующая формула:

Так как в схему Эль-Гамаля вводится случайная величина  ,то шифр Эль-Гамаля можно назвать шифром многозначной замены. Из-за случайности выбора числа   такую схему еще называют схемой вероятностного шифрования. Вероятностный характер шифрования является преимуществом для схемы Эль-Гамаля, так как у схем вероятностного шифрования наблюдается большая стойкость по сравнению со схемами с определенным процессом шифрования. Недостатком схемы шифрования Эль-Гамаля является удвоение длины зашифрованного текста по сравнению с начальным текстом. Для схемы вероятностного шифрования само сообщение   и ключ не определяют шифротекст однозначно. В схеме Эль-Гамаля необходимо использовать различные значения случайной величины   для шифровки различных сообщений   и  . Если использовать одинаковые  , то для соответствующих шифротектов   и   выполняется соотношение  . Из этого выражения можно легко вычислить  , если известно  .

Цифровая подпись служит для того чтобы можно было установить изменения данных и чтобы установить подлинность подписавшейся стороны. Получатель подписанного сообщения может использовать цифровую подпись для доказательства третьей стороне того, что подпись действительно сделана отправляющей стороной. При работе в режиме подписи предполагается наличие фиксированной хеш-функции  , значения которой лежат в интервале  .

Подпись сообщений

Для подписи сообщения   выполняются следующие операции:

1. Вычисляется дайджест сообщения  : 

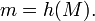
2. Выбирается случайное число   взаимно простое с 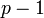  и вычисляется 

3. Вычисляется число  .

4. Подписью сообщения   является пара  .

Проверка подписи

Зная открытый ключ  , подпись   сообщения   проверяется следующим образом:

1. Проверяется выполнимость условий:   и  . Если хотя бы одно из них не выполняется, то подпись считается неверной.

2. Вычисляется дайджест 

3. Подпись считается верной, если выполняется сравнение: