8) Матрицы. Осн.Понятия.И опр.

Прямоугольная таблица чисел вида

A=

Называется матрицей . Здесь (i=1,2,.., m, j=1,2,…, n)называемые элементами матрицы, i и j индексы строки и столбца. При этом произведение m*n числа строк на число столбцов называют размером матрицы А.

Матр все эл-ты кот =0, назыв нулевой матрицей.

Когда m=n матр назыв квадратной.

Упорядоченная совокупность элементов называется главной диагональю квадратной матрицы.

Квадр матр назыв диагональной,если ее эл-ты удовл усл

Ненулевыми могут быть только элементы главной диагонали.

Единичной матр назыв диагональная матрица, у кот все элементы гл диаг =1.

Две матрицы назыв равными (А=В),если они имеют одинаковые размеры и их соответствующие элементы равны.

9) Операции над матрицами

1)Суммой матриц АиВ одинакового размера назыв матрица С того же размера, каждый элемент кот равен сумме соответствующих элем-ов матриц АиВ.

А= i=1,2…m

B= j=1,2…n

C=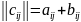

2)Произведением матрицы А на действ число  называется матрица, кажд эл-нт кот получен умножением соотв элемента матрицы А на число .

Свойства матриц:

1. A+B=B+A (коммутативный закон сложения)

2. A+(B+C)=(A+B)+C (ассоциативный закон)

3. α∙(A+B) =α∙A+ α∙B(дистрибутивный закон)

4. (α+β)∙A= α∙A+ β∙A

5. α∙( βA)= (α β)∙A

6. A+0=A ( закон поглощения нуля)

7. А0=0

3)Транспонированием матрицы называется замена строк матрицы на ее столбцы с сохранением их порядка.

- дважды транспонир матрица равна исходной

- при транспонир квадратных матриц элементы,находящ. на главной диагонали, не меняют своих позиций.

- транспонирование симметрических матриц А=А’

4)Произведением матриц А и В назыв матр С, элем кот

С=АВ=

=

j=1,2….n

Произведение матриц А и В имеет смысл, если число столбцов А равно числу строк В.

Св-ва

1)(АВ)С=А(ВС)

2)(А+В)С=АС+ВС

3)А(В+С)=АВ+АС

4)(АВ)=(А)В

5)Е-единичн матр играет роль единицы АЕ=А

10)Определитель матрицы. Свойства определителя

Любой квадратной матрице А порядка n ставится в соответствие по определенному закону некоторое число, называемое определителем или детерминантом n-ого порядка этой матрицы.

А=

Опр-ль второго порядка:

2= =

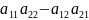
Из произведения элементов на главной диаг вычитается произвед элементов на второй диаг.

Опр-ль третьего порядка

3= =

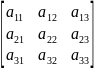Определителем матрицы А n-ого порядка называется алгебраическая сумма n! произведений n-ого порядка элементов этой матрицы, причем каждое произведение входит по одному эл-ту из каждой строки и каждого столбца данной матрицы.

Важнейшей числовой характеристикой квадратной матрицы является определитель, который для матрицы An,n обозначается следующим образом: |A| или det (A). Размерность матрицы, для которой ищется определитель, задает его порядок.

Если квадратная матрица имеет определитель, отличный от нуля (Δ ≠ 0), то говорят, что матрица невырожденная, в противном случае - матрица вырожденная или особая.

Свойства определителя:

1. Общий множитель любой строки (столбца) можно выносить за знак определителя.

2. Если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, то величина определителя не изменится.

3. Если в определителе есть нулевая строка (столбец), то определитель равен нулю.

4. При перестановке двух строк (столбцов) определитель меняет знак на противоположный.

5. Определитель с двумя одинаковыми строками (столбцами) равен нулю.

6. При транспонировании матрицы ее определитель не меняется.

7.При умножении какой-либо строки (столбца) матрицы на произвольное число, сам определитель матрицы увеличивается в это же число раз.