Вопрос 13 « Характерные точки и участки диаграммы растяжения. Предельные и допускаемые напряжения.»

диаграммой растяжения.

На рис. 3.3 изображен типичный вид диаграммы для ма­лоуглеродистой стали, как примера наиболее распространен­ного пластичного конструкционного материала. Рассмотрим характерные участки и точки этой диаграммы:

OA - прямая, справедлив закон Гука;

AB - закон Гука нарушается, но при снятии нагрузки об­разец полностью восстанавливает свои первоначальные раз­меры, отсутствует остаточная деформация;

CD - площадка текучести, удлинение образца происхо­дит при постоянной нагрузке;

DM - зона упрочнения, требуется увеличение нагрузки для дальнейшего растяжения образца;

M - точка, соответствующая наибольшей силе, достиг­нутой при испытании. До точки M деформации распределены по длине образца равномерно, поэтому участок BM иногда называют зоной равномерных упругопластических дефор­маций;

MK - зона местных деформаций, на образце появляется сужение («шейка»), в которой и происходит основной рост деформаций;

K - точка диаграммы, соответствующая моменту разры­ва образца.

Если с некоторой произвольной точки диаграммы Е на­чать разгружать образец, то этот процесс опишется прямой ЕЕ', практически параллельной начальному участку ОА.

Отрезок ОЕ" равен полному удлинению в точке Е и склады­вается из остаточной (отрезок ОЕ') и упругой (отрезок Е'Е") частей.

Если теперь начать вновь растягивать образец, то диа­грамма пойдёт примерно по прямой EE , а затем вдоль линии EMK так, как будто разгрузки и повторной нагрузки не было. Иными словами, при нагружении образца выше предела текучести и последующей разгрузке металл меняет свои свойства - исчезает площадка текучести, повышается предел пропорциональности, уменьшается относительное удлинение при разрыве - материал становится более хрупким. Это явление называется наклёпом, оно возникает не только при растяжении, но и при других видах нагружения. Иногда наклёп вызывается специально, иногда он является нежела­тельным следствием предшествующих методов механиче­ской обработки. В этих случаях с ним приходится бороться, в частности, с помощью отжига изделия.

Существуют три основных метода расчета элементов

конструкций на прочность:

– метод допускаемых напряжений;

– метод предельных состояний;

– метод разрушающих нагрузок.

Метод допускаемых напряжений

Этот метод является основным при расчете машиностроительных конструкций. В его основе лежит условие

Прочности σmax ≤ [σ],

которое для случая растяжения (сжатия) приобретает вид

σmax =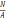 ≤ [σ]

где σmax – наибольшее по величине напряжение, возникающее в опасных точках наиболее нагруженного сечения;

[σ] – допускаемое напряжение, которое для каждого материала находится по формуле

Здесь σоп – опасное напряжение, за которое принимают либо предел текучести при статическом нагружении для пластичных материалов, либо предел прочности для хрупких;

n – коэффициент запаса прочности, учитывающий весь комплекс факторов, влияющих на точность расчетов – разброс механических характеристик материала, погрешности методик расчета, упрощение условий нагружения, особенности работы конструкции и т. д. Коэффициенты запаса назначаются техническими условиями и нормами проектирования, они могут существенно различаться в разных отраслях производства. Для пластичных материалов коэффициент запаса принимается обычно равным n = 1.4…1.6, для хрупких n = 2.5…3.5. С развитием техники, ростом качества производства и точности расчетов коэффициенты запаса имеют тенденцию к понижению.

Метод предельных состояний

Этот метод используется в настоящее время при строительстве промышленных и гражданских зданий и сооружений. Он позволяет учесть большинство факторов, от которых зависит прочность сооружения или его отдельных элементов – особенности нагрузок и других воздействий, свойства материала, геометрию конструкции, условия работы, степень ответственности сооружения и т. д.

Условие прочности элементов, работающих на растяжение (сжатие) имеет вид

σmax = ≤ R

Здесь R – расчетное сопротивление материала – напряжение, при котором конструкция может перейти в предельное состояние;

R = ,

где Rн – нормативное сопротивление материала, принимаемое обычно равным соответствующей характеристике прочности – пределу текучести для пластичных и пределу прочности для хрупких материалов;

γм – коэффициент надёжности по материалу, учитывающий возможность статистического отклонения характеристик материала от справочных значений. Этот коэффициент устанавливается Строительными нормами и правилами (СНиП) и составляет для металлов величину 1.025…1.15, для бетона1.3…1.5.

Особенности нестатистического характера, такие как агрессивность среды, температурный режим, непостоянство нагрузок и т. п. учитывают умножением расчетного сопротивления на коэффициент условий работы γ, который также устанавливается СНиПом; в большинстве случаев при нормальных условиях работы он равен единице и может быть 50 опущен. В ряде случаев расчетное сопротивление может со держать и другие коэффициенты, в частности коэффициент надежности по назначению γн, учитывающий значимость последствий наступления предельного состояния.

Входящая в условие прочности (3.2) величина N – расчетное усилие – определяется следующим образом:

N= N_нn ,

где Nн – нормативное усилие, возникающее в элементах конструкции от действия нормативных нагрузок, устанавливаемых строительными нормами;

n – коэффициент надежности по нагрузке, учитывающий отклонение нагрузок от нормативных в процессе строительства и эксплуатации сооружения.