9 Теорема о движении центра масс.
Теорема Центр масс системы движется так же, как и материальная точка, масса которой равна массе всей системы, если на точку действуют все внешние силы, приложенные к рассматриваемой механической системе.
,
следовательно
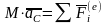
Дифференциальные уравнения движения системы.
Рассмотрим
систему, состоящую из п
материальных точек. Выделим какую-нибудь
точку системы с массой
.
Обозначим равнодействующую всех
приложенных к точке внешних сил (и
активных и реакций связей) через
,
а равнодействующую всех внутренних сил
- через
.
Если точка имеет при этом ускорение
,
то по основному закону динамики
.
Аналогичный результат получим для любой точки. Следовательно, для всей системы будет:
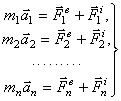
Эти
уравнения, из которых можно определить
закон движения каждой точки системы,
называются дифференциальными
уравнениями движения системы
в векторной форме. Уравнения являются
дифференциальными, так как
;
входящие в правые части уравнений силы
будут в общем случае зависеть от времени,
координат точек системы и их скоростей.
Закон сохранения движения центра масс.
Из теоремы о движении центра масс можно получить следующие важные следствия:
1) Пусть сумма внешних сил, действующих на систему, равна нулю
Тогда
из уравнения
следует,
что
или
Следовательно, если
сумма всех внешних сил, действующих на
систему, равна нулю, то центр масс этой
системы движется с постоянной по модулю
и направлению скоростью, т. е. равномерно
и прямолинейно.
В частности, если вначале центр масс
был в покое, то он и останется в покое.
Действие внутренних сил, как мы видим,
движение центра масс системы изменить
не может.
2) Пусть сумма внешних сил, действующих на систему, не равна нулю, но эти силы таковы, что сумма их проекций на какую-нибудь ось (например, ось Ох) равна нулю:
Тогда
уравнение
дает:
или
Следовательно, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция скорости центра масс системы на эту ось есть величина постоянная.
10 Теорема об изменении количества движения системы.
Количеством движения системы материальных точек называется векторная сумма количеств движений отдельных точек системы.
Эта теорема существует в трех различных формах.
Теорема. Производная по времени от количества движения системы равна векторной сумме всех внешних сил, действующих на систему.
, (6.1)
Доказательство: Теорема об изменении количества движения для точки имеет вид:
,
Сложим все уравнений и получим:
,
что и требовалось доказать.
В проекциях на оси координат это утверждение выглядит так:
, , .
Теорема. (в дифференциальной форме). Дифференциал от количества движения системы равен сумме элементарных импульсов всех внешних сил, действующих на систему.
Умножим левую и правую части уравнения (6.1) на и получим
, (6.2)
В проекциях на оси координат это утверждение выглядит так:
, , .
Теорема (в интегральной форме). Изменение количества движения системы за какой-либо промежуток времени равно векторной сумме элементарных импульсов всех внешних сил, действующих на систему за этот же промежуток времени.
Интегрируя обе части уравнения (**) по времени в пределах от нуля до получаем:
В проекциях на оси координат это утверждение выглядит так:
, , .