
- •2 Динамика точки
- •4 Две основные задачи динамики материальной точки
- •5 Относительное движение материальной точки
- •Введение в динамику механической системы
- •7 Моменты инерции
- •8 Общие теоремы динамики системы и твердого тела Количество движения системы.
- •Теорема об изменении количества движения системы.
- •9 Теорема о движении центра масс.
- •10 Теорема об изменении количества движения системы.
- •Элементарный и полный импульс силы.
- •13 Главный Момент количества движения системы.
- •Кинетический Момент количества движения твердого тела относительно оси вращения при вращательном движении твердого тела.
- •Теорема об изменении кинетического момента количества движения системы.
- •Законы сохранения кинетического момента количества движения.
- •14 Работа силы. Мощность.
- •15 Кинетическая энергия механической системы.
- •Теорема об изменении кинетической энергии системы.
- •16 Динамика твердого тела
- •17 Принцип Даламбера для материальной точки
- •20 Уравнения Лагранжа 2-го рода:
2 Динамика точки
Материальной точкой называют материальное тело (тело, имеющее массу), размерами которого при изучении его движения можно пренебречь.
Практически данное тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела при его движении, очень велики по сравнению с размерами самого тела. Кроме того, как будет показано в динамике системы поступательно движущееся тело можно всегда рассматривать как материальную точку с массой, равной массе всего тела.
Наконец, материальными точками можно считать частицы, на которые мы будем мысленно разбивать любое тело при определении тех или иных его динамических характеристик.
Точку будем называть изолированной, если на точку не оказывается никакого влияния, никакого действия со стороны других тел и среды, в которой точка движется. Конечно, трудно привести пример подобного состояния. Но представить такое можно.
4 Две основные задачи динамики материальной точки
Первая или прямая задача:
Известна масса точки и закон ее движения, необходимо найти действующую на точку силу.
m
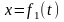
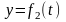
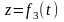
Вычисляем вторые производные по времени от координат точки, умножаем их на массу и получаем проекции силы на оси координат
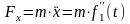
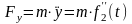
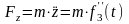
Зная проекции силы на оси координат, определяем модуль силы и ее направляющие косинусы:
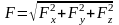
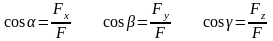
Пример 1: Движение точки в плоскости xOy определяется уравнениями:
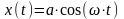 ;
; 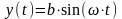 ;
; 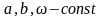 ;
; 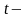 время.
время.
Решение:
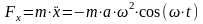 ;
;
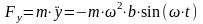
 ;
;
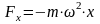 ;
;
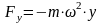 .
.
 -
Уравнение траектории в координатной
форме (эллипс).
-
Уравнение траектории в координатной
форме (эллипс).
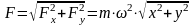
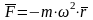 ;
; 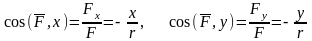
5 Относительное движение материальной точки
Во многих задачах динамики движение материальной точки рассматривается относительно системы отсчета, движущейся относительно инерциальной системы отсчета.
П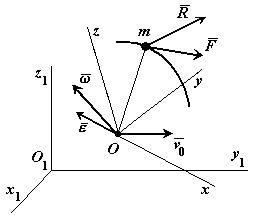 олучим
дифференциальные уравнения движения
материальной точки относительно
подвижной системы отсчета.
олучим
дифференциальные уравнения движения
материальной точки относительно
подвижной системы отсчета.
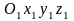 -
инерциальная система отсчета.
-
инерциальная система отсчета.
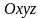 -
подвижная система отсчета.
-
подвижная система отсчета.
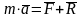 ,
,
где
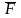 - сумма активных сил,
- сумма активных сил,
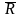 - сумма сил реакции связи.
- сумма сил реакции связи.
Согласно
теореме Кориолиса
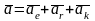
Перепишем дифференциальное уравнение следующим образом
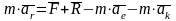
Введем обозначения
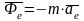 -
переносная сила инерции,
-
переносная сила инерции,
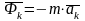 -
кориолисова сила инерции.
-
кориолисова сила инерции.
С учетом этих обозначений мы получаем динамическую теорему Кориолиса (уравнения относительного движения).
Материальная точка движется относительно неинерциальной системы отсчета так же как и относительно инерциальной, только к приложенным активным силам и силам реакции связей следует добавить кориолисову и переносную силу инерции.
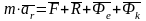
Силы
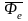 и
и
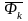 являются поправками на неинерционность
системы.
являются поправками на неинерционность
системы.
В проекциях на подвижные оси
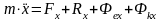
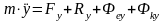
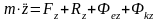
Введение в динамику механической системы
Механической системой называется любая система материальных точек и тел.
Внешними силами механической системы называются силы, с которыми на точки и тела механической системы действуют точки и тела не входящие в рассматриваемую систему.
Равнодействующая
всех внешних сил приложенных к
 точке
обозначается
точке
обозначается
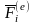 (от латинского exterior
- внешний).
(от латинского exterior
- внешний).
Внутренними силами механической системы называются силы взаимодействия между точками и телами рассматриваемой системы.
Равнодействующая
всех внутренних сил приложенных к
точке
обозначается
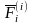 (от латинского interior
- внутренний).
(от латинского interior
- внутренний).
Это разделение является условным и зависит от того, какая механическая система рассматривается.
Внутренние силы системы обладают следующими свойствами:
Теорема.
Главный вектор всех внутренних сил
системы (векторная сумма) равен нулю
при любом состоянии системы.
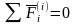 .
.
Доказательство: Согласно одной из аксиом динамики, любые две точки системы действуют друг на друга с равными по величине, но противоположно направленными силами. Векторная сумма этих сил равна нулю. Все внутренние силы являются большим количеством таких парных сил. Поэтому сумма всех внутренних сил равна нулю.
Теорема.
Главный момент всех внутренних сил
системы (векторная сумма) относительно
любой точки или оси равен нулю при любом
состоянии системы.
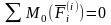 или
или
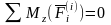 .
.
Доказательство: Любые две точки системы действуют друг на друга с равными по величине, но противоположно направленными силами. Сумма моментов этих сил относительно любой точки или оси равна нулю. Все внутренние силы являются большим количеством таких парных сил. Поэтому сумма моментов всех внутренних сил относительно любой точки или оси равна нулю.
Дифференциальные уравнения системы в векторной форме:
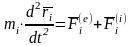 ,
,
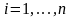
Ц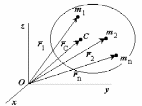 ентром
масс механической
системы называется геометрическая
точка С, радиус-вектор которой
ентром
масс механической
системы называется геометрическая
точка С, радиус-вектор которой
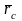 определяется выражением
определяется выражением
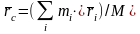
где 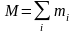 - масса системы.
- масса системы.
