
- •Кинематика движения материальной точки Радиус-вектор, траектория перемещение, путь скорости, ускорение Нормальное тангенциальное полное ускорение
- •2. Кинематика движения по окружности Угловые характеристики движения Связь между линейными и угловыми характеристиками
- •3. Динамика поступательного движения материальной точки Законы Ньютона Инерциальные системы отсчета Принцип относительности Галилея преобразования Галилея
- •4 . Импульс Закон сохранения импульса.
- •5. Динамика твердого тела поступательное и вращательное движение Понятие момента силы и момента импульса относительно точки и неподвижной оси
- •6.Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси
- •7. Понятие момента инерции твердого тела Пример расчета Теорема Штейнера
- •Свободные затухающие колебания Дифференциальное уравнение, его решение Характеристики затухания.
- •Релятивистский импульс
Свободные затухающие колебания Дифференциальное уравнение, его решение Характеристики затухания.
Затуханиемколебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой.
Получим дифференциальное уравнение свободных затухающих колебаний на примере реального пружинного маятника, совершающего колебания в среде с сопротивлением (простейший случай - трение о воздух). Пусть масса маятника m, коэффициент упругости пружины k, сила сопротивления, действующая на маятник, F = - bv, v - скорость маятника, b - коэффициент сопротивления среды, в которой находится маятник. Так как мы рассматриваем только линейные системы, b = const, k = const. x - смещение маятника от положения равновесия.
Второй закон Ньютона в нашем случае запишется так:
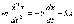
Это уравнение и есть дифференциальное уравнение свободных затухающих колебаний пружинного маятника. Его, однако, принято записывать в следующем, так называемом каноническом виде:
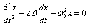
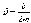 -
коэффициент затухания,
-
коэффициент затухания,
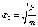 - собственная частота свободных
(незатухающих) колебаний пружинного
маятника, то, что раньше мы обозначали
просто .
- собственная частота свободных
(незатухающих) колебаний пружинного
маятника, то, что раньше мы обозначали
просто .
Уравнение затухающих колебаний в таком (каноническом) виде описывает затухающие колебания всех линейных систем; конкретная колебательная система отличается только выражениями для и .

16. Вынужденные механические колебания. Дифференциальное уравнение его решение Явление резонанса. Резонансная частота
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам),
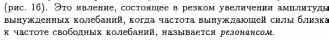
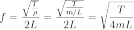
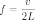
T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.
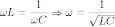
где
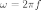 ;
f — резонансная частота в герцах; L —
индуктивность в генри;
C — ёмкость в фарадах.
;
f — резонансная частота в герцах; L —
индуктивность в генри;
C — ёмкость в фарадах.
Дифференциальное уравнение вынужденных колебаний и его решение
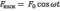
Где
 – максимальное значение вынужденной
силы,
– максимальное значение вынужденной
силы,
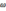 – циклическая частота колебаний
вынуждающей силы.
– циклическая частота колебаний
вынуждающей силы.
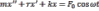 – дифференциальное
уравнение вынужденных колебаний.
– дифференциальное
уравнение вынужденных колебаний.
Это уравнение делим на m
Обозначим
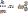 ;
;
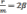 ;
;
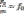 .
.
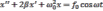
Если
внешняя сила не действует, т.е.
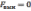 ,
то
,
то
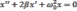 –
уравнение свободных колебаний.
–
уравнение свободных колебаний.
r – коэффициент сопротивления среды.
 -
сила сопротивления
-
сила сопротивления
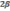 -
коэффициент характеристики сопротивления
среды
-
коэффициент характеристики сопротивления
среды
Если
сопротивление отсутствует, т.е.
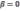 ,
то
,
то
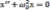 - уравнение собственных колебаний
системы.
- уравнение собственных колебаний
системы.
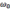 -
частота собственных колебаний системы.
-
частота собственных колебаний системы.
17. Принцип относительности в классической и релятивистской механике Постулаты СТО (Эйнштейна) Преобразования Лоренца
Классическая механика
Во всех инерциальных системах отсчета механические явления протекают одинаково (при одинаковых начальных условиях)
Релятивистская механика
Во всех инерциальных системах отсчета механические явления протекают одинаково (при одинаковых начальных условиях)
Постулаты СТО(Специальная теория относительности)
Принцип относительности: все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. Это означает, что во всех инерциальных системах физические законы (не только механические) имеют одинаковую форму. Таким образом, принцип относительности классической механики обобщается на все процессы природы, в том числе и на электромагнитные. Этот обобщенный принцип называют принципом относительности Эйнштейна.
Принцип постоянства скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Скорость света в СТО занимает особое положение. Это предельная скорость передачи взаимодействий и сигналов из одной точки пространства в другую.
Преобразования Лоренца − преобразования координат и времени какого-либо события при переходе от одной инерциальной системы отсчёта к другой.
18. Следствия из преобразований Лоренца, сокращение длины замедление времени, одновременность событии.
О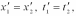 тносительность
одновременности.Пусть
в системе К
в точках с координатами x1
и x2
в моменты времени t1
и t2
происходят два события. В системе К'
им соответствуют координаты x'1
и x'2
и моменты времени t'1
и t'2.
Если события в системе К
происходят в одной точке (x1
= x2)
и являются одновременными (t1
= t2),
то, согласно преобразованиям Лоренца,
тносительность
одновременности.Пусть
в системе К
в точках с координатами x1
и x2
в моменты времени t1
и t2
происходят два события. В системе К'
им соответствуют координаты x'1
и x'2
и моменты времени t'1
и t'2.
Если события в системе К
происходят в одной точке (x1
= x2)
и являются одновременными (t1
= t2),
то, согласно преобразованиям Лоренца,
т.е.
эти события являются одновременными и
пространственно совпадающими для любой
инерциальной системы отсчета.
Если
события в системе К
пространственно разобщены (x1
≠ x2),
но одновременны (t1
= t2),
то в системе К',
согласно преобразованиям Лоренца. 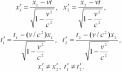 Таким
образом, в системе К'
эти события, оставаясь
пространственно разобщенными, оказываются
и неодновременными.
Таким
образом, в системе К'
эти события, оставаясь
пространственно разобщенными, оказываются
и неодновременными.
2. Длительность событий в разных системах отсчета. Пусть в некоторой точке A с координатой x, покоящейся относительно системы К, происходит событие, длительность которого (разность показаний часов в конце и начале события) τ = t2 - t1, где индексы 1 и 2 соответствуют началу и концу события. Длительность этого же события в системе К'
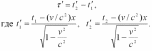
Таким
образом,
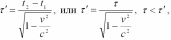 т.е.
длительность
события, происходящего в некоторой
точке, наименьшая в той инерциальной
системе отсчета, относительно которой
эта точка неподвижна. Следовательно,
часы, движущиеся относительно инерциальной
системы отсчета, идут медленнее покоящихся
часов,
т.е. ход часов замедляется в системе
отсчета, относительно которой часы
движутся.
т.е.
длительность
события, происходящего в некоторой
точке, наименьшая в той инерциальной
системе отсчета, относительно которой
эта точка неподвижна. Следовательно,
часы, движущиеся относительно инерциальной
системы отсчета, идут медленнее покоящихся
часов,
т.е. ход часов замедляется в системе
отсчета, относительно которой часы
движутся.
3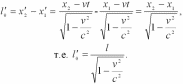 .
Длина
тел в разных системах отсчета.
Рассмотрим стержень, расположенный
вдоль оси x'
и покоящийся относительно системы К'.
Длина стержня в системе К'
равна l'0
= x'2
- x'1,
где x'1,
x'2
- не изменяющиеся со временем t'
координаты начала и конца стержня;
индекс 0 показывает, что в системе K'
стержень покоится. Определим длину
стержня в системе K,
относительно которой он движется со
скоростью v.
Для этого необходимо измерить координаты
концов стержня x1
и x2
в системе K
в один и тот же момент времени t.
Их разность l
= x'2
- x'1
и даст длину стержня в системе К:
.
Длина
тел в разных системах отсчета.
Рассмотрим стержень, расположенный
вдоль оси x'
и покоящийся относительно системы К'.
Длина стержня в системе К'
равна l'0
= x'2
- x'1,
где x'1,
x'2
- не изменяющиеся со временем t'
координаты начала и конца стержня;
индекс 0 показывает, что в системе K'
стержень покоится. Определим длину
стержня в системе K,
относительно которой он движется со
скоростью v.
Для этого необходимо измерить координаты
концов стержня x1
и x2
в системе K
в один и тот же момент времени t.
Их разность l
= x'2
- x'1
и даст длину стержня в системе К:
Таким
образом, размер тела, движущегося
относительно инерциальной системы
отсчета, уменьшается в направлении
движения в
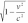 раз,
т.е. лоренцево
сокращение длины тем больше, чем больше
скорость движения.
раз,
т.е. лоренцево
сокращение длины тем больше, чем больше
скорость движения.
4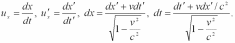 .
Релятивистский
закон сложения скоростей.
Пусть материальная точка движется в
системе К'
вдоль оси x',
а система К'
движется относительно К
со скоростью v
(оси x
и x'
совпадают). Тогда
.
Релятивистский
закон сложения скоростей.
Пусть материальная точка движется в
системе К'
вдоль оси x',
а система К'
движется относительно К
со скоростью v
(оси x
и x'
совпадают). Тогда
Произведя вычисления, получим релятивистский закон сложения скоростей:
Е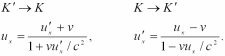 сли
скорости v,
u'x,
ux
малы по сравнению со скоростью света,
то эти формулы переходят в привычный
закон сложения скоростей в классической
механике. Релятивистский закон сложения
скоростей не противоречит второму
постулату Эйнштейна: если u'x
= c
то ux
= c,
т.е. скорость с
– предельная скорость, которую невозможно
превысить.
сли
скорости v,
u'x,
ux
малы по сравнению со скоростью света,
то эти формулы переходят в привычный
закон сложения скоростей в классической
механике. Релятивистский закон сложения
скоростей не противоречит второму
постулату Эйнштейна: если u'x
= c
то ux
= c,
т.е. скорость с
– предельная скорость, которую невозможно
превысить.
19. Релятивистская динамика, масса, импульс, энергия Закон взаимосвязи массы и энергии
Релятивистская масса
Согласно
представлениям классической механики
масса тела есть величина постоянная.
Однако в конце XIX столетия на опытах с
быстро движущимися электронами было
установлено, что масса тела возрастает
с увеличением скорости по закону:
 ,
(17)
,
(17)
где
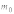 -
масса покоя.
-
масса покоя.
Н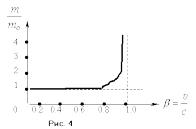 а
рис. 4 представлена зависимость
а
рис. 4 представлена зависимость
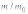 от
V/c.
от
V/c.
