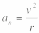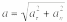- •Кинематика движения материальной точки Радиус-вектор, траектория перемещение, путь скорости, ускорение Нормальное тангенциальное полное ускорение
- •2. Кинематика движения по окружности Угловые характеристики движения Связь между линейными и угловыми характеристиками
- •3. Динамика поступательного движения материальной точки Законы Ньютона Инерциальные системы отсчета Принцип относительности Галилея преобразования Галилея
- •4 . Импульс Закон сохранения импульса.
- •5. Динамика твердого тела поступательное и вращательное движение Понятие момента силы и момента импульса относительно точки и неподвижной оси
- •6.Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси
- •7. Понятие момента инерции твердого тела Пример расчета Теорема Штейнера
- •Свободные затухающие колебания Дифференциальное уравнение, его решение Характеристики затухания.
- •Релятивистский импульс
Кинематика движения материальной точки Радиус-вектор, траектория перемещение, путь скорости, ускорение Нормальное тангенциальное полное ускорение
Р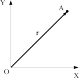 адиус-вектор
точки - это называется вектор,
начало которого совпадает с началом
системы координат, а конец - с данной
точкой.
Таким образом, особенностью
радиус-вектора,
отличающего его от всех других векторов,
является то, что его начало всегда
находится в точке начала координат
(рис. 17).
адиус-вектор
точки - это называется вектор,
начало которого совпадает с началом
системы координат, а конец - с данной
точкой.
Таким образом, особенностью
радиус-вектора,
отличающего его от всех других векторов,
является то, что его начало всегда
находится в точке начала координат
(рис. 17).
Введение понятия радиус-вектора оказалось чрезвычайно плодотворным при изучении различных физических явлений.
Траекто́рия
материа́льной то́чки
— линия
в пространстве,
представляющая собой множество
точек, в которых находилась, находится
или будет находиться материальная
точка
при своём перемещении в пространстве.
Перемеще́ние
(в кинематике) —
изменение местоположения физического
тела в пространстве
относительно выбранной системы
отсчёта.
Ускоре́ние
(обычно обозначается
 ,
в теоретической
механике
,
в теоретической
механике
 ) —
производная скорости
по времени, векторная
величина, показывающая, на сколько
изменяется вектор скорости
точки (тела) при её (его) движении за
единицу времени.
) —
производная скорости
по времени, векторная
величина, показывающая, на сколько
изменяется вектор скорости
точки (тела) при её (его) движении за
единицу времени.
.
Составляющая ускорения, направленная
вдоль скорости, называется тангенциальным
ускорением
|
|
|
|
Составляющая
ускорения, направленная к центру
кривизны траектории, т.е. перпендикулярно
(нормально) скорости, называется
нормальным
ускорением
|
|
|
|
Здесь R - радиус кривизны траектории в данной точке.
Тангенциальное
и нормальное ускорение взаимноперпендикулярны,
поэтому модуль полного ускорения .
|
|
|
2. Кинематика движения по окружности Угловые характеристики движения Связь между линейными и угловыми характеристиками
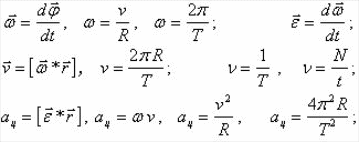
Вращение
твердого тела, как целого характеризуется
углом
 ,
измеряющегося в угловых
градусах или радианах,
угловой
скоростью
,
измеряющегося в угловых
градусах или радианах,
угловой
скоростью
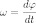 (измеряется
в рад/с) и угловым
ускорением
(измеряется
в рад/с) и угловым
ускорением
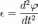 (единица
измерения - рад/с²).
(единица
измерения - рад/с²).
При равномерном вращении (T оборотов в секунду),
Частота вращения — число оборотов тела в единицу времени.
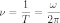 ,
,
Период вращения — время одного полного оборота. Период вращения T и его частота
 связаны
соотношением
связаны
соотношением
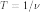 .
.
Линейная скорость точки, находящейся на расстоянии R от оси вращения
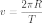 ,
,
Угловая скорость вращения тела
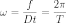 .
.
3. Динамика поступательного движения материальной точки Законы Ньютона Инерциальные системы отсчета Принцип относительности Галилея преобразования Галилея
Первый закон Ньютона-Тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны упругих тел не заставит его изменить это состояние.
Второй закон Ньютона - Если равнодействующая приложенных к телу сил не равна нулю, то тело движется с ускорением, величина которого прямо пропорциональна силе и обратно пропорциональна массе этого тела.
Третий закон Ньютона - При взаимодействии двух тел сила противодействия равна силе действия с обратным знаком.
Инерциальные системы отсчета – это системы, относительно которых материальная точка при отсутствии на нее внешних воздействий или их взаимной компенсации покоится или движется равномерно и прямолинейно. Инерциальными являются и системы отсчета, которые движутся равномерно и прямолинейно относительно какой-либо инерциальной системы отсчета. Галилей установил, что никакими механическими опытами, поставленными внутри инерциальной системы отсчета, невозможно установить, покоится эта система или движется равномерно и прямолинейно. Это утверждение носит название принципа относительности Галилея или механического принципа относительности.

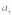 .
Она характеризует изменение скорости
по модулю.
.
Она характеризует изменение скорости
по модулю.
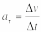
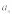 .
Она характеризует изменение скорости
по направлению.
.
Она характеризует изменение скорости
по направлению.