5. Методы решения уравнений

ЭЛЛИПТИЧЕСКОГО ТИПА

Многомерные уравнения эллиптического типа описывают стационарные процессы, и могут рассматриваться как частные случаи параболических уравнений при стремлении времени решения последних к бесконечности. Поэтому на практике для решения эллиптических уравнений полностью применимы методы, разработанные для решения уравнений параболического типа. Однако такие методы требуют значительных затрат машинного времени. Для решения краевых задач, описываемых эллиптическими уравнениями, чаще используются методы, специально разработанные для решения таких задач.

Все методы решения эллиптических уравнений можно разделить на аналитические и численные. Аналитические методы позволяют получить математически строгое решение. Однако круг решения задач с использованием этих методов весьма ограничен, и в настоящее время основными методами решения краевых задач с эллиптическими уравнениями являются численные методы. Эти методы также предполагают замену аналитических функций числовыми полями, над которыми производятся математические операции. В результате аппроксимации бесконечно малых величин операторов конечными приходят к системе алгебраических уравнений, которые решаются известными методами. Все методы решения систем алгебраических уравнений, аппроксимирующих эллиптические уравнения, можно разделить на две большие группы: прямые и итерационные.

Прямые методы позволяют решать системы алгебраических уравнений, с использованием конечного числа математических операций. При этом погрешность решения системы определяется погрешностью округления ЭВМ и может быть уменьшена специальными методами.

Итерационные методы можно рассматривать как специальным образом организованный переходный процесс. Используя начальное приближение и систему алгебраических уравнений, процесс решения системы строится таким образом, чтобы на каждой последующей итерации погрешность решения уменьшалась. Полученное решение всегда является приближённым, а время решения определяется заданной точностью.

5.1. Метод разделения переменных

Метод разделения переменных известен давно и применялся для решения уравнений Лапласа и Пуассона. Однако широкое распространение метод получил в последнее время в связи с разработкой быстрого преобразования Фурье (БДПФ)[23,27,32,33].

Идея быстрого преобразования Фурье заключается в следующем. Пусть на интервале имеет место разложение функции в дискретный ряд Фурье

; (5.1)

.

Если применять непосредственное вычисление с использованием приведённой формулы, то число математических операций, необходимых для расчёта окажется пропорциональным . Действительно, вначале необходимо вычислить значения , затем вычислить произведения , а затем просуммировать полученные произведения. Быстрое преобразование Фурье использует симметричность синусоидальных функций: sin 0=sin 180⁰ ; sin 15⁰ =sin 165⁰; sin 30⁰ =sin 150⁰; sin 45⁰ =sin 135⁰ и т.д. Вместо того, чтобы непосредственно выполнять умножение в выражении (5.1), рационально вначале вынести в нём общие множители, в результате чего число членов суммы сократится приблизительно в два раза. В получившемся ряду снова отыскиваются одинаковые множители, выносят их, сокращая в дальнейшем число членов разложения и т. д. И лишь, сократив до минимума число членов разложения, производят вычисление оставшихся произведений.

Наибольший выигрыш в уменьшении числа математических операций будет в том случае, если число членов разложения является степенью числа Однако ЭВМ оперируют с числами, представленными в двоичной системе счисления. Для реализации БДПФ число членов разложение принимают кратным степени . В общем случае решение дифференциальных уравнений методом разделения переменных с использованием БДПФ требует затрат математических операций, где -число интервалов разбиения пространственной координаты. Эффективность метода возрастает с увеличением числа . Так, при число операций пропорционально 1024, если коэффициенты разложения непосредственно вычислять по выражению (5.1), и 32×log₂32=160 при использовании БДПФ. Число математических операций уменьшается в 1024/160=6,4 раза. Если число увеличить до 128, то соответствующие значения составляют 128²=16384 и 28×log₂128=896, и число операций уменьшается в 16384/896=18,28 раз. Учитывая слабую зависимость логарифмической функции от аргумента, можно утверждать, что БДПФ по скорости реализации лишь незначительно уступает наиболее быстрому методу прогонки [27].

Метод разделения переменных предполагает разложение искомой функции и правой части дифференциального уравнения по собственным функциям дискретного оператора Лапласа, удовлетворяющие уравнению

(5.2)

при нулевых граничных условиях ; .

Значения l, удовлетворяющие этому уравнению, называются собственными значениями.

Исследуемую область разбивают на интервалов величиной . Решение краевой задачи ищем в виде , коэффициент которого a определяется из граничных условий.

Запишем значения функций для точек и с координатами и соответственно

; . (5.3)

Заменяя производную в уравнении (5.2) конечно-разностным оператором, будем иметь

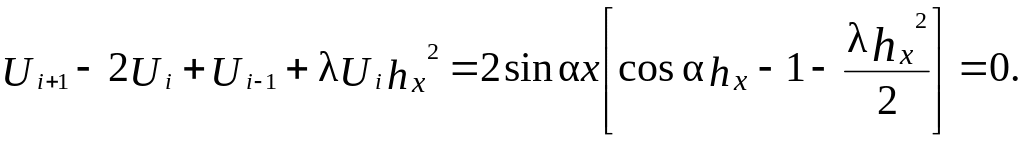(5.4)

Поскольку находится нетривиальное решение , то

, (5.5)

откуда собственное значение

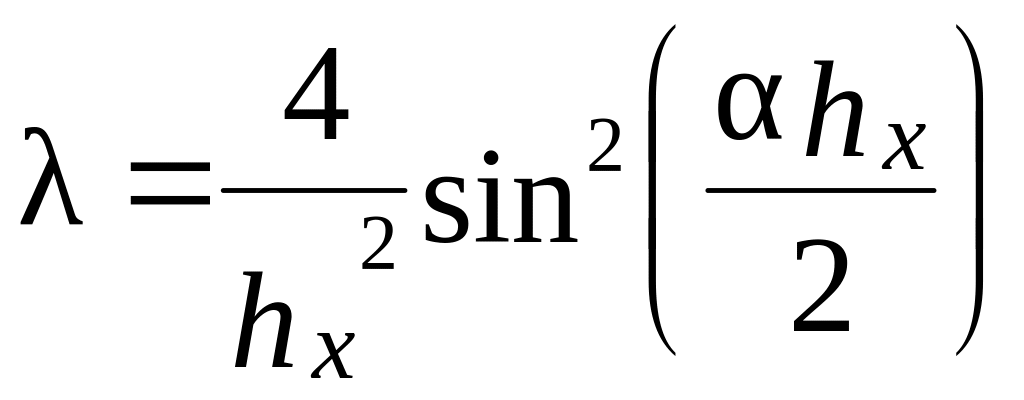. (5.6)

Определим a, используя граничные условия. При граничное условие выполняется всегда. Второе граничное условие при выполняется в том случае, если , где -целое число. Отсюда определяется

. (5.7)

Если и , то собственные функции

, (5.8)

а собственные значения

. (5.9)

Таким образом, собственные функции дискретного оператора Лапласа описываются выражениями

,

а собственные значения -

.

Все собственные значения положительны и лежат в диапазоне

;

Собственные функции ортогональны на интервале [0,L], а их норма равна

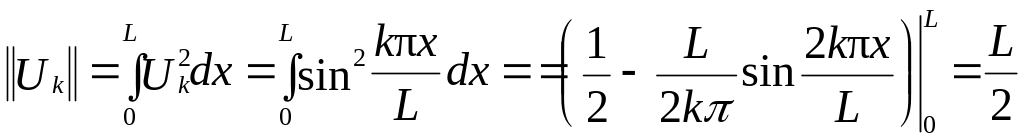. (5.10)

В этом случае собственные функции с учётом нормировки записываются в виде

, (5.11)

В работах [18, 23, 25, 27, 32, 33 ] показано, что финитную функцию можно представить в виде разложения по собственным функциям дискретного оператора Лапласа

, (5.12)

где коэффициенты разложения

. (5.13)

Рассмотрим метод разделения переменных при решении двумерного уравнения Пуассона при нулевых граничных условиях первого рода

(5.14)

или

(5.15)

где и -одномерные операторы Лапласа.

Будем рассматривать искомую функцию и правую часть уравнения как функции сеточного аргумента и . Поскольку обе функции обращаются на границах исследуемой области в нуль, их можно разложить по собственным функциям дискретного оператора Лапласа, например

; ; . (5.16)

; ; . (5.17)

. (5.18)

Подставляя выражения для и в уравнение (5.15), получим

. (5.19)

или

. (5.20)

Поскольку не зависит от координаты , эту собственную функцию можно вынести за знак производной по . Аналогично, не зависит от координаты . Поэтому эту функцию также можно вынести за знак производной по . Тогда будем иметь

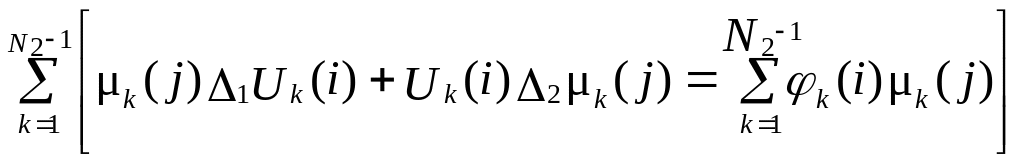. (5.21)

Собственные функции дискретного оператора Лапласа , как показано выше, находятся при решении уравнения

. (5.22)

Отсюда следует

. (5.23)

Подставляя полученное выражение в (5.21), будем иметь

. (5.24)

В силу ортогональности собственных функций дискретного оператора Лапласа указанное равенство выполняется для каждого члена разложения. Тогда

. (5.25)

для , краевых условиях и собственных значениях оператора

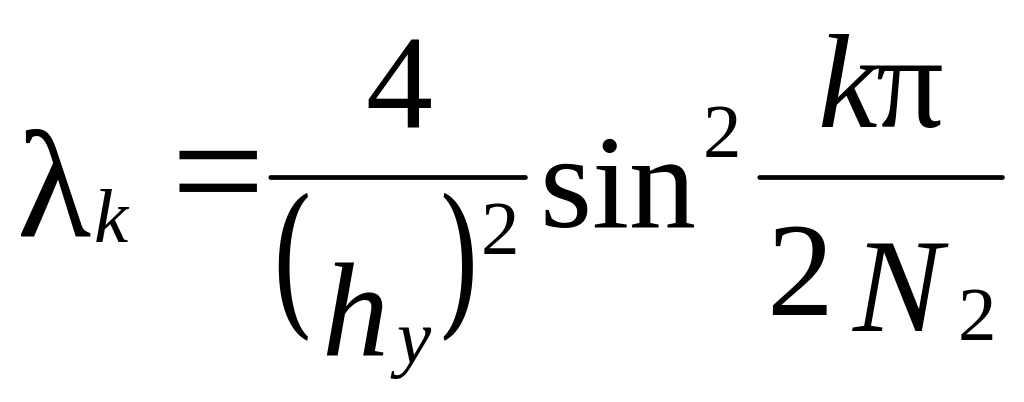. (5.26)

Таким образом, для каждого члена разложения решается одномерная краевая задача (5.25) с использованием прогонки по при минимальном числе математических операций. Рассчитав , можно по выражению (5.16) восстановить искомую функцию во всех точках исследуемой области. Нахождение коэффициентов разложения и восстановление искомой функции производится с использованием БДПФ с минимальной затратой математических операций. Подобный подход распространяется и на решение многомерных краевых задач с уравнениями Пуассона, а также других, более сложных задач, допускающих разделение переменных. В качестве одномерного в этом случае может быть взят оператор вида

, (5.27)

т.е. оператор, коэффициенты которого зависят лишь от одной пространственной переменной. Полученная краевая задача с указанным оператором также решается методом прогонки.

Решение уравнений Лапласа и Пуассона методом разделения переменных с использованием БДПФ является самым быстрым и точным способом решения этих уравнений.

Уравнения Лапласа и Пуассона могут быть решены методом редукции. Идея метода заключается в том, чтобы постепенно понижать порядок системы, исключая последовательно сначала неизвестные с нечётными номерами, затем неизвестные с номерами, кратными двум, затем - кратными четырём, восьми и т. д.

Если число неизвестных кратно 2^к, то в результате последовательного исключения остаётся одно уравнение, из которого можно найти неизвестное с номером . После этого осуществляется обратный ход, в результате которого вычисляются значения неизвестных с номерами .

Метод редукции по числу вычислительных операций сравним с методом разделения переменных, т.е. , однако имеет более сложный алгоритм реализации. Описание этого метода и его использование для решения краевых задач можно найти в [27, 32, 33].

Рассмотрим использование метода разделения переменных для решения двумерной краевой задачи из предыдущего раздела (пример № 5).

Пример № 11

Решение двумерной краевой задачи

методом разделения переменных