V2: Средние величины. Структурные средние

I: k = A

S: Средняя величина характеризует _________

+: всю совокупность в целом одним числом

-: варианту, стоящую в середине ранжированного ряда

-: каждую конкретную единицу

-: объем вариационного ряда

I: k = A

S: Какая средняя применяется, если значение признака встречается несколько раз ______

+: средняя арифметическая взвешенная

-: средняя арифметическая простая

-: средняя геометрическая

-: средняя гармоническая

I: k = A

S: Укажите формулу средней арифметической взвешенной

-: =

+: =

-:

-:

I: k = A

S: Имеются данные о месячной заработной плате пяти рабочих:

6000; 7500; 8000; 6500; 9500 тыс руб. Определить среднюю заработную плату

+: 7500

-: 8000

-: 6500

-: 6300

I: k = A

S: Какая средняя применяется в тех случаях, если частоты не приводятся непосредственно, а входят сомножителями в один из имеющихся показателей

-: средняя арифметическая простая

-: средняя геометрическая

+: средняя гармоническая

-: средняя хронологическая

I: k = A

S: Определите модальный интервал

80 - 100 - 3

100 - 120 -13

120 – 140 -15

140 – 160 -20

160 – 180 - 8

180 – 200 - 1

-: 80 - 100 - 3

-:100 - 120 -13

-:120 – 140 -15

+:140 – 160 -20

I: k = A

S: Медианой называется ________

+: серединная варианта упорядоченного вариационного ряда

-: наибольшая частота

-: варианта, которая чаще других встречается

-: медианный интервал

I: k = A

S: Медианой данного нечетного ряда :

156, 158, 160, 161, 166, 168, 172 является:

+: 161

-: 160

-: 168

-: 158

I: k = A

S: Средний квадрат отклонения всех значений признака ряда распределения от средней арифметической, называется ________

+: дисперсией

-: коэффициентом вариации

-: средним квадратичным отклонением

-: средней гармонической

I: k = A

S: Укажите формулу простого среднего квадратического отклонения

-: σ =

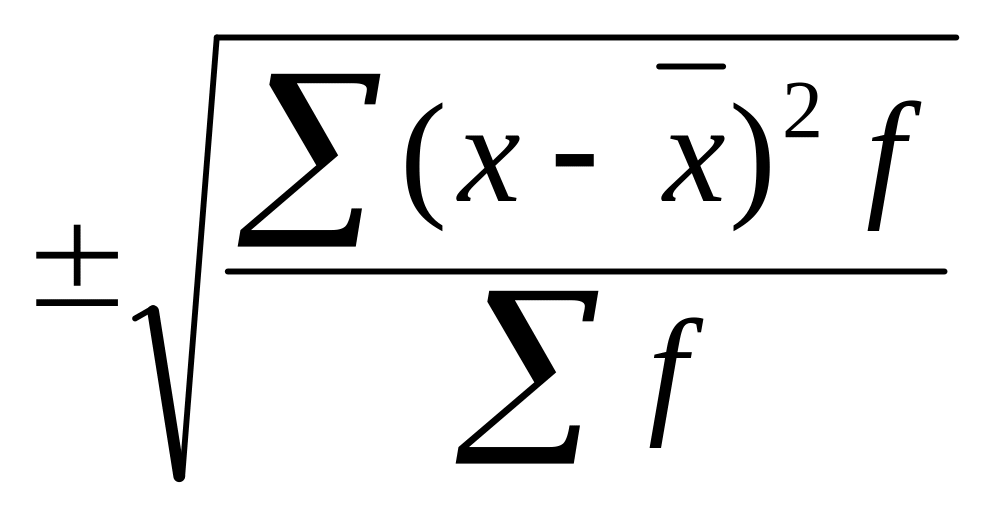
-: σ =

+: σ =

-: σ =

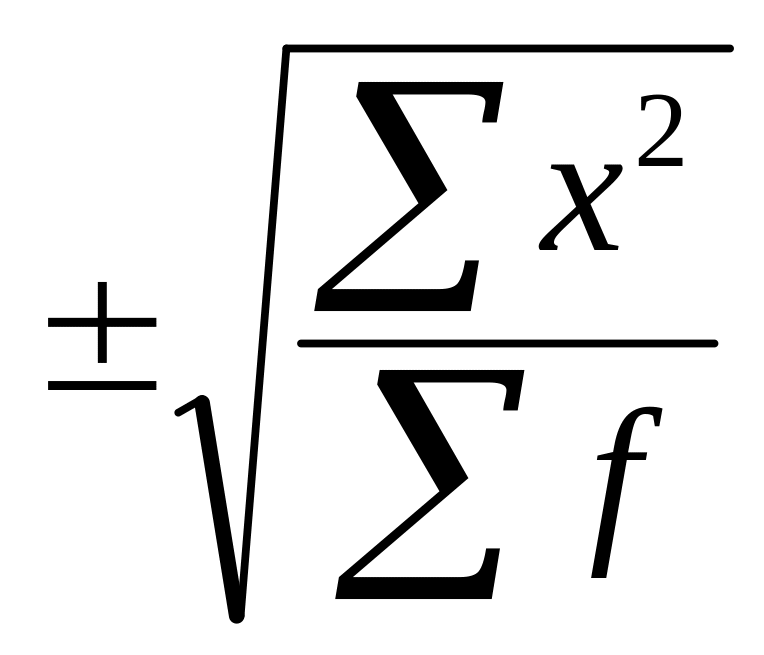
I: k = A

S: Внутригрупповая дисперсия характеризует…

+: часть вариации, происходящую под влиянием неучтенных в данной группировке факторов

-: вариацию признака под влиянием всех обусловивших ее факторов

-: вариацию признака под влиянием результативного показателя

-: вариацию признака под влиянием группировочного показателя

I: k = A

S: В случае если имеются данные о значении дисперсии, можно рассчитать значение_________________

+:среднего квадратического отклонения

-: размаха вариации

-: среднего линейного отклонения

-: коэффициента вариации

I: k = A

S: Общая дисперсия характеризует…

+: вариацию признака под влиянием всех обусловивших ее факторов

-: вариацию признака под влиянием группировочного показателя

-: часть вариации, происходящую под влиянием неучтенных в данной группировке факторов

-: вариацию признака под влиянием результативного показателя

I: k = A

S: Если коэффициент вариации составляет 45%, то совокупность…

+:неоднородная

-: умеренной однородности

-: средней однородности

-: однородная

I: k = A

S: Модой в ряду распределения является_________________

+: варианта, которая чаще других встречается

-: наибольшая частота

-: варианта, делящая ряд ранжированных значений на две равные части

-: модальный интервал

I: k = A

S: Размахом вариации называется_______________максимального и минимального значений признака

+: разность

-: произведение

-: частное от деления

-: сумма

I: k = A

S: Согласно правилу сложения дисперсий общая дисперсия равна ________________ межгрупповой дисперсии и средней из внутригрупповых дисперсий

+: сумме

-: разности

-: частному отделения

-: произведению

I: k = A

S: В теории статистики для графического представления интервального вариационного ряда используют следующие виды диаграмм…

+: полигон

+: гистограмма

-: секторная диаграмма

-: круговая диаграмма

I: k = A

S: К абсолютным показателям вариации относят…

+: размах вариации

+: среднее линейное отклонение

+: дисперсию

-: коэффициент корреляции

-: коэффициент вариации

I: k = A

S: Каждая варианта уменьшена в 6 раз, вес каждой варианты уменьшен в 2 раза. Средняя величина в этом случае…

+: уменьшится в 6 раз

-: увеличится в 6 раз

-: уменьшится в 12 раз

-: уменьшится в 3 раза

I: k = A

S: К видам дисперсий относят…

+: межгрупповую

+: внутригрупповую

+: общую

-: интервальную

-: параметрическую