5.Аффинные преобразования в трехмерном пространстве. Масштабирование, перенос, однородные координаты.

Аффинные преобразования в трехмерном пространстве:

Для выполнения пространственных построений, аналогично двумерной задаче, три координаты точки (x, y, z) заменяются четверкой чисел (x, y, z, 1). Это дает возможность воспользоваться матричной записью и в более сложных трехмерных задачах.

Любое аффинное преобразование в трехмерном пространстве может быть представлено в виде суперпозиции вращений, растяжений, отражений и переносов. Математически все преобразования сводятся к перемножению матриц четвертого порядка.

Перенос:

В ходе обработки модели, часто, возникает необходимость перенести объект не изменяя его формы и размеров, такое перемещение обычно задается вектором, называемым вектором переноски. Его направление определяет направление переноса, а проекции на координатные оси задают перемещение вдоль этих осей.

Однородные координаты:

Определить такое преобразование с использованием матрицы размером 2*2 невозможно. Преодолеть данную трудность можно с помощью перехода в однородные координаты, точка на плоскости в однородных координатах определяется тройкой [X Y W] где W – масштабирующий коэффициент, X Y – координаты точек, получаемые из декартовых по средствам следующих соотношений.

X = x*W

Y = y*W

По однородным координатам с помощью деления на масштабирующий коэффициент всегда можно найти декартовую координату. Очевидно, что этот коэффициент не должен быть равен нулю. Однородные координаты не обладают однозначностью, т.е. точка [1 3 1], [2 6 2], [3 9 3] - будет одна и та же точка.

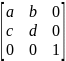
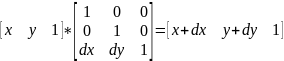
Масштабирование:

Коэффициенты сжатия/растяжения, по аналогии с двухмерным пространством, определяются диагональными членами матрицы R:

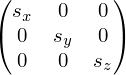
Результат:

Комбинация коэффициентов s_x = -1, s_y = 1, s_z = 1 будет задавать отражение от плоскости Oyz (x = 0). При s_x = s_y = s_z = -1 получим центральную симметрию относительно начала координат.

6.Аффинные преобразования в трехмерном пространстве. Повороты. Композиция преобразований.

Аффинные преобразования в трехмерном пространстве:

Для выполнения пространственных построений, аналогично двумерной задаче, три координаты точки (x, y, z) заменяются четверкой чисел (x, y, z, 1). Это дает возможность воспользоваться матричной записью и в более сложных трехмерных задачах.

Любое аффинное преобразование в трехмерном пространстве может быть представлено в виде суперпозиции вращений, растяжений, отражений и переносов. Математически все преобразования сводятся к перемножению матриц четвертого порядка.

Преобразование поворотов:

Если 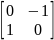– поворот

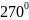
Если 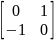– поворот

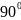
Если 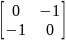– поворот

Рисунок в лекциях.

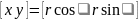
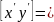
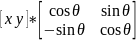
Композиция преобразования

Общая схема произвольных преобразований:

С помощью поворота преобразовать исходную схему, так чтобы требуемое произвольное преобразование свелось к известному преобразованию. Далее выполняется известное преобразование. Применить к сцене обратно сделанное преобразование в пункте один.

Одной из главных причин использования преобразования в матричной форме, является возможность получать сложные матрицы путем композиции более простых матриц.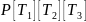

[M]-композиция матриц

Выводы по плоским геометрическим преобразованиям.

Для всех двумерных изображений потребуется матрица 3*3.

Элементы:

a b c d – определяют коэффициенты поворота, масштабирования и сдвига;

e f – служат для формирования переноса;

s – коэффициент общего масштабирования;

k m – обычно задаются нулями, служат для создания проекции, например перспективной