В координатах p,V и t,s

Таблица 3

Соотношения между изменениями внутренней энергии, теплоты

и работы в политропных процессах расширения

Номер зоны	Интервал изменения п	dT	du=сvdT	Δq=Tds	с= δq/dT	Соотношение между энергетическими эффектами
1						Подводимая q идёт на выполнение l и увеличение u
2						Работа l выполняется за счёт подводимой q и уменьшения u
3						За счёт уменьшения u выполняется работа l и отводится q

2. Цикл с политропным расширением, изобарным сжатием и изохорным подводом теплоты

Выполним расчёт и анализ указанного цикла на примере решения следующей задачи.

Задача. 11 м³ криптона политропно расширяется до 1/4 первоначального давления, затем изобарно сжимается до первоначального объема, наконец, изохорно возвращается в исходное состояние. Начальные параметры рабочего тела: давление р₁ = 0,2 МПа и температура t₁ = 350 °С. Показатель политропы расширения n = 2.

Определить параметры рабочего тела в характерных точках указанной совокупности процессов, суммарные значения теплоты и работы заданного количества криптона в цикле, а также изменения удельных:

• внутренней энергии в политропном процессе 1-2;

• энтропии в изобарном процессе 2-3;

• энтальпии в изохорном процессе 3-1 (рис. 1.2).

Изобразить указанный цикл в термических и тепловой диаграммах.

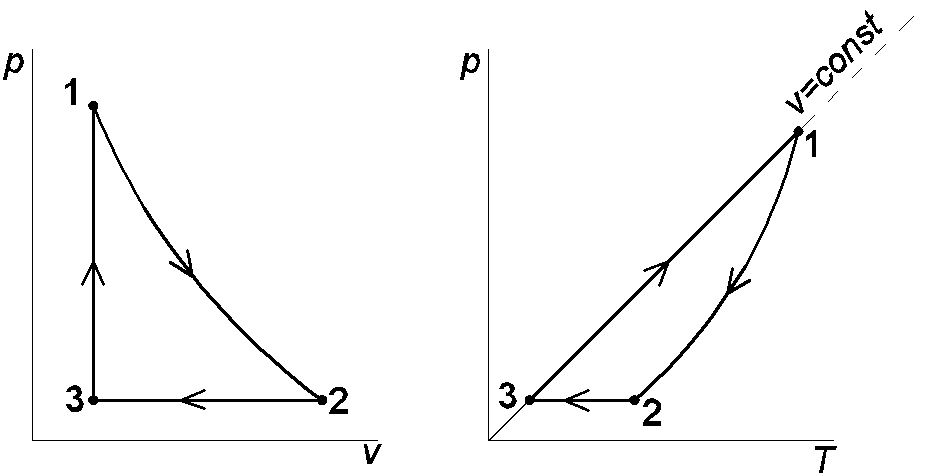
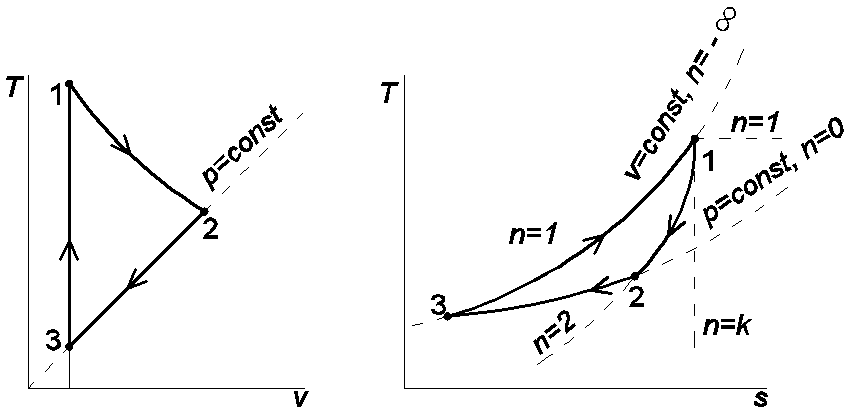
Рис.1.2. Изображения заданной совокупности процессов на термических

И тепловой диаграммах:

1-2 – политропное расширение; 2-3 – изобарное сжатие;

3-1 – изохорный подвод теплоты

Решение

Криптон (Kr) – одноатомный газ, поэтому его показатель адиабаты k = 1,6667. По таблице Менделеева определяем молекулярную массу криптона: _Kr = 83,8 кг/кмоль.

Удельная газовая постоянная криптона

.

Масса криптона, участвующего в заданной совокупности процессов (цикле), определяем из уравнения Клапейрона для М кг рабочего тела в идеально-газовом состоянии

.

Рассчитываем термические параметры рабочего тела в характерных точках цикла.

Точка 1

• абсолютная температура в Кельвина

Т₁ = t₁°С+273,15 = 350 +273,15 = 623,15К;

• удельный объем в начальной точке цикла определяем из уравнения Клапейрона для 1 кг идеального газа рv = RT

.

Точка 2

Процесс 1-2 – политропный, поэтому в нём изменяются все три термических параметра состояния в соответствии с соотношением

.

Так как по условию задачи р₁/р₂ = 4, то р₂ = р₁/4 = 0,2/4 = 0,05 МПа, тогда

.

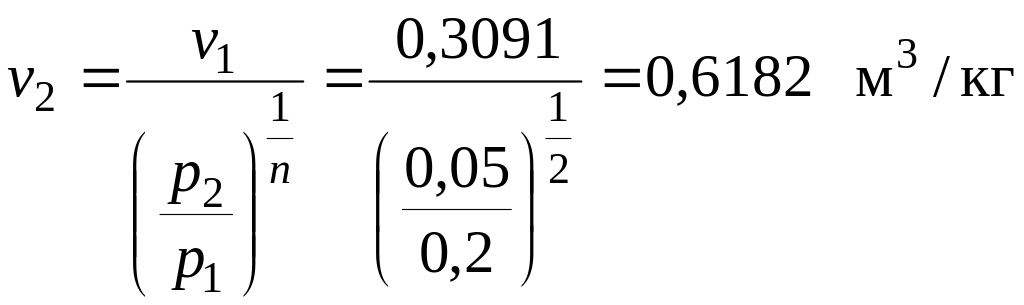Температуру в точке 2 рассчитываем из приведенного выше соотношения

.

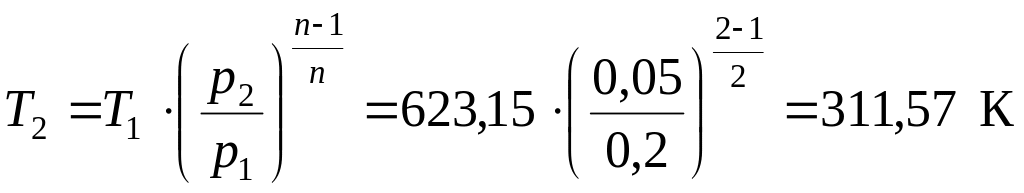Для проверки рассчитываем значение Т₂ из уравнения состояния

.

Точка 3

Процесс 2-3 – изобарный, поэтому р₃ = р₂ = 0,05 МПа.

Соотношение между параметрами в изобарном процессе

 тогда .

По условию задачи v₃ = v₁ = 0,3091 м³/кг.

Результаты расчетов записываем в таблицу:

Номера точек	р, Мпа	v, м3/кг	Т, К
1	0,2	0,3091	623,15
2	0,05	0,6182	311,59
3	0,05	0,3091	155,80

Рассчитываем количество удельной теплоты, подводимой (отводимой) в заданных процессах.

В политропном процессе 1-2

,

где c_v – изохорная теплоемкость. По упрощенной молекулярно-кинетической теории МКТ c_v=(3+j)·R/2; здесь j – количество различимых вращательных степеней свободы атомов в молекуле. Криптон одноатомный газ, поэтому j = 0

.

Поскольку рассчитанное значение q_1-2 < 0, в процессе 1-2 теплота отводится от рабочего тела в окружающую среду.

В изобарном процессе 2-3

,

где с_p = (5+j)R/2 = 2,5R = 2,5·0,0992 = 0,2480 кДж/(кг·К) – изобарная теплоёмкость.

Так как q_2-3<0, то и в этом процессе теплота отводится.

В изохорном процессе 3-1

.

Следовательно, в этом процессе теплота подводится.

Суммарное количество теплоты, подводимой (отводимой) в цикле:

– удельное (для 1 кг рабочего тела)

;

– общее (для М кг рабочего тела)

.

Следовательно, теплоты подводится больше, чем отводится. Разность подводимой и отводимой теплоты (549,87 кДж) в рассматриваемом цикле превращается в работу.

Определяем значения удельных работ, получаемых (затрачиваемых) в процессах цикла:

— в политропном процессе расширения 1-2

,

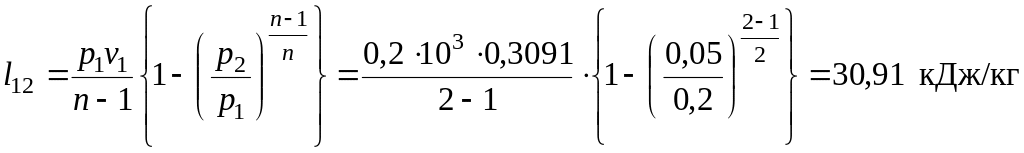— в изобарном процессе сжатия 2-3

.

— в изохорном процессе нагрева 3-1

.

Суммарное количество работы, полученной в цикле:

– удельное (работа 1 кг газа)

;

– общее (работа М кг газа)

.

Результаты расчетов значений теплоты и работы сводим в таблицу

Процессы	Теплота, q	Деформационная работа, l
1-2 – политропный процесс Расширения	–15,45	30,91
2-3 – изобарный процесс сжатия	–38,64	–15,46
3-1 – изохорный процесс подвода теплоты	69,55	0
Сумма	15,45	15,45

Изменение внутренней энергии в политропном процессе расширения 1-2

кДж/кг.

Проверка.

Из первого закона термодинамики следует

.

Из выполненных расчетов следует, что в политропном процессе расширения 1-2 работа совершается за счет внутренней энергии. Кроме того, часть внутренней энергии (15,45 кДж/кг) отводится в окружающую среду в виде теплоты.

Изменение энтропии в изобарном процессе 2-3

.

Поскольку Δs₂₃<0, теплота в этом процессе отводится, что подтверждается приведенными выше расчетами.

Изменение энтальпии в изохорном процессе 3-1

.

Проверка.

Из первого закона термодинамики следует

,

где техническая работа в изохорном процессе

.

В изохорном процессе подводимая теплота накапливается в виде внутренней энергии рабочего тела, что проявляется в повышении давления, так как dh = du+vdp.