3.7. Процесс течения

Основное уравнение термодинамики для стационарного (установившегося) потока, когда он не выполняет технической работы, имеет вид

, (3.1)

откуда

. (3.2)

Следовательно, в общем случае приращение кинетической энергии рабочего тела происходит за счёт уменьшения его энтальпии и подводимой извне теплоты.

С другой стороны, в [2] показано, что изменение кинетической энергии потока равно технической работе статического процесса расширения, уравнение которого совпадает с уравнением процесса, совершаемого движущимся элементом

. (3.3)

Приведенные уравнения справедливы как при наличии, так и при отсутствии в потоке трения, обусловливаемого силами вязкости, поскольку закон сохранения энергии, на основании которого получены эти уравнения, справедлив для любых процессов.

Течение без трения и теплообмена (обратимое или идеальное адиабатное течение) является изоэнтропным, и для него справедливо равенство

. (3.4)

Тогда скорость потока (м/с) на выходе из канала равна

, (3.5)

если значения энтальпии подставлять в Дж/кг. При истечении из сосуда большого объема (w₁=0) и при подстановке значений h в кДж/кг формула (3.5) преобразуется к виду

. (3.6)

На практике имеет место реальное (необратимое) адиабатное течение при наличии трения. Действительная скорость с учетом трения рассчитывается через скорость идеального течения

, (3.7)

где φ – скоростной коэффициент, определяемый по опытным данным. Он всегда меньше 1, зависит от рода движущегося вещества, степени шероховатости поверхности канала и других факторов. Для сопел паровых турбин значения φ находятся в пределах 0,95-0,98.

Поскольку любой необратимый процесс сопровождается ростом энтропии, поэтому на энтропийных диаграммах располагается правее вертикальной линии обратимого изоэнтропного процесса расширения s = idem и изображается штриховой линией, проведенной из общей начальной точки.

Из уравнений (3.4) и (3.7) при w₁ = 0 следует

, (3.8)

где > – действительное значение энтальпии в конце истечения при фиксированном значении р₂.

Из формулы (3.8) следует

, (3.9)

где – коэффициент потери энергии.

Итак, если на диаграмме h, s от начальной точки изоэнтропы расширения (1-2) отложить вниз отрезок φ²(h₁-h₂) либо от конечной точки 2 отложить вверх отрезок ζ·(h₁-h₂) и из полученной точки провести горизонтальную линию до пересечения с изобарой р₂, то точка их пересечения 2' будет соответствовать реальному конечному состоянию потока рабочего тела. Таким же образом можно определить положения промежуточных точек действительного процесса истечения рабочего тела (1-2^') (рис.3.13)

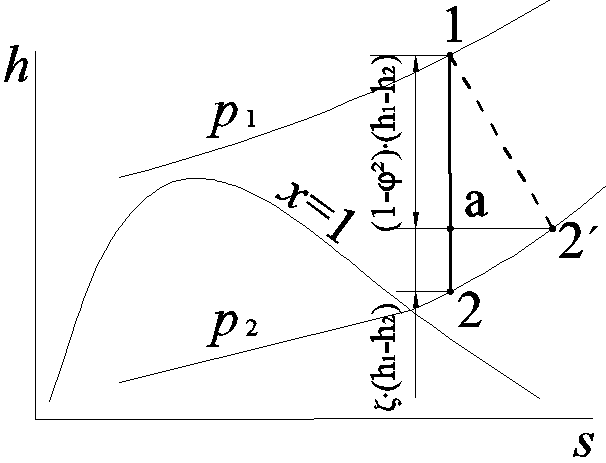
Рис. 3.13. Обратимый (1-2) и действительный (1-2’) процессы течения

рабочего тела на диаграмме h,s, где 1-а = (1-φ²)·(h₁- h₂), а 2-a = ζ(h₁ – h₂)

Для определения профиля канала, по которому движется поток, и для обеспечения заданного режима его движения необходимо рассмотреть вопрос о форме струи потока. В [2] на основании уравнения (3.3) получено соотношение между скоростью течения и поперечным сечением струи пара (газа) в дифференциальной форме

, (3.10)

где w/a = M – отношение скорости потока к местной скорости распространения звука в движущемся потоке (так называемое число Маха).

Из этого уравнения следует ряд важных выводов. Так, для увеличения скорости потока (dw > 0):

• при дозвуковых начальных скоростях потока (w < a или M <1) площадь струи должна уменьшаться (df < 0);

• при сверхзвуковых начальных скоростях потока (w>a или M >1) сечение струи должно увеличиваться (df > 0);

• для последовательного увеличения скорости потока от дозвуковых до сверхзвуковых значений, поперечное сечение струи сначала должно уменьшаться (df <0), а затем увеличиваться (df >0). При этом в минимальном сечении df = 0 и М = 1, то есть скорость потока равна местной скорости звука.

Естественно, профиль канала, по которому движется газообразное рабочее тело, должен соответствовать указанным формам струи во избежание потерь кинетической энергии потока.

Скорость звука в жидкостях существенно больше, чем в газах, поэтому течение жидкости всегда происходит при дозвуковых скоростях, и для увеличения скорости потока жидкости сечение канала должно уменьшаться (df < 0).

Для замедления потока газа, движущегося со сверхзвуковой скоростью (М >1), до дозвуковой скорости (М < 1) канал также должен иметь сначала сужающуюся, а затем расширяющуюся части.

При адиабатном течении с трением описанная выше форма струи сохраняется, но в расчетном минимальном сечении скорость потока отличается от местной скорости звука. Так, при ускорении движения потока сечение, в котором М = 1, смещается в расширяющуюся часть струи (канала).

Скорость потока, совпадающая с местной скоростью звука, называется критической, а давление газа (пара) в соответствующем сечении – критическим давлением истечения р_к (не путать с критическим давлением в критической точке состояния реального газа).

Отношение критического давления истечения р_к к давлению заторможенного потока в начальном сечении р₁ (где можно пренебречь начальной скоростью потока w₁), называется критическим отношением давлений β_к = p_к/p₁.

Если отношение конечного давления истечения (давления среды, в которую проходит истечение) р_а, к начальному давлению р₁, больше значения β_k (р_а/р₁ >β_к), то канал должен иметь только сужающуюся часть, в противном случае (при р_а/р₁<β_к) он должен иметь также расширяющуюся часть. Сопло, состоящее из сужающейся и расширяющейся частей, называется соплом Лаваля.

Для изоэнтропного течения идеального газа значение β_к определяется аналитически и зависит от числа атомов в молекуле:

• для двухатомных газов β_к = 0,528;

• для трехатомных газов β_к = 0,546.

Для водяного пара, как реального газа, β_к является переменной величиной, зависящей от начального термодинамического состояния потока:

• в области перегретого пара при умеренных давлениях β_к = 0,546;

• для насыщенного пара β_к = 0,577;

• для оценочных расчетов β_к можно принимать равным 0,5.

Профилирование сопла заключается в определении зависимости площади его поперечного сечения от длины сопла. Чаще всего расширяющаяся часть сопла имеет коническую форму. Угол раствора этой части γ не должен превышать 11-12 ° во избежание отрыва потока от стенок канала. Поэтому для определения длины расширяющейся части сопла, достаточно рассчитать значения диаметра минимального и максимального (выходного) сечений (d_min и d₂). Тогда длина расширяющейся части сопла определяется из соотношения

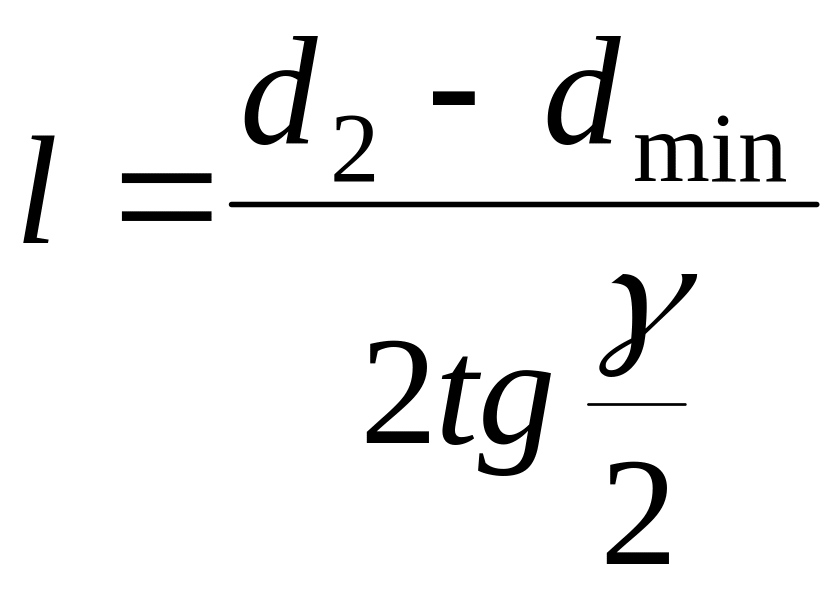. (3.11)

Сужающаяся часть сопла чаще всего не рассчитывается, а профилируется так, чтобы входной участок плавно сопрягался с минимальным сечением.

Площадь поперечного сечения рассчитывается из уравнения сплошности

. (3.12)

Скорость w определяется из уравнения (3.6) для идеального адиабатного течения потока либо по формуле (3.7) для течения с трением. Значения удельного объема пара (v) определяются по диаграммам либо таблицам термодинамических свойств рабочего тела.

Рассмотрим примеры решения задач, в которых рабочее тело (вода и водяной пар) совершают процесс истечения.

Задача 1

Определить форму канала и выходную скорость идеального адиабатного истечения водяного пара из сопла, если давление заторможенного потока р₁ = 2,0 МПа, температура – 400 °С. Давление среды, в которую происходит истечение пара, равно р_а = 0,01 МПа.

Решение

Определяем форму канала, которая обеспечит идеальное ускорение (без энергетических потерь) потока, движущегося под действием указанной разности давлений. Для этого определяем отношение

.

Поскольку β < β_к (для перегретого пара β_к = 0,546), сопло должно иметь сужающуюся и расширяющуюся части. Как отмечается выше, такой канал называется соплом Лаваля.

Скорость идеального истечения пара рассчитывается из соотношения

,

При решении задачи с помощью h,s диаграммы

где h₁ = 3246 кДж/кг – энтальпия пара в начале истечения (при р₁ = 2,0 МПа и 400 °С); точка 1 определяется на пересечении указанных изобары и изотермы.

h₂ = 2256 кДж/кг – энтальпия пара в конце истечения (при р₂ = 0,01 МПа); точка 2 определяется на пересечении изоэнтропы s₁=s₂ и изобары р₂.

Задачу можно (и нужно!) решить с помощью таблиц термодинамических свойств воды и водяного пара. По табл. ІІІ [3] стр.108 находим значения калорических свойств пара в начальной точке процесса: h₁ = 3248,1 кДж/кг, s₁ = 7,1285 кДж/(кг·К).

Значение энтропии в конце изоэнтропного процесса истечения s₂ = s₁ = =7,1285 кДж/(кг·К). Так как s₂< s'' = 8,1505 кДж/(кг·К) при давлении р₂ = 0,1 бар, то пар в конце истечения влажный. Тогда по [3] табл. ІІ стр.62 при р = 0,1 бар рассчитываем степень сухости и энтальпию пара в конце процесса истечения

.

Итак, скорость идеального истечения пара

.

Сопоставляя значения w₂, рассчитанные с помощью таблиц [3] и диаграммы h,s, можно сделать вывод, что они практически совпали.

Задача 2

Определить теоретическую скорость адиабатного истечения пара из отверстия трубопровода в атмосферу, если давление пара 1,0 МПа, а температура 500 °С. Как изменится скорость истечения, если при той же температуре давление пара в трубопроводе уменьшится до 0,16 МПа.

Решение

Давление среды, в которую происходит истечение – атмосферное, то есть р_а = 1 бар = 0,1 МПа. Тогда отношение р_а/р₁= 0,1, то есть значительно меньше критического β_к. Следовательно, для максимального ускорения потока пара при заданном соотношении давлений надо применить сопло Лаваля. Однако истечение происходит не из сопла Лаваля, поскольку в условии задачи сказано “адиабатное истечение из отверстия трубопровода”. Из диаграммы h,s следует, что процесс совершается в области перегретого пара, для которого можно принять значение β_к = 0,546 как для трехатомного газа. Тогда критическое давление истечения равно

.

Из теории известно, что если значение конечного давления истечения р_а меньше р_к, то не происходит максимально-возможное ускорение потока(выше критического), а происходит его завихрение при выходе из отверстия, то есть потеря энергии.

Тогда на пересечении изобары р₁ = 1,0 МПа и изотермы t₁ = 500 °С определяем положение точки 1 (начало процесса) и значение h₁ = 3476 кДж/кг. Проведя из точки 1 изоэнтропу до пересечения с изобарой р₂ = р_к = 0,546 МПа, определяем значение энтальпии в точке 2 – h₂ = 3278 кДж/кг.

Скорость идеального истечения пара из отверстия трубопровода равна

.

Во втором случае (при р₁ = 0,16 МПа и t₁ = 500 °С) процесс истечения также проходит в области перегретого пара, однако отношение р_а/р₁ = 0,1/0,16 = = 0,625 > β_к = 0,546. Следовательно, скорость истечения пара из отверстия меньше критической. Определив по диаграмме h,s значения h₁ =3488 кДж/кг и h₂ = 3328 кДж/кг, рассчитываем теоретическую скорость идеального истечения пара из отверстия

.

Уточним решение этой задачи с помощью таблиц термодинамических свойств воды и водяного пара [3].

В первом случае значения энтальпии и энтропии пара в начальном состоянии (при р₁ = 10 бар и t₁ = 500°С) равны: h₁ = 3478,3 кДж/кг, s₁= 7,7627 кДж/(кг·К) ([3] табл. ІІІ). Значение энтальпии пара при р_к = 5,46 бар определим из условия s₂ = s₁ = 7,7627 кДж/(кг·К) методом двойной интерполяции. Сначала интерполируем на изобарах р_м = 5,0 бар и р_б = 5,5 бар по энтропии s₂=7,7627 кДж/(кг·К), затем по давлению k_p= (5,46-5,0)/(5,5-5,0) = 0,92; в итоге получим h₂ = 3277,6 кДж/кг. Тогда скорость истечения

.

Во втором случае, когда давление пара в трубопроводе понизилось до 1,6 бар, значения энтальпии и энтропии пара в начальном состоянии (при р₁ = 1,6 бар и t₁ = 500 °С) равны h₁ = 3487,3 кДж/кг, s₁ = 8,6171 кДж/(кг·К). Значение энтальпии в конце процесса истечения в этом случае определяем из условия р₂ = 1 бар и s₂ = s₁ = 8,6171 кДж/(кг·К). Интерполяцией по энтропии на изобаре 1 бар определяем h₂ = 3328,2 кДж/кг. Тогда скорость истечения

.

Расхождение при определении скорости истечения с помощью диаграммы h,s и таблиц термодинамических свойств воды и водяного пара составляет 0,71 % в первом и 0,34 % во втором случае (точность расчетов по таблицам выше, чем по диаграмме h,s).

Задача 3

Перегретый пар с начальными параметрами р₁ = 14,0 МПа и t₁ = 450 °С вытекает в среду с давлением р_а = 2,2 МПа. Определить форму и размеры канала, обеспечивающего максимальное ускорение потока пара, действительную скорость истечения и размеры сопла, если скоростной коэффициент φ = 0,96, а расход пара т = 6,4 кг/с.

Решение

Рассчитываем отношение давлений β = р_а/р₁ = 2,2/14,0 = 0,1571. Поскольку β < β_к (0,1571 < 0,546), канал должен иметь как сужающуюся, так и расширяющуюся части, то есть для максимального ускорения потока надо использовать сопло Лаваля.

В соответствии с рассмотренным выше алгоритмом расчета адиабатного процесса истечения с помощью h,s диаграммы, определяем значения энтальпии пара в начальном и конечном состояниях процесса (на входе и выходе из сопла): h₁ = 3176 кДж/кг, h₂ = 2744 кДж/кг.

Действительная скорость истечения рассчитывается по формуле

.

Для расчета площади выходного сечения сопла f₂ определяем действительное значение энтальпии по формуле (3.9)

.

Тогда точка на изобаре р₂ = 2,2 МПа со значением энтальпии соответствует действительному состоянию пара на выходе из сопла. Определив по диаграмме h,s соответствующее значение удельного объема пара в этой точке = 0,091 м³/кг, рассчитываем значение площади выходного сечения сопла f₂ из уравнения сплошности

.

Скорость пара в минимальном сечении сопла сначала определим приближенным способом. Так как процесс истечения пара происходит преимущественно в области перегретого пара, принимаем значение β_к = 0,546 и вычисляем критическое давление истечения

.

Определив точку пересечения изобары р_к = 7,644 МПа с изоэнтропой, исходящей из точки 1, находим значения энтальпии в этой точке: h_к = 3016 кДж/кг. Тогда действительная скорость пара в минимальном сечении сопла

.

(значение скоростного коэффициента φ по длине сопла принимаем постоянным).

Далее рассчитываем действительное значение энтальпии в минимальном сечении (при давлении р_к)

.

На пересечении изобары р_к = idem и изоэнтальпы определяем действительное значение удельного объема в минимальном сечении сопла = 0,033 м³/кг. Тогда площадь этого сечения

.

Полагая, что расширяющаяся часть сопла имеет коническую форму с углом раствора γ = 10 °, на основании рассчитанных значений f₂ и f_min определяем диаметры минимального и выходного сечений d_min и d₂, а также длину l расширяющегося участка сопла

.

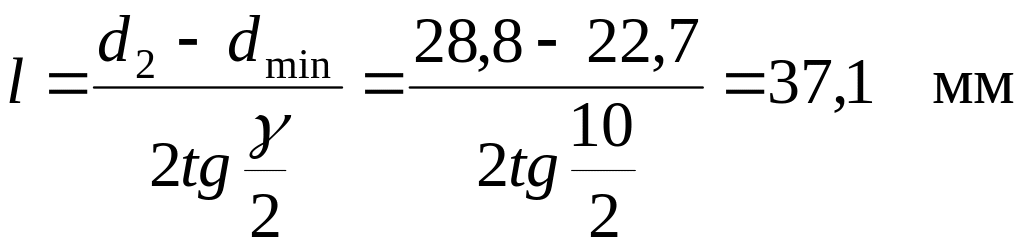Уточним выполненные расчеты с помощью таблиц термодинамических свойств воды и водяного пара [3]. С наибольшей погрешностью при использовании диаграммы h,s определяются значения удельного объема, поэтому начнем с уточнения этого параметра.

При давлении р_к и энтальпии пар перегрет, поэтому значение определяем по таблице ІІІ [3] методом двойной интерполяции: сначала интерполируем на крайних изобарах 76 и 78 бар, учитывая, что = 3029 кДж/кг, а затем по давлению при р_к = 76,44 бар. Уточненное значение = 0,03258 м³/кг.

Адиабатный процесс истечения оканчивается в области влажного пара при давлении р = 2,2 МПа. Зная, величину = 2778 кДж/кг из соотношения рассчитываем = 0,9887, а затем из формулы определяем значение = 0,08963 м³/кг.

На основании уточненных значений и рассчитываем площади сечений и длину расширяющейся части сопла по приведенным выше соотношениям

f_min = 384 мм²; f₂ = 643 мм²; d_min = 22,1 мм; d₂=28,6 мм; l = 37,1 мм.

Полученные значения также являются приближенными, поскольку основная часть расчетов выполнена с помощью диаграммы h,s, и к тому же при определении f_min использовано приближенное значение β_к.

Для точного определения размеров сопла необходимо рассчитать процесс течения по таблицам [3], определить значения w и v при промежуточных давлениях и рассчитать соответствующие значения f. Построив график зависимости f = F(p), определим значения f_min, d_min, f₂, d₂ и l.

Итак, в начальном состоянии (при р₁ = 140 бар и t₁ = 450 °С) значения энтальпии и энтропии по [3] (табл.III,стр.141) равны: h₁ = 3175,8 кДж/кг, s₁ = 6,1953 кДж/(кг·К). С целью повышения точности определения минимального значения зависимости f = F(p) задаёмся конечным давлением р_а=р₂ и рядом промежуточных значений: в окрестности найденного выше значения р_к используем все изобары, имеющиеся в табл. III, [3]. Учитывая условие s₁= idem, линейной интерполяцией на промежуточных изобарах p_i определяем соответствующие значения h_i и вычисляем разности h₁-h_i. Зная скоростной коэффициент φ, рассчитываем действительные значения h_i,д, а интерполяцией на тех же изобарах определяем значения удельных объемов v_i.

В тех случаях, когда действительное промежуточное состояние потока находится в области влажного пара, значения энтальпии и удельного объема определяем с помощью табл. ІІ [3]. Сначала рассчитываем степень сухости пара из аддитивной формулы при условии s_i = s₁, а затем вычисляем значения h_2i и h_2i,д. На основании h_2i,д рассчитываем действительную степень сухости и вычисляем v_2i,д. В том случае, если значение h_2i попадает в область влажного пара, а значение h_2i,д – в область перегретого пара, значение v_2i,д определяем интерполяцией на соответствующей изобаре по значению h_2i,д. Используя полученные значения h₁ – h_2i,д и v_2i,д, рассчитываем действительную скорость течения при данном давлении и соответствующие значения площадей поперечных сечений сопла . Результаты расчетов сводим в таблицу.

По приведенным в таблице данным четко просматривается значение f_min = 384,9 мм², что подтверждается построением зависимостей f = F(p) и w = W(p), из которых следует, что значения давления пара и скорости потока в минимальном сечении (7,83 МПа и 531,4 м/с) на 2,4 и 2,2 % отличаются от найденных выше (7,644 МПа и 543,0 м/с).

На основании уточненных значений f₂ и f_min получаем следующие размеры сопла: d₂ = 28,68 мм; d_min = 22,14 мм; l = 37,38 мм.

Кстати, расчет сопла с помощью диаграммы h,s при условии определения значений удельного объема пара по таблицам дает размеры сопла, вполне удовлетворительно согласующиеся с уточненными (рассчитанными только по таблицам).

р, МПа	h, кДж/кг	h1-h, кДж/кг	, кДж/кг	, м3/кг	, м/с	f, мм
10,0	3084,7	91,1	3091,8	0,02625	409,8	410,0
9,0	3057,5	118,3	3066,8	0,02857	466,9	391,6
8,4	3040,1	135,7	3050,7	0,03020	500,1	386,5
8,2	3034,0	141,8	3045,1	0,03079	511,2	385,5
8,0	3027,9	147,9	3039,5	0,03141	522,1	385,0
7,8	3021,6	154,2	3033,7	0,03206	533,1	384,9
7,6	3015,2	160,6	3027,8	0,03274	544,1	385,1
7,4	3008,7	167,1	3021,8	0,03346	555,0	385,8
7,2	3002,0	173,8	3015,6	0,03420	566,0	386,7
7,0	2995,2	180,6	3009,4	0,03499	576,9	388,2
6,0	2958,5	217,3	2975,5	0,03960	632,9	400,4
2,2	2746,8	429,0	2780,4	0,08975	889,2	646,0