Глава 6

ХАРАКТЕРИСТИКИ ТУРБИН И ТУРБОБУРОВ

§ 25. Характеристика турбины при постоянном расходе жидкости

П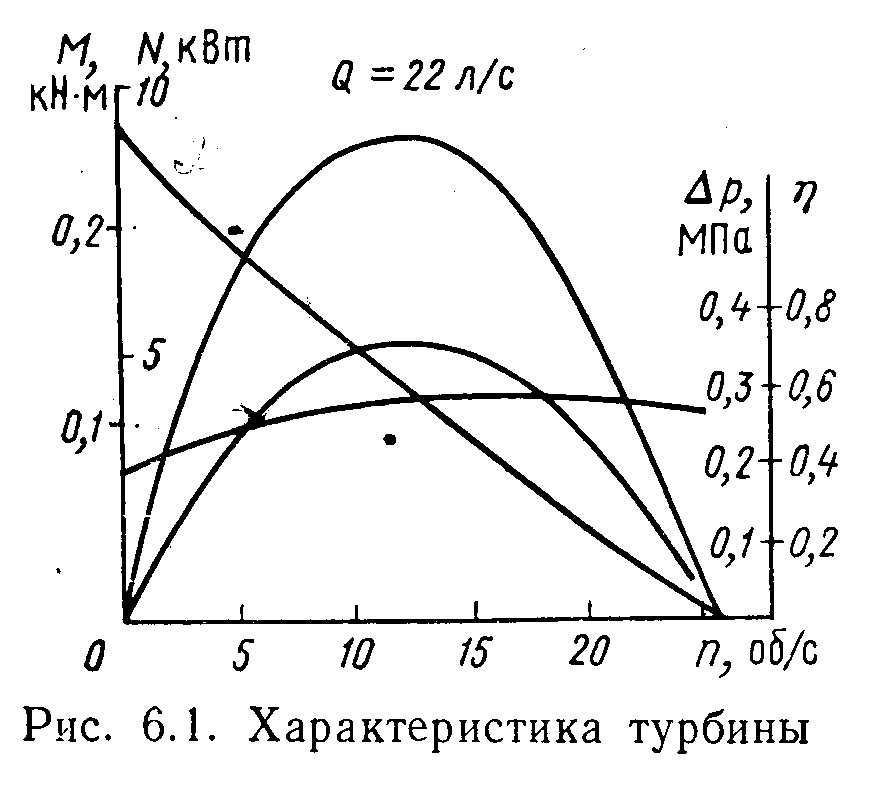 од характеристикой турбины турбобура понимается взаимосвязь между основными техническими показателями. Обычно она представлена графически кривыми зависимости момента М, перепада давления p_т, мощности N и к. п. д.  от частоты вращения вала n при постоянном значении расхода Q жидкости с определенными свойствами (плотность, вязкость и др.) (рис. 6.1).

Кривые n—М и n—p_т строят по результатам стендового испытания нескольких ступеней турбины при постоянном расходе воды для полного числа ступеней, составляющих турбину турбобура, и для данной плотности жидкости. При этом исходят из того, что М и p_т пропорциональны числу ступеней и плотности жидкости, а влиянием вязко-пластичных свойств промывочной жидкости на характеристику турбины пренебрегают.

Две другие кривые строят по первым двум, используя формулы

N=M; =N/p_тQ.

Если изменить шкалу по оси ординат, то линия перепада давления может служить также для определения гидравлической мощности, так как N_г=p_тQ, а Q — постоянная.

Линию моментаn—М (нагрузочную характеристику) приближенно можно построить теоретическим путем по размерам турбины и углам наклона лопастей, используя формулу Эйлера (5.2).

Из планов скоростей

c_1u=c_zctg₁; c_2u=u-c_zctg₂, так что M=Q[c_z(ctg₁ +ctg₂)-u]r_cp.

При холостом режиме М = 0 и, следовательно, u_max= c_z(ctg₁ +ctg₂).

u_max зависит только от расхода и поэтому относится к параметрам характеристики.

Формула момента выражает линейную зависимость:

M=Q(u_max-u)r_cp.

Мощностьтурбины

N= M=Q(u_max-u)u.

Это — уравнение квадратичной параболы, проходящей через нуль в точках с координатами u=0 и u=u_max. Середина интервала скоростей между 0 и u_max соответствует режиму максимальной мощности, называемому экстремальным. Максимальная мощность турбины

N_max=(1/4)Qu_max²

Из плана скоростей холостого режима (см. рис. 5.2, справа внизу) видно, что коэффициент циркуляции =(u_max-u_б)/u_б, откуда u_б=u_max/(1+). Следовательно, у низкоциркуляционных турбин (<1) безударному режиму соответствует точка, расположенная справа, а у высокоциркуляционных (>1) — слева от середины графика. Безударный режим нормальной турбины (=1) является также экстремальным.

Линия давления.

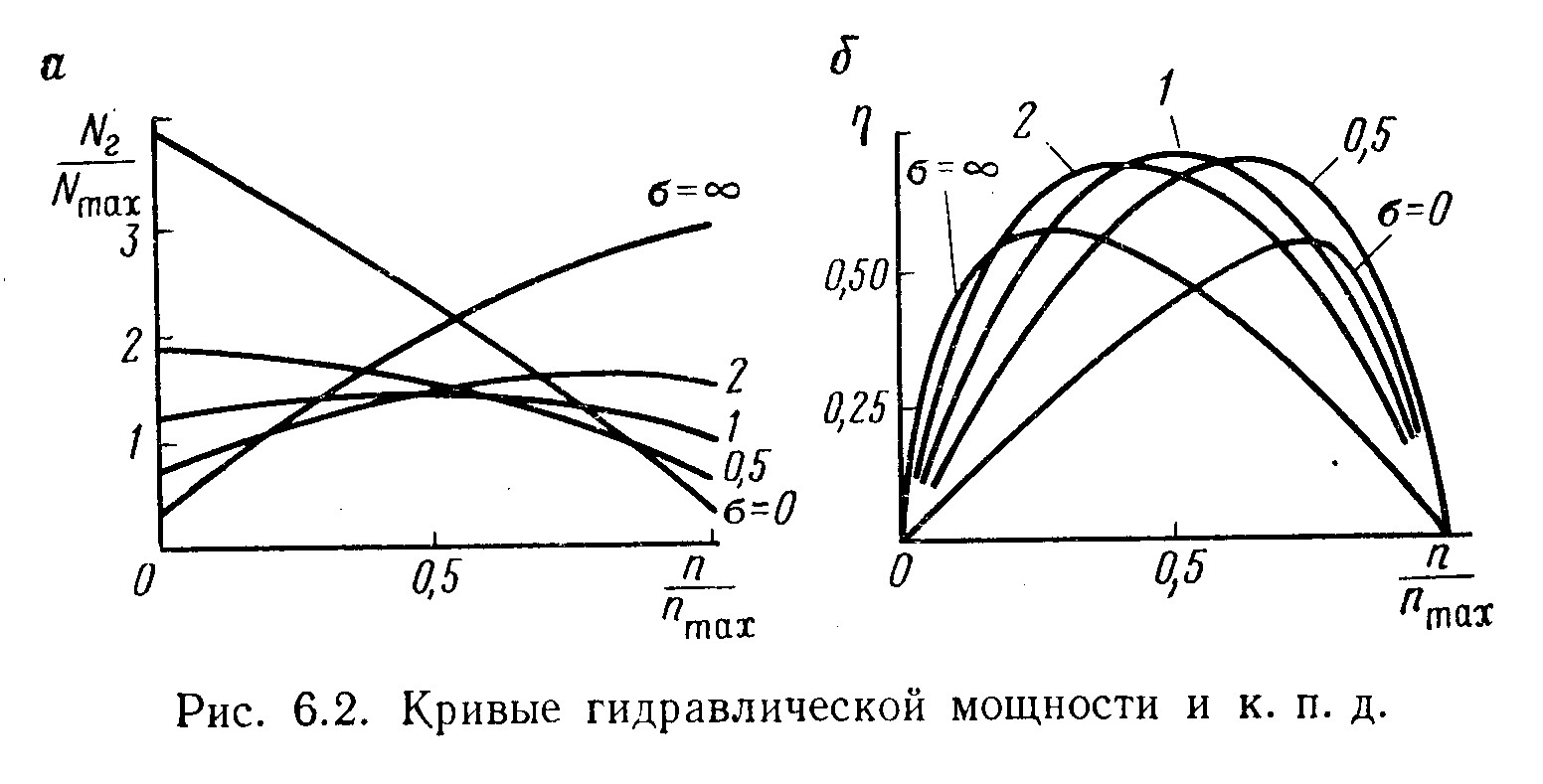
На рис. 6.2, а показаны кривые для турбин с различными коэффициентами циркуляции  при ; b₁ = 0,85; b₂ = 0,65. Поскольку при постоянном расходе жидкости N_гпропорциональна перепаду давления в турбине, то указанные кривые являются и линиями давления:

Для нормальной турбины линия давления почти симметрична относительно середины графика. Некоторая асимметрия вызвана увеличением вихревых потерь в левой части графика по сравнению с потерями в правой части (b₁>b₂).

Линия к. п. д. Турбины. Эту линию можно построить теоретическим путем, используя формулу (6.2):

(6.3)

Воспользуемся условием d/dn=0, считая, что вблизи максимума к. п. д. значения коэффициентов b₁ и b₂ можно заменить их средним значением b_cp=1/2(b₁+b₂).

Опуская преобразования, запишем полученное значение оптимальной частоты вращения вала , где Как видно, при заданном  положение максимума к. п. д. зависит от отношения двух показателей: и b_cp. Влияние коэффициента циркуляции на форму кривой к. п. д. показано на рис. 6.2, б. При построении кривых использованы указанные значения , b₁, b₂.

Точка, соответствующая оптимальному режиму, расположена между точками экстремального и безударного режимов. Так, для кривой при =0 (плоские лопасти) n_б=1 и , а для кривой при а и т. д. Чем меньше постоянные потери , тем ближе точка оптимального режима к точке безударного. В случае идеальной турбины, совершенной в гидравлическом отношении ( =0), обе точки совпадают. Если  = 1, то всегда n₀=n_б=n_э, т.е. оптимальный режим является безударным и экстремальным.

Из сравнения характеристик турбин, имеющих одинаковую частоту вращения n_max (см. рис. 6.2, б), можно сделать вывод, что нормальная турбина обладает наивысшим к. п. д., поскольку относительные потери для всех  приняты одинаковыми. Однако в действительности при умеренном уменьшении коэффициента циркуляции до некоторого значения <1 вследствие уменьшения кривизны межлопастных каналов потери в венцах снижаются, что и обеспечивает некоторое увеличение к. п. д.