3.3. Расчет цилиндрических зубчатых передач

Исходные данные при заданной схеме передачи (получены из кинема-тического расчета привода):

– вращающий момент на колесе, Нм;

– частота вращения колеса, об/мин;

– передаточное отношение;

– требуемый ресурс (время работы), ч;

вид передачи (прямозубая или косозубая);

циклограмма нагружения;

характер производства – единичный, мелкосерийный, крупносерийный.

Проектный расчет на контактную выносливость

В ходе проектного расчета закрытых прямо- и косозубых зубчатых передач устанавливают предварительные размеры передачи.

1. Выбирают материал и способ обработки (п. 3.2.1).

2. Рассчитывают допускаемые контактные напряжения и напряжения изгиба (п. 3.2.2).

3. Определяют коэффициент относительной ширины колес . Этот параметр выбирают в следующих пределах: для колес из улучшенных сталей при несимметричном расположении относительно опор принимают , из закаленных сталей при таком же расположении 0,25…0,315; для любых колес при симметричном расположении относительно опор 0,4.. 0,5; для шевронных колес 0,6..0,8; для передвижных шестерен коробок передач .

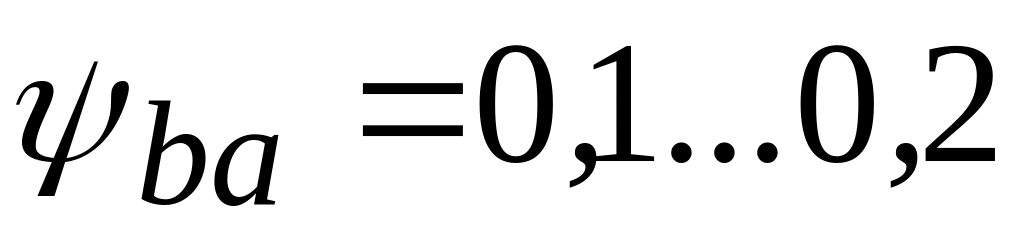4. Определяют межосевое расстояние передачи.

По ГОСТ 21354-87 сначала вычисляют ориентировочное значение межосевого расстояния, мм.

, (3.3.1)

где – расчетный коэффициент; для прямозубых передач , для косозубых и шевронных ; – передаточное число; – вращающий момент на колесе, Н∙м; – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактной линии. При проектном расчете принимают (меньшее значение при твердости материала колес , большее – при ), – допустимое контактное напряжение, МПа (п. 3.2.2).

Полученное значение округляют по (ГОСТ 2185-66*) до ближайшего числа из рядов, имея в виду, что значения первого ряда предпочтительнее:

1-й ряд – 40, 50, 63, 80, 100, 125, 160, 200, 250, 315, 400, 500, 630, 800;

2-й ряд – 140, 180, 225, 280, 355, 450, 560, 710, 900.

5. Принимают нормальный модуль для прямозубых передач (он же является окружным модулем ) в зависимости от : для нормализованных или улучшенных колес , для колес с закаленными зубьями . Выбранное значение модуля округляют до ближайшего стандартного (ГОСТ 9563-60**), имея в виду, что значения без скобок предпочтительнее: 1; 1,25; 1,5; (1,75); 2; (2,25); 2,5; (2,75); 3; (3,25); 3,5; (3,75); 4; (4,25); 4,5; 5; (5,5); 6; 6,5; (7); 8; (9); 10; (11); 12.

Для прямозубых передач с целью сохранения стандартного значения модуль необходимо назначать кратным этому значению.

6. Определяют числа зубьев шестерни и колеса:

для прямозубых передач

; ; ; (3.3.2)

для косозубых передач

, (3.3.3)

где – суммарное число зубьев шестерни и колеса; – угол наклона зубьев, град.

Предварительно принимают = 8…20°. Нижнее значение ограничено с целью обеспечения минимума двухпарного зацепления, верхнее – во избежание больших осевых сил. Для шевронных колес = 25…30° (40°).

Полученное значение округляют до ближайшего целого значения и уточняют угол зубьев

. (3.3.4)

В этом случае сохранится стандартное значение межосевого расстояния.

Для косозубых колес число зубьев шестерни при некорригированном зацеплении выбирают из условия

. (3.3.5)

7. Далее определяют остальные гео­метрические параметры.

• При некоррегированном зацепле­нии делительные диаметры, мм, соот­ветственно шестерни и колеса (рис. 3.3.1) с точностью до сотых долей вычисляют по формулам

, (3.3.6)

.

.

Рис. 3.3.1. Геометрические параметры цилиндрической зубчатой передачи

• Затем проверяют межосевое рассто­яние:

. (3.3.7)

• Ширина колеса, мм:

, (3.3.8)

где – рабочая ширина венца зубчатого колеса.

Для косозубых передач необходимо проверять условие

. (3.3.9)

Ширину шестерни принимают приблизительно на 5 мм больше шири­ны с целью компенсации возможных погрешностей сборки.

• Диаметры окружностей, мм, соот­ветственно вершин и впадин зубьев шестерни:

;

. (3.3.10)

• Диаметры окружностей, мм, соответ­ственно вершин и впадин зубьев колеса:

;

. (3.3.11)

После выполнения проектного расче­та, учитывая, что основным видом разру­шения закрытых зубчатых передач явля­ется усталостное выкрашивание (питтинг) поверхности зубьев вблизи полюс­ной линии, переходят к проверочному расчету на контактную выносливость.

Проверочный расчет на выносливость по контактным напряжениям

Согласно ГОСТ 21354-87 этот расчет выполняется по условию

. (3.3.12)

Контактное напряжение, МПа, без учета дополнительных нагрузок ( ):

, (3.3.13)

где – коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес, МПа: для стали МПа; – коэффи-циент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления; – коэффициент, учитывающий суммарную длину контактных линий; – окружная сила, Н: .

Коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления:

, (3.3.14)

где – угол зацепления, град.

При

. (3.3.15)

Коэффициент рекомендуется определять по формулам:

для прямозубых колес

, (3.3.16)

для косозубых колес

, (3.3.17)

где – коэффициент торцевого перекрытия зубьев, определяемый по выражению

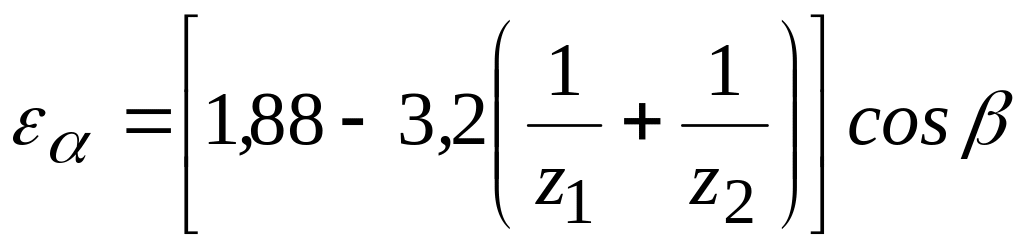. (3.3.18)

Коэффициент нагрузки в зоне контакта зубьев:

, (3.3.19)

где – коэффициент, учитывающий внешнюю динамическую нагрузку, , если в циклограмме учтены внешние нагрузки; в других случаях необ-ходимо использовать данные таблиц 3.3.1, 3.3.2, 3.3.3; – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий. Значение выбирают в зависимости от твердости поверхности зубьев, ширины колес и схемы передач (см. рис. 3.3.2); – коэффициент, учитывающий внутреннюю динамическую нагрузку; – коэффициент, учитывающий распределения нагрузки между зубьями (ГОСТ 21354-87): для прямозубых передач , для косозубых и шевронных значение определяют по графику (см. рис. 3.3.3).

Таблица 3.3.1

Коэффициент К_А внешней динамической нагрузки

при расчетах на усталостную прочность

Режим нагружения двигателя	Значение коэффициента КА при режиме нагружения ведомой машины
	равномерном	с малой неравно-мерностью	со средней неравно-мерностью	со значительной неравно-мерностью
Равномерный	1	1,25	1,5	1,75
С малой неравномерностью	1,1	1,35	1,6	1,85
Со средней неравномерностью	1,25	1,5	1,75	Свыше 2
Со значительной неравномерностью	1,5	1,75	2	Свыше 2,25
Примечание: 1. Табличные значения равны отношению эквивалентных нагрузок к номинальным и распространяются на передачи, работающие вне резонансной области. 2. При наличии в приводе гидравлических и упругих муфт, демпфирующих колебания, табличные значения коэффициента КА могут быть уменьшены на 20…30 % при условии, что КА ≥ 1. 3. Двигатели и машины, работающие в указанных здесь режимах, перечислены в таблицах 3.3.2, 3.3.3.

Таблица 3.3.2

Характерные режимы нагружения двигателей

Режим нагружения	Вид двигателя
Равномерный	Электродвигатель; паровые и газовые турбины при стабильных режимах эксплуатации и небольших пусковых моментах
С малой неравномерностью	Гидравлические двигатели, паровые и газовые турбины при больших часто возникающих пусковых моментах
Со средней неравномерностью	Многоцилиндровый двигатель внутреннего сгорания
Со значительной неравномерностью	Одноцилиндровый двигатель внутреннего сгорания

Таблица 3.3.3

Характерные режимы нагружения ведомых машин

Режим нагружения	Вид рабочей машины
Равномерный	Электрический генератор; равномерно работающие ленточные и пластинчатые конвейеры; легкие подъемники; упаковочные машины; вентиляторы; перемешивающие устройства и мешалки для веществ равномерной плотности; турбоком-прессоры; легкие центрифуги; механизмы с вращающимися деталями
С малой неравномерностью	Неравномерно работающие ленточные и пластинчатые транспортеры (для штучных грузов); шестеренные и ротационные насосы; главные приводы станков; тяжелые подъемники; механизмы кранов с вращающимися деталями; тяжелые центрифуги; перемешивающие устройства и мешалки для веществ переменой плотности; поршневые многоцилиндровые, гидравлические насосы; экструдеры; каландры
Со средней неравномерностью	Экструдеры; мешалки с прерывающимся процессом; легкие шаровые мельницы; деревообрабатывающие станки; одноцилиндровые поршневые насосы; подъемные машины
Со значительной неравномерностью	Экскаваторы, черпалки (приводы ковшей, цепных черпалок, грохотов); тяжелые шаровые мельницы; резиносмесители; дробилки; кузнечные машины; тяжелые дозировочные насосы; ротационные буровые машины; брикетные прессы

Рекомендуемые степени точности изготовления зубчатых передач в зависимости от их назначения и окружной скорости указаны в таблице 3.3.4.

Рис. 3.3.2. Графическое определение значений К _Fβ и К _Hβ: цифры на кривых соответствуют передачам на схемах; более точное определение К _Fβ и К _Hβ

по ГОСТ 21354-87.

Коэффициент , учитывающий внутреннюю динамическую нагрузку, при необходимости точного расчета рекомендуется определять по формуле

, (3.3.20)

где – удельная окружная динамическая сила, Н/мм, – расчетная удельная окружная сила в зоне наибольшей ее концентрации, Н/мм.

Удельная окружная динамическая сила, Н/мм:

, (3.3.21)

где – коэффициент, учитывающий влияние вида зубчатой передачи и моди-фикации профиля головок зубьев (табл. 3.3.5); – коэффициент, учитываю-щий влияние разности шагов зацепления зубьев шестерни и колеса (табл. 3.3.6); – окружная скорость, м/с; – межосевое расстояние, мм; и – передаточное число.

Таблица 3.3.4

Рекомендуемые степени точности изготовления зубчатых передач

Вид передачи	Степень точности изготовления передачи при окружной скорости ω, м/с
	до 5	5…8	8…12,5	свыше 12,5
Цилиндрическая: прямозубая косозубая	9 9	8 9	7 8	6 7
Коническая: прямозубая с круговыми зубьями	8 9	7 9	- 8	- 7

Таблица 3.3.5

Значение коэффициента

Твердость поверхностей зубьев по Виккерсу	Вид зубьев
HV1 ≤ 350 или HV2 > 350	Прямые без модификации головки Прямые с модификацией головки Косые	0,06 0,04 0,02
HV1 > 350 и HV2 >350	Прямые без модификации головки Прямые с модификацией головки Косые	0,14 0,10 0,04

Таблица 3.3.6

_{Значение коэффициента}

Модуль m, мм	при степени точности изготовления передачи по нормам плавности (ГОСТ 1643 – 81)
	5	6	7	8	9	10
До 3,55	2,8	3,8	4,7	5,6	7,3	10
Свыше 3,55	3,1	4,2	5,3	6,1	8,2	11
Свыше 10	3,7	4,8	6,4	7,3	10	13,5

Если значения , вычисленные по формуле (3.3.21), превышают предельные значения, указанные в таблице 3.3.7, то следует принимать предельные значения из таблицы.

Таблица 3.3.7

Предельные значения и , Н/мм

Модуль m, мм	, при степени точности изготовления передачи по нормам плавности (ГОСТ 1643 – 81)
	5	6	7	8	9	10
До 3,55	85	160	240	380	700	1200
Свыше 3,55	105	194	310	410	880	1500
Свыше 10	150	250	450	590	1050	1800

Расчетная удельная окружная сила в зоне ее наибольшей кон­цен­трации, Н/мм:

.

Для расчетов зубчатых передач объектов общего машиностроения с достаточной точностью можно использовать значения коэффициентов , указанные в таблице 3.3.8.

Таблица 3.3.8

_{Значения коэффициентов нагрузки KНυ и КFv}

Степень точности изготов-ления передачи	Твердость поверхностей зубьев	KНυ							КFv
		при окружной скорости v, м/с
		1	5	10	15	20	1	5		10	15	20
6	HВ1≤ 350 или HВ2> 350
	HВ1> 350 и HВ2> 350
7	HВ≤350 или HВ2> 350
	HВ1> 350 и HВ2> 350
8	HВ1≤ 350 или HВ2> 350
	HВ1> 350 и HВ2> 350
9	HВ1≤ 350 или HВ2> 350											-
	HВ1> 350 и HВ2> 350

Рис. 3.3.3. График для определения коэффициента для косозубых и шевронных передач, а также конических передач с круговыми зубьями (цифры соответствуют степени точности передачи)

Если нагрузка передачи по контактным напряжениям выше 10% или перегрузка более 5%, то необходимо скорректировать ширину колеса, межосевое расстояние или применить другой материал.

Проверочный расчет на контактную прочность при перегрузках

В этом случае при действии максимальной нагрузки :

. (3.3.22)

Наибольшее в течение заданного срока службы контактное напряжение определяют по формуле

, (3.3.23)

где – коэффициент нагрузки, определяемый при .

Допустимое предельное напряжение принимают в зависимости от способа химико-термической обработ­ки зубчатого колеса:

для зубчатых колес, подвергнутых нормализации, улучшению, объемной закалке:

; (3.3.24)

для зубьев, подвергнутых цемента­ции или контурной закалке:

; (3.3.25)

для азотированных зубьев:

. (3.3.26)

Проектный расчет на выносливость зубьев при изгибе

В процессе этого расчета определяют размеры закрытых зубчатых передач, у которых твердость колес НВ > 350, и открытых зубчатых передач.

Исходные данные для расчета: цик­лограмма нагружения; параметр или межосевое расстояние ; число зубьев шестерни ; угол наклона зуба ; коэффициент осевого перекрытия ( или ); материал и твердость рабочих поверхностей зубьев.

При предварительных расчетах параметр можно принимать по таблице 3.3.9.

Таблица 3.3.9

Рекомендуемые значения

Расположение колеса относительно опор	при твердости рабочих поверхностей зубьев
	НВ2 ≤ 350 или НВ1 ≤ 350 и НВ2 ≤ 350	НВ1 > 350, НВ2 > 350
Симметричное	0,8…1,4	0,4…0,9
Несимметричное	1,6…1,2	0,3…0,6
Консольное	0,3…0,4	0,2…0,25

Число зубьев шестерни рекоменду­ется выбирать в пределах

Расчетное значение модуля при за­данном параметре определяют по фор-муле

, (3.3.27)

где – расчетный коэффициент: для прямозубых передач = 14; для косозубых при > 1 и шевронных передач = 11,2; для косозубых при ≤ 1 передач = 12,5; – нагрузка на шестерню; – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактной линии. Его принимают в зави­симости от параметра по графику; – допустимое напряжение изгиба; – коэффициент, учитывающий форму зуба.

Коэффициент определяют по графику (рис. 3.3.4) в зависимости от числа зубьев эквивалентного колеса .

Для передач, выполнен­ных без смещения исходного контура, с достаточной степенью точности значе­ние можно выбрать из табл. 3.3.10.

Таблица 3.3.10

для передач, выполнен­ных без смещения исходного контура

	16	17	20	25	30	40	50	60	80	100
	4,47	4,28	4,08	3,9	3,8	3,7	3,65	3,62	3,6	3,6

Рис. 3.3.4. График для определения коэффициента

в зависимости от эквивалентного числа зубьев

Силы, действующие в зацеплении передач

В прямозубой передаче в зоне зацепле­ния действует нормальная сила , ко­торая направлена по линии зацепления NN. Эту силу раскладывают на составля­ющие: окружную силу и радиальную . При заданном моменте , .

Для косозубой передачи составляющие нормальной силы (см. рис. 3.3.5) – ок­ружная сила , осевая и радиальная .

В шевронной передаче осевые силы взаимно уравновешива­ются и не передаются на валы и опоры.

Рис.3.3.5. Силы, действующие в зацеплении передач

Проверочный расчет зубьев на вынос­ливость при изгибе

Для предотвращения усталостного излома шестерни и колеса должно выполняться условие

, (3.3.28)

где – расчетное местное напряжение изгиба в опасном сечении; – допустимое напряжение.

Расчетное местное напряжение при изгибе определяют по формуле:

. (3.3.29)

Коэффициент нагрузки при изгибе:

. (3.3.30)

Коэффициент формы зуба выбирают в зависимости от числа зубьев эквивалентного колеса. Коэффициент , учитывающий распределение нагрузки по длине контактных линий при расчетах по напряжениям изгиба, определяют по графику (см. рис. 3.3.2) в зависимости от параметра , твердости поверхностей зубьев и места установки колес относительно опор.

Коэффициент , учитывающий динамическую нагрузку, можно определить по таблице 3.3.8 или формуле

. (3.3.31)

Удельную окружную динамическую силу при изгибе принимают для дальнейших расчетов по табли­це 3.3.7 или рассчитывают по выражению

, (3.3.32)

где – коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зубьев: для косозубых и шевронных передач = 0,06; для прямозубых передач с модификацией головки = 0,11; для прямозубых передач без модификации головки = 0,16; – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса (см. табл. 3.3.6); – окружная скорость, м/с.

Удельную расчетную окружную силу при расчете на изгибную прочность определяют по формуле

. (3.3.33)

Коэффициент учитывает распределение нагрузки между зубьями. Для расчета на выносливость при изгибе прямозубых передач можно принимать . Для косозубых и шевронных передач значения выбирают в зависимости от степени точности изготовления передачи:

Степень точности 6 7 8 9

0,72 0,81 0,91 1

При необходимости более точного расчета следует воспользоваться ре­комендациями ГОСТ 21354 – 87.

Коэффициент, учитывающий на­клон зуба:

, (3.3.34)

где – коэффициент осевого перекрытия. Желательно проектировать передачу так, чтобы был бы близок или равен целому числу.

Коэффициент, учитывающий перекрытие зубьев в прямозубых передачах, , в косозубых передачах – (при ) или (при ≥1).

Проверочный расчет на прочность по напряжениям изгиба при перегрузках

Прочность зубьев, необходимую для предотвращения остаточных деформаций, хрупкого излома или образования первичных трещин в поверхностном слое, определяют из условия

, (3.3.35)

т.е. сопоставляя расчетное и допустимое напряжения изгиба в опасном сечении при максимальной нагрузке.

Расчетное напряжение изгиба в опасном сечении

, (3.3.36)

где – максимальная нагрузка; – рабочая нагрузка.

Ориентировочно можно принимать при НВ < 350 и при НВ > 350 (здесь – предел текучести материала).