§ 3. Инвариантность относительно преобразования X  g(X)

Если выражение не меняется при замене x на некоторое выражение , то при решении уравнений (неравенств и т.д.) используют следующее утверждение.

Утверждение 5. Если выражение f(x) инвариантно относительно преобразования x  g(x) и уравнение f(x) = 0 имеет корень x₀, то и число g(x₀) также корень этого уравнения.

Пример 3.1. При каких значениях параметра a уравнение

имеет единственное решение? Определите это решение.

Решение.

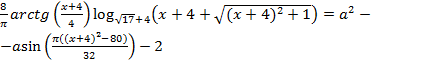
Пусть , тогда

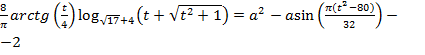
(1)

Убедимся, что в левой и правой частях уравнения находятся функции четные относительно переменно . 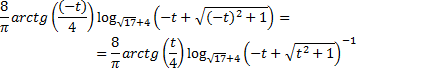Заметим, что

Значит

.

Таким образом, уравнение (1) будет инвариантно относительно замены на , а единственным его решением будет .

Подставим . , ,

Теперь проверим полученные значения параметра a.

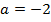1. Пусть , тогда

, , .

Несложно убедиться, что, кроме , корнем данного уравнения является .

Значит, значение не удовлетворяет условию задания.

2. Пусть ;

, .

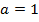Оценим левую и правую части уравнения: При

При и

Таким образом, левая часть уравнения при положительна и обращается в ноль только при .

Выражение всегда принимает неположительные значения.

Геометрическая интерпретация уравнения выглядит так:

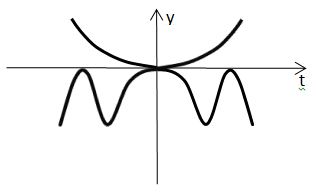
Значит, — единственное решение уравнения (1). А — единственное решение исходного уравнения. Ответ: .

Пример 3.2. При каких значениях параметра a уравнение имеет ровно 3 различных решения?

Решение.

Заметим, что уравнение инвариантно относительно замены . Несложно убедиться, что

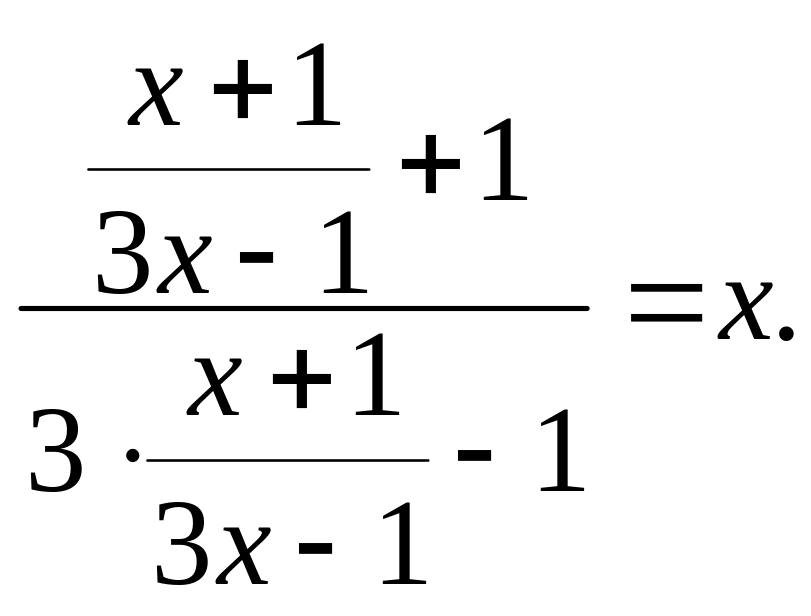
Поэтому, если — корень уравнения, то и — тоже корень.

Так как уравнение должно иметь нечетное число решений, в частности 3, то это возможно только в случае, если Тогда и .

При x = 1 получим a = 2, при получим .

Решим исходное уравнение для каждого из найденных значений параметра.

1) Пусть a = 2, тогда уравнение примет вид:

. Решая его, находим три корня: 1, , .

2) Пусть a = . В этом случае — единственное решение уравнения , что не удовлетворяет условию.

Ответ: a = 2.

§ 4. Задачи для самостоятельного решения

1. Найти все значения параметра а, при каждом из которых система уравнений имеет единственное решение?

2. Найти все значения параметра а, при каждом из которых система уравнений имеет два решения?

3. Найти все значения параметра a, при каждом из которых система уравнений имеет два решения?

4. При каких значениях параметра a система неравенств

имеет единственное решение?

5. При каких значениях параметра a уравнение имеет единственное решение?

6. При каких значениях параметр

имеет ровно четыре различных решения?

7. При каких значениях параметра a уравнение

(|x| – 3)² + 9||x| – 3| – (a + 6) = 0 имеет 3 решения? Найдите их.

8. При каких значениях параметров а и b система

имеет единственное значение?

9. При каких значениях параметра а уравнение

имеет на полуинтервале (–1; 1] ровно три корня?

10. При каких значениях параметра а система

имеет единственное решение?

11. При каких значениях параметра а уравнение

имеет единственное решение?

12. При каких значениях параметров а и b система

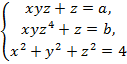
имеет единственное решение?

Ответы

1. .

2.

3. .

4. .

5. .

6. .

7.

8. .

9. .

10. . Указание. Сделать замену , и воспользоваться симметрией относительно перестановки переменных u и v.

11. — иррациональное.

12. . Указание. Воспользоваться симметрией относительно знака переменных x и y.