Муниципальное бюджетное общеобразовательное учреждение лицей при Томском политехническом университете

Применение инвариантности математических объектов при решении задач с параметрами

Томск 2012

Киреенко С.Г., Бабеева М.В., Баев А.Ю., Воткина Д.Е., Кобзев М.Г., Ляхович М.С., Степуро Е.К., Шендеров В.Ю., Шибанов М.Г. Применение инвариантности математических объектов при решении задач с параметрами: Учебное пособие. – Томск: Лицей при ТПУ, 2012. – 30 с.

Настоящее пособие предназначено для учащихся и преподавателей общеобразовательных учреждений. Пособие содержит основные теоретические сведения по применению инвариантности математических объектов, большое количество задач с разобранными решениями, а также задания для самостоятельного решения.

© Лицей при ТПУ, 2012

Оглавление

Введение 4

§ 1. Симметрия относительно знака переменных 5

§ 2. Симметрия относительно перестановки переменных 18

§ 3. Инвариантность преобразования x  g(x) 24

§ 4. Задачи для самостоятельного решения 29

Ответы . 31

Введение

Инвариант или инвариантность — термин, обозначающий нечто неизменяемое. Инвариант в математике — это свойство некоторого класса (множества) математических объектов оставаться неизменными при преобразованиях определенного типа.

В данном пособии речь пойдет о задачах, в которых условия не изменяются либо при замене знака одной или нескольких переменных на противоположный (симметрия относительно знака), либо при перестановке нескольких переменных (симметрия относительно перестановки переменных), либо при замене переменной на некоторое выражение с переменной.

При решении задач указанного вида используется следующий алгоритм:

1. выполняется проверка на инвариантность;

2. из проверки выполнения необходимых условий находятся допустимые значения параметра (при «симметрии относительно знака» переменной подставляется ее нулевое значение; при «симметрии относительно перестановки» переменных все переменные обозначают одной буквой);

3. проверятся достаточность условий, т.е. для найденных допустимых значений параметра выполняется проверка того, что при полученных значениях параметра уравнение (неравенство, система и т.д.) действительно имеет требуемое число решений.

Замечание. Последний этап заключается либо в доказательстве существования требуемого числа решений, либо в его опровержении.

Приведенный алгоритм является общим и для решения уравнений и неравенств, а также систем уравнений и неравенств с одним или несколькими параметрами.

§ 1. Симметрия относительно знака переменных

Выражения, инвариантные относительно преобразования или , называют симметричными относительно знака переменной, или переменной y. При решении уравнений (неравенств, систем уравнений или неравенств) используют следующие утверждения.

Утверждение 1. Если выражение f(x) инвариантно относительно преобразования x(-x) и уравнение f(x)=0 имеет корень x₀ , то число -x₀ также корень этого уравнения.

Утверждение 2. Если выражение f(x, y) инвариантно относительно преобразования x(-x) и уравнение f(x, y)=0 имеет решение (x₀, y₀), то и пара чисел (-x₀, y₀) также решение этого уравнения.

Утверждение 3. Если выражение f(x, y) инвариантно относительно преобразования y(-y) и уравнение f(x, y)=0 имеет решение (x₀, y₀), то и пара чисел (x₀, -y₀) также решение этого уравнения.

Для четных функций выражение симметрично относительно знака переменной x. Как известно, график четной функции симметричен относительно прямой . Если для выражения выполняется равенство , т. е. график функции симметричен относительно прямой , то удобнее сделатьзамену , чтобы рассматривать четную функцию f(t).

При исследовании на «симметрию относительно знака» в выражении для пары проверяются подстановкой в него пары . Если при подстановке пар и выражение не меняется, то говорят, что наблюдается «симметрия относительно знака» переменной ; для пар и – «симметрия относительно знака» переменной y; для пар и  — «симметрия относительно знаков» обеих переменных.

Пример 1.1. Найдите все значения параметра a, при каждом из которых система

имеет единственное решение.

Решение.

Так как функции, входящие в систему четные относительно переменной х, то если пара (x₀; y₀) является решением системы, то и пара (–x₀; y₀) — тоже решение. Следовательно, единственное решение системы имеет вид: (0; с).

Пусть x = 0, тогда

Рассмотрим 2 случая: y = 1 и y = –1.

1)

Пусть a = 1,2.

Из второго уравнения системы следует, что

Преобразуем первое уравнение системы:

Так как (с учетом условий (*)), то полученное уравнение равносильно системе

Вторая система совокупности не имеет решений (смотри условие ). Таким образом, при a = 1,2 исходная система имеет единственное решение (0; 1).

2)

Пусть a = 4.

Нетрудно убедиться, что данной системе удовлетворяют пары (0; –1), (1; 0) и (–1; 0).

В этом случае система будет иметь более одного решения.

Ответ: a = 1,2.

Пример 1.2. Найдите все значения параметра a, при каждом из которых система уравнений

имеет единственное решение.

Решение.

Данная система симметрична относительно замены x на –x. Поэтому единственным ее решением может быть решение вида (0; с).

Пусть x = 0, тогда

Рассмотрим отдельно случаи, когда a = 0 и a = 4 и убедимся в том, что пара вида (0; с) действительно является единственным решением.

1) Пусть a = 0, тогда

Решениями этой системы являются три пары чисел (2; 0), (–2; 0), (0; –2), что противоречит условию задачи.

2) Пусть a = 4, тогда

Из первого уравнения системы следует, что , а из второго, что . Следовательно, система может иметь решения, только если .

Имеем,

При a = 4 система имеет единственное решение (0; 2).

Ответ: а = 4.

Пример 1.3. Найдите все значения параметра , при которых имеет единственное решение система уравнений

Решение.

Система уравнений инвариантна относительно замены x на ( . Следовательно, если – решения системы, то пара также является решением этой системы. Система может иметь единственное решение только при x=0.

Пусть х = 0. Система примет вид

Проверим, что система не имеет других пар решений при , кроме (0; 1).

.

Уравнение имеет бесконечное количество решений.

Проверим, что система не имеет других пар решений при ,кроме .

Оценим левую и правую части первого уравнения получившейся системы.

;

Равенство выполняется только в случае, если обе его части принимают значение 2.

(0; 1) — единственная пара решений.

Ответ:

Пример 1.4. При каких значениях параметра а система

имеет единственное решение?

Решение.

Система инвариантна относительно одновременной замены знака обеих переменных;

Следовательно, если — решения системы, то пара также является решением этой системы. Тогда единственным решением системы может быть пара .

Подставим .

Проверим, что при других решений, кроме (0; 0), нет.

Т.к. и , то единственным решением первого уравнения системы является (0; 0).

Ответ: .

Пример 1.5. Найти значения параметра а, при котором уравнение

²

имеет 7 действительных корней, и найти эти корни.

Решение.

Уравнение инвариантно относительно смены знака переменной. Следовательно, если . Тогда, чтобы уравнение имело нечетное количество корней, в нашем случае 7, одним из решений должно быть х = 0.

Подставим х = 0.

² ,

.

Теперь найдем корни при

²

Пусть = t, тогда

² ,

t=1, t=4.

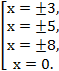
Итого 7 корней.

Ответ: , .

Пример 1.6. Определить значения параметра , при которых уравнение

имеет ровно 7 действительных корней, и найти эти корни.

Решение.

Уравнение инвариантно относительно замены на

Следовательно, если ₀ — решение данного уравнения, то (- ₀) — тоже решение.

Пусть (тогда уравнение должно иметь нечетное количество решений).

25 – 36+ a = 0.

a = 10.

Пусть .

Подставим a = 10 и найдем корни.

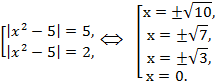
Итого 7 корней.

Ответ:

Пример 1.7. Найдите значения параметра a, при которых уравнение

имеет единственное решение.

Решение.

Пусть ,

+ 4α – 9 = 0; + 4α – 9 = 0; (2) Уравнение симметрично относительно замены t на (–t). Поэтому, если — решение, то и (- ) тоже решение. Следовательно, единственным решением будет . С помощью данного условия найдём необходимые значения .

,

Проверим, что при найденном , — единственный корень. 1) Пусть = 0 t = 0 – единственный корень уравнения(2), а значит, 2) Пусть =

Пусть , тогда

Решая данное уравнение графически, получаем:

А значит при уравнение (2) будет иметь более одного решения. Следовательно, уравнение (1) тоже будет иметь более одного решения и не подходит. 3)

; Пусть , тогда ;

Оценивая левую и правую части, мы получаем, что функция в левой части принимает значения [0; +∞), а функция в правой части — [–32; 0].

Получаем систему, равносильную исходному уравнению:

Решая данную систему, находим, что . 2πt = 0, а значит, — единственный корень. Соответственно, уравнение(1) имеет 1 решение.

Ответ: ;

Пример 1.8. Найдите все значения параметра , при которых система уравнений

имеет только одно решение.

Решение.

Система инвариантна относительно замены на . Тогда единственным решением системы может быть пара

Пусть .

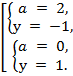
При найденных значениях ( ) исходная система имеет решение (0; ). Проверим, что это решение единственное.

1) Пусть .

Из второго уравнения системы следует, что . Тогда левая часть первого уравнения неположительная, а правая — неотрицательная. Следовательно, первое уравнение будет равносильно системе

Тогда единственным решением данной совокупности является пара . Вторая система не имеет решений в силу условия

2) Пусть

Можно убедиться, что кроме пары , решениями также являются . Значит, при система имеет более одного решения.

Ответ:

Пример 1.9. Найдите все значения параметра a, при которых неравенство

имеет единственное решение.

Решение.

Неравенство инвариантно относительно замены знака переменной и, следовательно, имеет единственное решение при 0.

Пусть .

.

При исходное неравенство содержит среди решений , найдем , при которых — единственный корень.

;

умножим обе части неравенства на ( ).

,

,

,

Т.к. , равенство равносильно системе уравнений единственным решением которой является .

2) .

Можно заметить, что в левой части неравенства при подстановке любого получается число, не превосходящее (–5), а в правой части при данных значениях параметра получается положительное число. , что не удовлетворяет условию задания.

Ответ: