30. Модель свободных электронов. Образование запрещенной зоны в сплошном энергетическом спектре свободных электронов под влиянием кристаллической решетки.

Подобно энергетическим уровням в изолированных атомах, энергетические зоны могут быть полностью заполненными, частично заполненными и свободными. Внутренние оболочки в изолированных атомах заполнены, поэтому соответствующие им зоны также оказываются заполненными. Самую верхнюю из заполненных зон называют валентной зоной. Эта зона соответствует энергетическим уровням электронов внешней оболочки в изолированных атомах. Ближайшую к ней свободную, незаполненную зону называют зоной проводимости. Между ними расположена запрещенная зона. Заполнение зоны проводимости начинается, когда электроны в валентной зоне получают дополнительную энергию, достаточную для преодоления энергетического барьера, равного ширине запрещенной зоны.

Отсутствие каких-либо уровней энергии в запрещенной зоне характерно только для совершенных кристаллов. Любые нарушения идеальности периодического поля в кристалле влекут за собой нарушения идеальности зонной структуры. В реальном кристалле всегда имеются дефекты кристаллической решетки. Если количество дефектов в кристалле невелико, то они будут находиться на значительных расстояниях друг от друга, локализованы. Поэтому изменяться будет энергетическое состояние только тех электронов, которые находятся в области дефекта, что приведет к образованию локальных энергетических состояний, накладывающихся на идеальную зонную структуру. Число таких состояний либо равно числу дефектов, либо превышает его, если с дефектом связано несколько таких состояний. Расположение локальных состояний ограничено областью вблизи дефекта. Электроны, находящиеся на этих энергетических уровнях, оказываются связанными с дефектами и поэтому не могут участвовать в электропроводности. Т. е. уровни дефектов, на которых они расположены, располагаются в запрещенной зоне кристалла.

С ростом температуры возрастает амплитуда тепловых колебаний атомов, увеличивается степень их взаимодействия и степень расщепления энергетических уровней. Поэтому разрешенные зоны становятся шире, а запрещенные, соответственно, уже. При изменении межатомных расстояний в зависимости от характера расщепления уровней ширина запрещенной зоны может как увеличиваться, так и уменьшаться. Это происходит, например, под действием давления на кристалл.

Зонная теория позволяет сформулировать критерий, который дает возможность разделить твердые вещества на два класса — металлы и полупроводники (диэлектрики). Зонная теория первоначально была разработана для кристаллических твердых тел, однако в последние годы ее представления стали распространяться и на аморфные вещества.

 Модель свободных электронов. Исходная модель металла

По современным представлениям металл можно рассматривать как совокупность системы большого числа N положительно заряженных колеблющихся ионов, образующих квазипериодическую пространственную структуру (кристаллическую решетку), и системы относительно свободных коллективизированных валентных электронов, не локализованных вблизи отдельных ионов, а перемещающихся по всему кристаллу. Отличие одного металла от другого связано с разной валентностью z атомов, особенностями их электронной структуры, а также с симметрией кристаллической решетки.

Т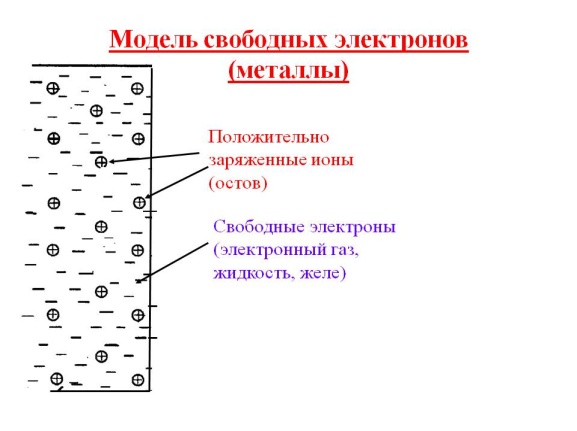 еоретическое описание металла в рамках такой модели приводит к квантовомеханической задаче о системе (N+zN) взаимодействующих между собой частиц. Строгое решение такой задачи в настоящее время невозможно.

Качественное представление о характере поведения электронов, их энергетическом спектре можно получить на основании следующих приближений.

Адиабатическое приближение.

Массы ионов, образующих кристаллическую решетку, и массы электронов, а, следовательно, и скорости их движения, сильно различаются (скорости - приблизительно на два-три порядка). Поэтому можно, считать, что, во-первых, движение электронов не зависит от движения ионов и, во-вторых, ионы в узлах решетки неподвижны и образуют строго периодическую кристаллическую решетку. Такое приближение называют адиабатическим или приближением Борна-Оппенгеймера.

Одноэлектронное приближение.

Взаимодействие электронов друг с другом можно заменить взаимодействием каждого электрона с усредненным полем всех остальных электронов. Это поле определяет не только движение данного электрона, но и само зависит от его движения, то есть является самосогласованным полем. Введение самосогласованного поля позволяет рассматривать электроны в кристалле как почти не взаимодействующие частицы. Полная энергия при этом равна сумме энергий отдельных электронов. Таким образом, самосогласованное поле позволяет задачу многих частиц свести к задаче для одного электрона (одноэлектронное приближение).

При этом электрон не является совсем свободным, так как находится в потенциальном поле всех ионов решетки и самосогласованном поле других электронов.