15.Волновые свойства микрочастиц. Задание состояния микрочастиц. Волновая функция, ее смысл и свойства Корпускулярные и волновые свойства частиц. Принцип неопределенности

    В 1900 г. была опубликована работа М. Планка, посвященная проблеме теплового излучения тел. М. Планк моделировал вещество как совокупность гармонических осцилляторов различной частоты. Предположив, что излучение происходит не непрерывно, а порциями - квантами, он получил формулу для распределения энергии по спектру теплового излучения, которая хорошо согласовывалась с опытными данными где h - постоянная Планка, k - постоянная Больцмана, T - температура, ν - частота излучения. Так, впервые в физике появилась новая фундаментальная константа - постоянная Планка. Гипотеза Планка о квантовой природе теплового излучения противоречит основам классической физики и показала границы ее применимости.  Через пять лет А. Эйнштейн, обобщив идею М. Планка, показал, что квантованность является общим свойством электромагнитного излучения. Согласно Эйнштейну электромагнитное излучение состоит из квантов, названных позднее фотонами. Каждый фотон имеет определенную энергию и импульс:E = hν,  = (h/λ) ,где λ и ν - длина волны и частота фотона, - единичный вектор в направлении распространения волны.   Представления о квантованности электромагнитного излучения позволили объяснить закономерности фотоэффекта, исследованные экспериментально Г. Герцем и А. Столетовым. На основе квантовой теории А. Комптоном в 1922 году было объяснено явление упругого рассеяния электромагнитного излучения на свободных электронах, сопровождающееся увеличением длины волны света. Открытие двойственной природы электромагнитного излучения - корпускулярно-волнового дуализма оказало значительное влияние на развитие квантовой физики, объяснение природы материи.

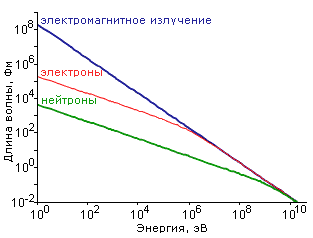Зависимость длины волны от энергии для различных частиц

В 1924 г. Луи де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Согласно этой гипотезе не только фотоны, но и любые другие частицы материи наряду с корпускулярными обладают также и волновыми свойствами. Соотношения, связывающие корпускулярные и волновые свойства частиц, те же, что были установлены ранее для фотоновE = h = ω, = , |p| = h/λ / ,где h = 2π , ω = 2πν, = 2π - длина волны, которую можно сопоставить с частицей. Волновой вектор ориентирован по направлению движения частицы. Прямыми опытами, подтверждающими идею корпускулярно-волнового дуализма частиц, были опыты, выполненные в 1927 году К. Дэвиссоном и Л. Джермером по дифракции электронов на монокристалле никеля. Позднее наблюдалась дифракция и других микрочастиц. Метод дифракции частиц в настоящее время широко используется в изучении строения и свойств вещества.     Экспериментальное подтверждение идеи корпускулярно-волнового дуализма привело к пересмотру привычных представлений о движении частиц и способа описания частиц. Для классических материальных точек характерно движение по определенным траекториям, так, что их координаты и импульсы в любой момент времени точно известны. Для квантовых частиц это утверждение неприемлемо, так как для квантовой частицы импульс частицы связан с ее длиной волны, а говорить о длине волны в данной точке пространства бессмысленно. Поэтому для квантовой частицы нельзя одновременно точно определить значения ее координат и импульса. Если частица занимает точно определенное положение в пространстве, то ее импульс полностью неопределен и наоборот, частица с определенным импульсом имеет полностью неопределенную координату. Неопределенность в значении координаты частицы Δx и неопределенность в значении компоненты импульса частицы Δp_x связаны соотношением неопределенности, установленным В. Гейзенбергом в 1927 году Δx·Δp_x .Из принципа неопределенности следует, что в области квантовых явлений неправомерна постановка некоторых вопросов, вполне естественных для классической физики. Так, например, не имеет смысла говорить о движении частицы по определенной траектории. Необходим принципиально новый подход к описанию физических систем. Не все физические величины, характеризующие систему, могут быть измерены одновременно. В частности, если время жизни некоторого состояния равно Δt, то неопределенность величины энергии этого состояния ΔE не может быть меньше ΔE/ , т.е.ΔE·Δt .

Классическая физика	Квантовая физика
1. Описание состояния
(x,y,z,px,py,pz)	(x,y,z)
2. Изменение состояния во времени
= H/ p,  = - H/ t,
3. Измерения
x, y, z, px, py, pz	х px ~ y py ~ z pz ~
4. Детерминизм. Статистическая теория
Динамическое (не статистическое) описание	| (x,y,z)|2
5. Гамильтониан
H = p2/2m + U(r)	= 2/2m + U(r)

    Состояние классической частицы в любой момент времени описывается заданием ее координат и импульсов (x,y,z,p_x,p_y,p_z). Зная эти величины в момент времени t, можно определить эволюцию системы под действием известных сил во все последующие моменты времени. Координаты и импульсы частиц сами являются непосредственно на опыте измеряемыми величинами. В квантовой физике состояние системы описывается волновой функцией (x,y,z). Т.к. для квантовой частицы нельзя одновременно точно определить значения ее координат и импульса и не имеет смысла говорить о движении частицы по определенной траектории, можно определить только вероятность нахождения частицы в данной точке в данный момент времени, которая связана с волновой функцией - * .   Изменение состояния классической частицы во времени описывается уравнениями Гамильтона = H/ p,  = - H/ t,где H - функция Гамильтона H = p²/2m + U(r), где U(r) - потенциал поля, в котором движется частица.В квантовой физике изменение состояния частицы описывается уравнением Шредингера где - оператор Гамильтона - аналог классической функции Гамильтона, в которой p и r заменены на операторы импульса и координаты .

px
x = x
= 2/2m + U(r)

В классической физике движение частицы в принципе с любой степенью точности определяется заданием начальных условий. В квантовой физике описание состояния имеет вероятностный характер. Вероятность W нахождения частицы в точке (x,y,z) определяется квадратом модуля волновой функции WdV = | (x,y,z)|²dV.    Измеряемые величины в квантовой физике являются статистическими средними, определяемыми соответствующими операторами Например средние значения координаты и импульса в состоянии, описываемом волновой функцией (x,y,z) даются соотношениями

16. Эволюционное уравнение Шредингера. Квантовый оператор энергии. Уравне́ние Шрёдингера — уравнение, описывающее изменение в пространстве (в общем случае, в конфигурационном пространстве) и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах

Уравнение Шрёдингера предназначено для частиц без спина, движущихся со скоростями много меньшими скорости света. В случае быстрых частиц и частиц со спином используются его обобщения (уравнение Клейна — Гордона, уравнение Паули, уравнение Дирака и др.) Наиболее общая форма уравнения Шрёдингера — это форма, включающая зависимость от времени

Общий случай

Пусть волновая функция задана в n-мерном конфигурационном пространстве, тогда в каждой точке с координатами , в определенный момент времени t она будет иметь вид . В таком случае уравнение Шрёдингера запишется в виде:

h— постоянная Планка; m— масса частицы, Ep — внешняя по отношению к частице потенциальная энергия в точке в момент времени t , — оператор Лапласа (или лапласиан), эквивалентен квадрату оператора набла и в n-мерной системе координат имеет вид:

Случай трёхмерного пространства

В трёхмерном случае неизвестные являются функциями трех координат и в декартовой системе координат заменяется выражением

тогда уравнение Шрёдингера примет вид:

Стационарное уравнение Шрёдингера

Форма уравнения Шрёдингера показывает, что относительно времени его решение должно быть простым, поскольку время входит в это уравнение лишь через первую производную в правой части. Действительно, частное решение для специального случая, когда не является функцией времени, можно записать в виде:

Квантовые операторы

Квантовые операторы − символические изображения математических операций преобразования величин в квантовой теории. В квантовой механике постулируется, что каждой физической величине, описываемой в классической механике функцией

F(x,y,z,px,py,pz) координат и импульсов, ставится в соответствие линейный операто ( , , ,) действующий на волновую функцию ψ(x,y,z,t). Под оператором понимается правило, по которому одной функции ψ(x,y,z,t) переменныx x, y, z, t сопоставляется другая функция χ(x,y,z,t) тех же переменных.

χ(x,y,z,t) = ψ(x,y,z,t).

Например: оператор может означать дифференцирование по какой-либо переменной:

χ(x,y,z,t) = ψ(x,y,z,t) = ∂(x,y,z,t)/∂x,

т. е. = ∂/∂x.

При построении операторов используется принцип − между операторами, описывающими частицы в квантовой механике, имеют место те же соотношения, что и между их аналогами в классической механике. Например, оператор полной энергии связан с операторами кинетической и потенциальной энергии соотношением = + .

Примеры некоторых операторов.

Оператор кинетической энергии :

Оператор Гамильтона (гамильтониан) − оператор полной энергии :

= + .

Если частица движется в потенциальном поле U(x,y,z), то оператор Гамильтона имеет вид