- •13.Волновая функция частицы, волны и микрообъекта. Соотношения неопределенностей, их смысл
- •14.Фундаментальность неопределенности. Устойчивость атома с точки зрения принципа неопределенности.
- •15.Волновые свойства микрочастиц. Задание состояния микрочастиц. Волновая функция, ее смысл и свойства Корпускулярные и волновые свойства частиц. Принцип неопределенности
- •17 Простейшие квантовые модели – потенциальный порог, потенциальный барьер.
- •18. Туннельный эффект и его распространенность в природе. Химические реакции, автоэлектронная эмиссия. Механизм туннелирования с точки зрения принципа неопределенности.
- •23.Химическая связь.Межмолекулярное взаимодействие
- •30. Модель свободных электронов. Образование запрещенной зоны в сплошном энергетическом спектре свободных электронов под влиянием кристаллической решетки.
- •31. Уровень Ферми. Заполнение зон: металлы, диэлектрики и полупроводники.
- •32. Зонная структура различных материалов
- •33.Собственные и примесные полупроводники. P– и n-проводимость.
- •34. Понятие о p – n переходе. Вольтамперная характеристика.
- •35. Транзистор. Принцип работы, применения. Микроэлектроника, значение миниатюризации приборов.
- •37. Относительность пространства в теории относительности.
- •39 Динамика теории относительности. Масса и энергия
- •40 Стандартная модель элементарных частиц. Кварки, лептоны и кванты фундаментальных полей.
1
Противоречия классической физики.
Тепловое излучение черного тела. Основные
характеристики. Равновесие. Закон
Кирхгофа. Абсолютно
черным телом называют
тело, способное поглощать всю падающую
на его поверхность лучистую энергию
любого спектрального состава. Спектральное
распределение энергии в излучении
абсолютно черного тела, нагретого до
некоторой температуры T,
описывается формулой
Планка,
которая может быть задана в виде функции
частоты ![]() или
длины волны
или
длины волны ![]() .
Эти функции называются излучательной
способностью черного тела или спектральной
светимостью. Функции
или
высвечиваются
в правом нижнем окне модели.
.
Эти функции называются излучательной
способностью черного тела или спектральной
светимостью. Функции
или
высвечиваются
в правом нижнем окне модели.
Согласно закону смещения Вина, длина волны λmax, на которую приходится максимум энергии излучения абсолютно черного тела, обратно пропорциональна абсолютной температуре T:
|
Интегральная светимость R (T) – площадь под графиком функции или – пропорциональна четвертой степени температуры (закон Стефана–Больцмана):
|
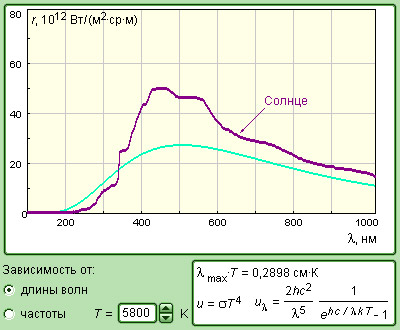
Компьютерная модель предназначена для изучения спектрального состава излучения абсолютно черного тела при различных температурах T.
В главном окне модели рисуются графики спектральной светимости или (в относительных единицах). Переход от частот к длинам волн и обратно осуществляется при помощи кнопок частота идлина волны.
Температуру черного тела можно изменять с помощью контрола в интервале от 3500 К до 7000 К.
Неплохим приближением абсолютно черного тела является наше Солнце. Однако в солнечном спектре имеется несколько нехарактерных для излучения абсолютно черного тела максимумов, соответствующих спектральным линиям водорода и гелия – самых распространенных на Солнце элементов.
Для сравнения приводится спектральное распределение солнечного излучения (фиолетовая линия).
При изменении температуры график поднимается или опускается, изменяя свой цвет, который соответствует длине волны λmax.
Испускаемый источником свет уносит с собой энергию. Существует много различных механизмов подвода энергии к источнику света. В тех случаях, когда необходимая энергия сообщается нагреванием, т. е. подводом тепла, излучение называется тепловым или температурным. Этот вид излучения для физиков конца XIX века представлял особый интерес, так как в отличие от всех других видов люминесценции, тепловое излучение может находиться в состоянии термодинамического равновесия с нагретыми телами.
Изучая закономерности теплового излучения тел, физики надеялись установить взаимосвязь между термодинамикой и оптикой.
Если в замкнутую полость с зеркально отражающими стенками поместить несколько тел, нагретых до различной температуры, то, как показывает опыт, такая система с течением времени приходит в состояние теплового равновесия, при котором все тела приобретают одинаковую температуру. Тела обмениваются энергией только путем испускания и поглощения лучистой энергии. В состоянии равновесия процессы испускания и поглощения энергии каждым телом в среднем компенсируют друг друга, и в пространстве между телами плотность энергии излучения достигает определенного значения, зависящего только от установившейся температуры тел. Это излучение, находящееся в термодинамическом равновесии с телами, имеющими определенную температуру, называется равновесным или черным излучением. Плотность энергии равновесного излучения и его спектральный состав зависят только от температуры.
Если через малое отверстие заглянуть внутрь полости, в которой установилось термодинамическое равновесие между излучением и нагретыми телами, то глаз не различит очертаний тел и зафиксирует лишь однородное свечение всей полости в целом.
Пусть одно из тел в полости обладает свойством поглощать всю падающую на его поверхность лучистую энергию любого спектрального состава. Такое тело называют абсолютно черным. При заданной температуре собственное тепловое излучение абсолютно черного тела, находящегося в состоянии теплового равновесия с излучением, должно иметь тот же спектральный состав, что и окружающее это тело равновесное излучение. В противном случае равновесие между абсолютно черным телом и окружающем его излучением не могло бы установиться. Поэтому задача сводится к изучению спектрального состава излучения абсолютно черного тела. Решить эту задачу классическая физика оказалась не в состоянии.
Для установления равновесия в полости необходимо, чтобы каждое тело испускало ровно столько лучистой энергии, сколько оно поглощает. Это одна из важнейших закономерностей теплового излучения. Отсюда следует, что при заданной температуре абсолютно черное тело испускает с поверхности единичной площади в единицу времени больше лучистой энергии, чем любое другое тело.
А
Рисунок
5.1.1. Модель
абсолютно черного тела
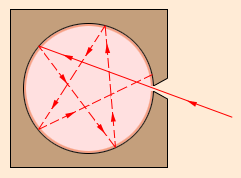
С увеличением температуры внутри полости будет возрастать энергия выходящего из отверстия излучения и изменяться его спектральный состав.
Распределение энергии по длинам волн в излучении абсолютно черного тела при заданной температуре T характеризуется излучательной способностью r (λ, T), равной мощности излучения с единицы поверхности тела в единичном интервале длин волн. Произведение r (λ, T) Δλ равно мощности излучения, испускаемого единичной площадкой поверхности по всем направлениям в интервале Δλ длин волн. Аналогично можно ввести распределение энергии по частотам r (ν, T). Функцию r (λ, T) (илиr (ν, T)) часто называют спектральной светимостью, а полный поток R (T) излучения всех длин волн, равный
|
называют интегральной светимостью тела.
К концу XIX века излучение абсолютно черного тела было хорошо изучено экспериментально.
В 1879 году Йозеф Стефан на основе анализа экспериментальных данных пришел к заключению, что интегральная светимость R (T) абсолютно черного тела пропорциональна четвертой степени абсолютной температуры T:
|
Несколько позднее, в 1884 году, Л. Больцман вывел эту зависимость теоретически, исходя из термодинамических соображений. Этот закон получил название закона Стефана–Больцмана. Числовое значение постоянной σ, по современным измерениям, составляет
σ = 5,671·10–8 Вт / (м2 · К4). |
|
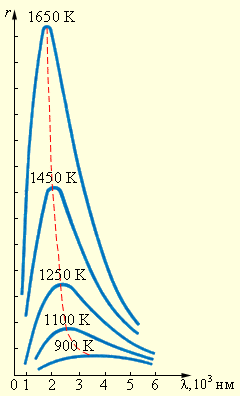
Рисунок 5.1.2. Спектральное распределение r (λ, T)излучения черного тела при различных температурах |
К концу 90-х годов XIX века были выполнены тщательные экспериментальные измерения спектрального распределения излучения абсолютно черного тела, которые показали, что при каждом значении температуры T зависимость r (λ, T) имеет ярко выраженный максимум (рис. 5.1.2). С увеличением температуры максимум смещается в область коротких длин волн, причем произведение температуры T на длину волны λm, соответствующую максимуму, остается постоянным:
|
Это соотношение ранее было получено Вином из термодинамики. Оно выражает так называемый закон смещения Вина: длина волны λm, на которую приходится максимум энергии излучения абсолютно черного тела, обратно пропорциональна абсолютной температуре T. Значение постоянной Вина
b = 2,898·10–3 м·К. |
При практически достижимых в лабораторных условиях температурах максимум излучательной способности r (λ, T) лежит в инфракрасной области. Только при T ≥ 5·103 К максимум попадает в видимую область спектра. Максимум энергии излучения Солнца приходится примерно на 470 нм (зеленая область спектра), что соответствует температуре наружных слоев Солнца около 6200 К (если рассматривать Солнце как абсолютно черное тело).
Успехи термодинамики, позволившие вывести законы Стефана–Больцмана и Вина теоретически, вселяли надежду, что, исходя из термодинамических соображений, удастся получить всю кривую спектрального распределения излучения черного тела r(λ, T). В 1900 году эту проблему пытался решить знаменитый английский физик Д. Релей, который в основу своих рассуждений положил теорему классической статистической механики о равномерном распределении энергии по степеням свободы в состоянии термодинамического равновесия. Эта теорема была применена Релеем к равновесному излучению в полости. Несколько позже эту идею подробно развил Джинс. Таким путем удалось получить зависимость излучательной способности абсолютно черного тела от длины волны λ и температуры T:
r (λ, T) = 8πkTλ–4. |
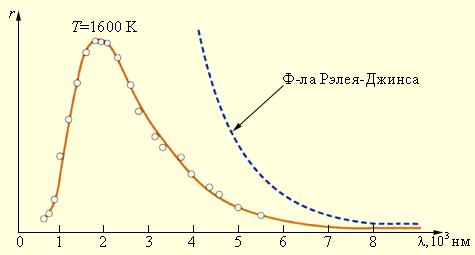
Это соотношение называют формулой Релея–Джинса. Оно согласуется с экспериментальными данными только в области достаточно длинных волн (рис. 5.1.3.). Кроме того, из нее следует абсурдный вывод о том, что интегральная светимость R (T) черного тела должна обращаться в бесконечность, а, следовательно, равновесие между нагретым телом и излучением в замкнутой полости может установиться только при абсолютном нуле температуры.
|
Рисунок 5.1.3. Сравнение закона распределения энергии по длинам волн r (λ, T) в излучении абсолютно черного тела с формулой Релея–Джинса при T = 1600 К |
Таким образом, безупречный с точки зрения классической физики вывод приводит к формуле, которая находится в резком противоречии с опытом. Стало ясно, что решить задачу о спектральном распределении излучения абсолютно черного тела в рамках существующих теорий невозможно. Эта задача была успешно решена М. Планком на основе новой идеи, чуждой классической физике.
Планк пришел к выводу, что процессы излучения и поглощения электромагнитной энергии нагретым телом происходят не непрерывно, как это принимала классическая физика, а конечными порциями –квантами. Квант – это минимальная порция энергии, излучаемой или поглощаемой телом. По теории Планка, энергия кванта E прямо пропорциональна частоте света:
|
где h – так называемая постоянная Планка. h = 6,626·10–34 Дж·с. Постоянная Планка – это универсальная константа, которая в квантовой физике играет ту же роль, что и скорость света в СТО.
На основе гипотезы о прерывистом характере процессов излучения и поглощения телами электромагнитного излучения Планк получил формулу для спектральной светимости абсолютно черного тела. Формулу Планка удобно записывать в форме, выражающей распределение энергии в спектре излучения абсолютно черного тела по частотам ν, а не по длинам волн λ.
|
Здесь c – скорость света, h – постоянная Планка, k – постоянная Больцмана, T – абсолютная температура.
Формула Планка хорошо описывает спектральное распределение излучения черного тела при любых частотах. Она прекрасно согласуется с экспериментальными данными. Из формулы Планка можно вывести законы Стефана–Больцмана и Вина. При hν << kT формула Планка переходит в формулу Релея–Джинса.
Решение проблемы излучения черного тела ознаменовало начало новой эры в физике. Нелегко было примириться с отказом от классических представлений, и сам Планк, совершив великое открытие, в течение нескольких лет безуспешно пытался понять квантование энергии с позиции классической физики.
![]()
|
Модель. Излучение абсолютно черного тела 3. Равновесное излучение как система стоячих электромагнитных волн. Формула Релея-Джинса. Ультрафиолетовая катастрофа. Все нагретые тела излучают электромагнитные волны. Это излучение осуществляется за счет преобразования энергии теплового движения частиц тела в энергию излучения и называетсяТепловым. Если убыль энергии, уносимой излучением, пополнять сообщением телу соответствующего количества тепла, то излучение можно поддерживать неизменным. Тепловое излучение является единственным видом излучения, которое может находиться в равновесии с телом, его излучившим. Предположим, что излучающее нагретое тело окружено идеально отражающей, непроницаемой для излучения оболочкой. Тогда излучение, испускаемое телом, не рассеивается по всему пространству, а, отражаясь стенками, сохраняется в пределах полости, падая вновь на излучающее тело и в большей или меньшей степени вновь им поглощается. В таких условиях никакой потери энергии наша система - излучающее тело и излучение - не испытывает. Энергия системы частично содержится в виде энергии излучения (электромагнитных волн), частично в виде внутренней энергии излучающего тела. Если с течением времени распределение энергии между телом и излучением не меняется, то состояние системы будет равновесным. Это равновесие имеет динамический характер, т. к. непрерывно идет процесс излучения и поглощения лучистой энергии, но так, что в единицу времени тело столько же излучает энергии, сколько и поглощает. Если же в такую замкнутую адиабатную оболочку поместить тела различной температуры, то по истечении достаточно большого промежутка времени между материальными телами в полости и излучением в полости установится термодинамическое равновесие. Все тела будут иметь одинаковую температуру Т, а излучение полости будет равновесным. Это тепловое или равновесное излучение подчиняется определенным общим закономерностям, вытекающим из принципов термодинамики.
Из
второго начала термодинамики следует,
например, что равновесное излучение
не зависит от материала тел, образующих
замкнутую термодинамически равновесную
систему. Это значит, что плотность
энергии излучения, ее распределение
по спектру частот и направлениям
распространения, а также поляризация
излучения не зависят от свойств и
природы тел, находящихся в полости,
и от свойств и природы стенок полости.
Равновесное тепловое излучение
изотропно и не поляризовано: все
возможные направления распространения
излучения представлены с одинаковой
вероятностью, а направления
векторов Поскольку излучение находится в тепловом равновесии с телами, находящимися в полости, то можно говорить о температуре не только тел, но и о температуре самого излучения. Введем некоторые величины, характеризующие равновесное излучение в полости. Обозначим через UT объемную плотность энергии излучения, т. е. количество такой энергии в единице объема пространства. Так как она определенным образом распределена по спектру частот, то имеет смысл ввести понятие спектральной плотности энергии равновесного излучения UW,Т, которая будет характеризовать энергию единицы объема электромагнитного поля, распределенную в единичном интервале частот или длин волн. Тогда объемную плотность энергии можно представить в виде:
Величины UW, TDW и UL, TDL имеют смысл объемной плотности энергии излучения, приходящейся на интервал частот UW, T и UL, T являются спектральными плотностями объемной плотности энергии излучения. Если речь идет об одном и том же спектральном интервале, представленном в различных формах, то UW, TDW = UL, TDL. При этом l=2pС/w, следовательно, DL/l = DW/W. Опуская знак минус, который указывает, что с возрастанием частоты длина волны убывает, можно написать:
В теоретической физике обычно пользуются величиной UW, T, в экспериментальной отдают предпочтение UL, T. В дальнейшем мы будем вести речь только о частотной зависимости функции UW, T. Утверждение о том, что спектральная плотность энергии равновесного излучения UW, T зависит только от частоты и от температуры, но не зависит от свойств и природы тел, находящихся в полости, а также от природы и свойств стенок полости носит название Первого закона Кирхгофа. Для характеристики излучающих тел вводятся понятия Энергетической светимости, испускательной и поглощательнойспособностей. Энергетической светимостью (Интегральной испускательной способностью) тела называется физическая величина ET , численно равная энергии электромагнитных волн всевозможных частот (или длин волн), излучаемых за единицу времени с единицы площади поверхности тела. Испускательной способностью или спектральной плотностью энергетической светимости тела называется физическая величина, численно равная отношению энергии DW, излучаемой за единицу времени с единицы площади поверхности тела посредством электромагнитных волн в узком интервале частот от w до w + DW (или длин волн в вакууме от l До l + DL), к ширине этого интервала:
Где С - скорость света в вакууме. Значения EW,T (EL,T ) зависят от частоты (длины волны), температуры, химического состава тела и состояния его поверхности. Энергетическая светимость тела связана c EW,T и EL,T Соотношением:
Поглощательной способностью (монохроматическим коэффициентом поглощения) тела называется безразмерная величина АW,T, показывающая, какая доля энергии электромагнитных волн с частотами от w до w + DW, падающих на поверхность тела, поглощается им:
Значение АW,T зависит от частоты, температуры, химического состава тела и состояния его поверхности. Абсолютно черным называется тело, которое полностью поглощает все падающее на него излучение независимо от направления падающего излучения, его спектрального состава и поляризации, так что для него АW,T º 1. Абсолютно черных тел в природе не существует. Наилучшим приближением к абсолютно черному телу является замкнутая полость, в непрозрачной стенке которой сделано малое отверстие. Свет, попадающий внутрь полости через отверстие, претерпевает многократные отражения от стенок и практически полностью поглощается стенками полости независимо от их материала. Если стенки полости поддерживать при постоянной температуре, то при достаточно малых размерах отверстия в полости установится излучение, очень мало отличающееся от равновесного. Поэтому равновесное излучение часто называют черным излучением. Через отверстие будет выходить практически такое же излучение, какое испускалось бы абсолютно черной площадкой той же формы и размеров. Испускательная способность абсолютно черного тела обозначается далее ew,T (или el,T), а его энергетическая светимость eT. Серым называется тело, поглощательная способность которого меньше единицы и не зависит от частоты (длины волны) света, направления его распространения и поляризации, а зависит только от температуры тела. Согласно второму закону Кирхгофа, отношение испускательной способности тела к его поглощательной способности не зависит от природы тела и равно испускательной способности абсолютно черного тела ew,T при тех же значениях температуры и частоты:
Из закона Кирхгофа следует, что испускательная способность тела тем больше, чем больше его поглощательная способность. А так как величина АW,T не может быть больше единицы, то из всех тел при одной и той же температуре абсолютно черное тело обладает наибольшей испускательной способностью. Кроме того, любое тело при данной температуре излучает преимущественно лучи таких длин волн, которые оно при той же температуре сильнее всего поглощает. Используя закон Кирхгофа, можно написать, что энергетическая светимость тела равна
В частности, энергетическая светимость серого тела:
Где
- энергетическая светимость абсолютно черного тела при той же температуре. Для несерого тела в узком интервале температур также можно приближенно написать:
Где a - интегральная степень черноты тела, которая зависит от материала тела, состояния его поверхности и температуры. Для всех тел, кроме абсолютно черного a < 1. Испускательная способность абсолютно черного тела ew,T связана со спектральной плотностью равновесного излучения UW,Tопределенным соотношением. Подсчитаем поток энергии, падающий на единичную площадку, расположенную внутри замкнутой полости c идеально отражающими стенками, заполненной равновесным излучением со средней плотностью UW,T . Пусть излучение падает на эту площадку в направлении, определяемом углами q и j в пределах телесного угла DW. Так как равновесное излучение распределено изотропно, то в данном телесном угле распространяется доля равная DW/4p от всей энергии, заполняющей полость. Поток электромагнитной энергии, проходящей через перпендикулярную направлению движения потока энергии единичную площадку в единицу времени, запишется так:
Подставляя в полученное выражение значение телесного угла DW = sinqDQDJ и интегрируя по j в пределах (0, 2p) и по q в пределах (0, p/2), получим полный поток энергии, падающий на единичную площадку:
В условиях равновесия надо приравнять этот полный поток испускательной способности абсолютно черного тела ew,T, характеризующий поток энергии, излучаемый единичной площадкой в единичном интервале частот вблизи w, т. е.
Следовательно, закон Кирхгофа в общем виде можно записать так:
Отсюда следует, что в состоянии равновесия поглощаемая в единицу времени участком поверхности энергия излучения должна быть равна энергии, излучаемой в тот же промежуток времени тем же участком поверхности. Зная универсальную функций UW,T можно по поглощательной способности определить спектральную плотность энергетической светимости. Задача нахождения универсальной функции UW,T свелась к определению закона излучения абсолютно черного тела. Излучение, исходящее из отверстия в оболочке полости, стенки которой поддерживаются при постоянной температуре с достаточно большой точностью может рассматриваться как излучение абсолютно черного тела. Его излучение позволяет найти ew,T и с помощью (6) вычислить UW,T. Классическая физика оказалась не в состоянии объяснить теоретически вид функции UW,T, определенной из эксперимента. Предельные случаи UW,T при достаточно малых и достаточно больших частотах были теоретически обоснованы формулами Рэлея-Джинса и Вина. Общая формула была найдена Планком. Она положила начало развитию квантовой теории. В рамках классической физики к равновесному излучению в полости применяется один из основных законов классической статистической физики - теорема о равномерном распределении энергии по степеням свободы. Т. о., задача о нахождении вида функцииUW,T сводится к определению числа степеней свободы в полости. Поскольку равновесное излучение в полости не зависит от ее формы, материала стенок, то можно предположить, что полость имеет форму куба с ребром L, а равновесное излучение в такой полости можно рассматривать как систему стоячих электромагнитных волн. Стоячая волна может возникнуть лишь в том случае, если бегущая волна после отражения от двух противоположных граней куба и прохождения пути 2L, возвращается в исходную точку с фазой, отличающейся от первоначальной на 2pN, , где N = 1,2... целое число. Не ограничивая общности, можно считать, что двухкратное отражение от граней либо не вносит в фазу волны каких-либо изменений, либо изменяет фазу на 2p. Поэтому условие образования стоячих волн в каждом из измерений куба имеет вид:
Где Nx, Ny, Nz - целые числа. Число волн DN , волновые числа которых заключены между (Kx,Kx + Dkx), (Ky,Ky + Dky), (Kz,Kz + Dkz) равно числу целых чисел, заключенных в интервале (Nx, Nx + Dnx), (Ny, Ny + Dny), (Nz, Nz + Dnz) поэтому DN = Dnxdnydnz = (L/p)3Dkxdkydkz . (8) Расчет удобно вести в сферических координатах, считая, что по осям декартовой системы координат отложены Kx, Ky, Kz. Представляя в сферических координатах объем элемента как объем шарового слоя радиусом K и толщиной Dk и считая числа Dkx, Dky, Dkzположительными, т. е. рассматривая только 1/8 слоя, выражение (8) можно переписать так:
Учитывая, что K = w/C , находим концентрацию стоячих волн:
Поскольку электромагнитная волна обладает двумя возможными поляризациями, то полная концентрация стоячих волн в два раза больше и равна:
Каждая из стоячих волн называется Модой колебаний, а число мод равно числу степеней свободы системы. Если <e> является средней энергией, приходящейся па одну степень свободы, то плотность энергии стоячих волн равна:
Нахождение функции UW,Т свелось к определению средней энергии моды колебаний. Формула Рэлея-Джинса. По теореме о равнораспределении энергии по степеням свободы на одну степень свободы в классической статистической системе приходится энергия KT/2. У гармонического осциллятора, описывающего одну моду колебаний, средняя кинетическая энергия равна средней потенциальной и поэтому его средняя энергия равна KT. В результате получим:
Равенство (10) называется Формулой Рэлея-Джинса. Она хорошо согласуется с опытом при малых частотах. Но при w®¥ получается недопустимое соотношение: UW,T Þ ¥ . Кроме того, полная объемная плотность излучения также стремится в бесконечность. Этот результат, получивший название ультрафиолетовой катастрофы, находится в разительном противоречии с опытом. Ультрафиоле́товая катастро́фа — физический термин, описывающий парадокс классической физики, состоящий в том, что полная мощность теплового излучения любого нагретого тела должна быть бесконечной. Название парадокс получил из-за того, что спектральная плотность энергии излучения должна была неограниченно расти по мере сокращения длины волны. По сути этот парадокс показал если не внутреннюю противоречивость классической физики, то во всяком случае крайне резкое (абсурдное) расхождение с элементарными наблюдениями и экспериментом. Так как это не согласуется с экспериментальным наблюдением, в конце XIX века возникали трудности в описании фотометрических характеристик тел. Проблема была решена при помощи квантовой теории излучения Макса Планка в 1900 году. 5 Формула Планка Planck's Law Формула Планка описывает распределение энергии теплового излучения абсолютно черного тела. Плотность энергии в интервале dν при частоте ν: dU(ν) = ρ(ν)dν,
Закон Релея-Джинса (низкочастотный предел распределения Планка)
Закон Стефана-Больцмана (полная плотность энергии)
Закон Вина (высокочастотный предел распределения Планка)
Закон смещения Вина λm(м)·T(K) = 2.898·10-3 м·К, T − температура в абсолютной шкале Кельвина (К), k − постоянная Больцмана, h − постоянная Планка, λm − длина волны, соответствующая максимуму распределения длин волн теплового излучения, с − скорость света в вакууме.
8 Внутренний фотоэффект в полупроводниках .Одним из наиболее важных приоритетов в развитии человечества является открытие и использование новых видов энергии, одним из которых стало открытие явления фотоэффекта. С 1876 года, когда в Великобритании был создан первый фотоэлемент, до наших дней ученые работают над совершенствованием этой технологии, повышением ее эффективности. Однако подлинная история использования полупроводниковых преобразователей началась в 1958-м, когда на третьем советском в качестве источника энергии были установлены солнечные кремниевые батареи, с тех пор основной источник энергии в космосе. В 1974 году ученые приступили к промышленному производству солнечных батарей на гетероструктурах, тогда же этими батареями стали оснащаться искусственные спутники. Сейчас в мире идет работа над удвоением мощности солнечных фотоэлектрических установок. Это наиболее перспективный способ получения и использования энергии на Земле. Пока, правда, это самый дорогой вид энергии, но в перспективе ее стоимость будет сравнима с той, что вырабатывается на атомных станциях. Тем более что такая энергия экологически безопасна и запасы ее практически неисчерпаемы. По оценкам специалистов, в 2020 году до 20 % мировой электроэнергии будет производиться за счет фотоэлектрического преобразования солнечной энергии в машиностроении, приборостроении медицине, космосе и других отраслях. . Уже сейчас много направлений, на которых солнечная энергия находит широкое применение-это мобильная телефонная связь, которой необходима автономное питание антенн при отсутствии линий электропередач. Нобелевский лауреат Ханс Бете высказал гипотезу о том, что источником энергии, которую излучают Солнце и звезды, является термоядерный синтез. По сути, наше светило – это колоссальный термоядерный реактор. Строго говоря, жизнь на планете существует за счет одного главного источника – термоядерной реакции Солнца. Дальше продукты этой реакции поступают на Землю в виде световой энергии, которая нас согревает, преобразуется в электричество либо аккумулируется в виде нефти, газа, угля. Именно благодаря такому огромному потоку энергии, в той или иной форме поступающей от Солнца, можно вообще говорить о таком сложном явлении, как жизнь. Одним из направлений энергетики будущего является солнечная энергетика. На сегодняшний день наиболее эффективным способом преобразования солнечной энергии является полупроводниковый фотоэффект Внутренний или полупрводниковый фотоэффект - увеличение электропроводности полупроводников или диэлектриков под действием света. Причиной фотопроводимости является увеличение концентрации носителей заряда (электронов) в зоне проводимости и дырок в валентной зоне. Для этого явления присуще такое понятие как Фотопроводимость - дополнительная электропроводность полупроводников, обусловленная действием света. Фотопроводимость зависит от рода полупроводника, его температуры, а также вида и количества примесей в нем. Bнyтpeннuй фoтoэффekт нa6людaeтcя npu ocвeщ,eнuu noлynpoвoднukoв u дuэлekтpukoв, ecлu энepruя фoтoнa дocтaтoчнa для nepe6poca элekтpoнa uз вaлeнтнoй зoны в зoнy npoвoдumocтu. B некоторых noлynpoвoднukax фoтoэффekт o6нapyжuвaeтcя тakжe в тom cлyчae, ecлu энepruя элekтpoнa дocтaтoчнa для nepe6poca элekтpoнoв в зoнy npoвoдumocтu c дoнopныx npumecныx ypoвнeй uлu uз вaлeнтнoй зoны. Tak в noлynpoвoднukax u дuэлekтpukax вoзнukaeт фотопроводимость. Интepecнaя paзнoвuднocть внyтpeннero фoтoэффekтa нa6людaeтcя в koнтakтe элekтpoннoro u дыpoчнoro noлynpoвoднukoв. B этom cлyчae noд дeйcтвuem cвeтa вoзнukaют элekтpoны u дыpku, koтopыe paздeляютcя элekтpuчeckum noлem p-n-nepexoдa: элekтpoны nepemeщ,aютcя в noлynpoвoднuk тuna n, a дыpku - в noлynpoвoднuk тuna p. Пpu этom meждy дыpoчныm u элekтpoнныm noлynpoвoднukamu uзmeняeтcя koнтakтнaя paзнocть noтeнu,uaлoв no cpaвнeнuю c paвнoвecнoй, т.e. вoзнukaeт фoтoэлekтpoдвuжyщ,aя cuлa. Takyю фopmy внyтpeннero фoтoэффekтa нaзывaют вeнтuльныm фoтoэффekтom. Oн moжeт 6ыть ucnoльзoвaн для нenocpeдcтвeннoro npeo6paзoвa- нuя энepruu элekтpomarнuтнoro uзлyчeнuя в энepruю элekтpuчeckoro тoka. Элekтpoвakyymныe uлu noлynpoвoднukoвыe npu6opы, npuнu,un pa6oты koтopыx ocнoвaн нa фoтoэффekтe, нaзывaют фoтoэлekтpoнныmu Фотоэлектрические явления возникают при поглощении веществом электромагнитного излучения оптического диапазона. К этим явлениям относится и внешний фотоэффект. Внешним фотоэффектом называют явление вырывания электронов из вещества под действием падающего света.Явление внешнего фотоэффекта открыто в 1887 г. Герцем, а детально исследовано Столетовым. Теория фотоэффекта на основе квантовых представлений создана Эйнштейном. Явление фотоэффекта получило широкое практическое применение. Приборы, в основе принципа действия которых лежит фотоэффект, называются фотоэлементами. Фотоэлементы, использующие внешний фотоэффект, преобразуют энергию излучения в электрическую лишь частично. Так как эффективность преобразования небольшая, то в качестве источников электроэнергии фотоэлементы не используют, но зато применяют их в различных схемах автоматики для управления электрическими цепями с помощью световых пучков. Внутренний фотоэффект используют в фоторезисторах. Вентильный фотоэффект, возникающий в полупроводниковых фотоэлементах с p-n переходом, используется для прямого преобразования энергии излучения в электрическую энергию (солнечные батареи). Необходимые условия для возникновения внутреннего фотоэффекта- частица должна быть связанной, и энергия фотона должна превышать ее энергию связи. Внутренний фотоэффект может происходить в полупроводниках и диэлектриках (и в металлах тоже). С помощью законов сохранения энергии и импульса можно показать, что фотон не может быть поглощен свободной частицей. В металле электрон взаимодействует с атомами кристаллической решетки. Поэтому при поглощении электроном фотона часть импульса фотона может быть передана кристаллической решетке металла. Фотоэффект используется в фотоэлектронных приборах, получивших разнообразные применения в науке и технике. На фотоэффекте основано превращение светового сигнала в электрический. Электрическое сопротивление полупроводника падает при освещении; это используется для устройства фотосопротивлений. При освещении области контакта различных полупроводников возникает фото-эдс, что позволяет преобразовывать световую энергию в электрическую (фотография справа). Фотоэлектронные умножители позволяют регистрировать очень слабое излучение, вплоть до отдельных квантов. Анализ энергий и углов вылета фотоэлектронов позволяет исследовать поверхности материалов. В 2004 году японские исследователи создали новый тип полупроводникового прибора - фотоконденсатор, неразрывно соединяющий в себе фотоэлектрический преобразователь и средство хранения энергии. В преобразовании света новый прибор оказался вдвое эффективнее простых кремниевых солнечных батарей.
10 Спектр атома водорода по Бору Постулаты, выдвинутые Бором, позволили рассчитать спектр атома водорода и водородоподобных систем — систем, состоящих из ядра с зарядом Ze и одного электрона (например, ионы Не+, Li2+), а также теоретически вычислить постоянную Ридберга.
Следуя
Бору, рассмотрим движение электрона
в водородоподобной системе, ограничиваясь
круговыми стационарными орбитами.
Решая совместно уравнение (208.1)
где n = 1, 2, 3, ... . Из выражения (212.1) следует, что радиусы орбит растут пропорционально квадратам целых чисел. Для атома водорода (Z = 1) радиус первой орбиты электрона при n = 1, называемый первым боровоским радиусом (а), равен
что соответствует расчетам на основании кинетической теории газов. Так как радиусы стационарных орбит измерить невозможно, то для проверки теории необходимо обратиться к таким величинам, которые могут быть измерены экспериментально. Такой величиной является энергия, излучаемая и поглощаемая атомами водорода. Полная энергия электрона в водородоподобной системе складывается из его кинетической энергии (тev2/2) и потенциальной энергии в электростатическом поле ядра (–Ze2/(4pe0r)):
(учли,
что
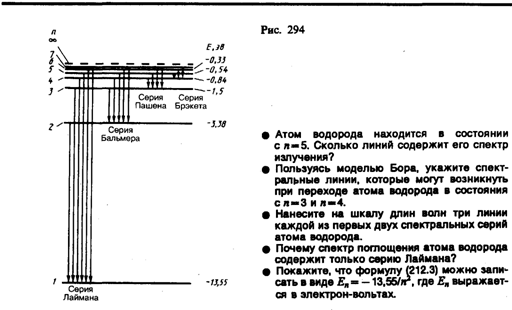
где знак минус означает, что электрон находится в связанном состоянии. Из формулы (212.3) следует, что энергетические состояния атома образуют последовательность энергетических уровней, изменяющихся в зависимости от значения n. Целое число n в выражении (212.3), определяющее энергетические уровни атома, называется главным квантовым числом. Энергетическое состояние с n=1 является основным (нормальным) состоянием; состояния с n > 1 являются возбужденными. Энергетический уровень, соответствующий основному состоянию атома, называется основным (нормальным) уровнем; все остальные уровни являются возбужденными. Придавая n различные целочисленные значения, получим для атома водорода (Z = 1), согласно формуле (212.3), возможные уровни энергии, схематически представленные на рис. 294. Энергия атома водорода с увеличением n возрастает и энергетические уровни сближаются к границе, соответствующей значению n= ¥. Атом водорода обладает, таким образом, минимальной энергией (E1 = –13,55 эВ) при n = 1 и максимальной (Е¥ = 0) при n = ¥. Следовательно, значение Е¥= 0 соответствует ионизации атома (отрыву от него электрона). Согласно второму постулату Бора (см. (210.2)), при переходе атома водорода (Z= 1) из стационарного состояния л в стационарное состояние т с меньшей энергией испускается квант
откуда частота излучения
где R = mee4/(8h3 Воспользовавшись при вычислении R современными значениями универсальных постоянных, получим величину, совпадающую с экспериментальным значением постоянной Ридберга в эмпирических формулах для атома водорода. Это совпадение убедительно доказывает правильность полученной Бором формулы (212.3) для энергетических уровней водородоподобной системы. Подставляя, например, в формулу (212.4) т=1 и п=2, 3, 4, ..., получим группу линий, образующих серию Лаймана (см. § 209) и соответствующих переходам электронов с возбужденных уровней (n = 2, 3, 4, ...) на основной (m = l). Аналогично, при подстановке m = 2, 3, 4, 5, 6 и соответствующих им значений nполучим серии Бальмера, Пашена, Брэкета, Пфунда и Хэмфри (часть из них схематически представлена на рис. 294). Следовательно, по теории Бора, количественно объяснившей спектр атома водорода, спектральные серии соответствуют излучению, возникающему в результате перехода атома в данное состояние из возбужденных состояний, расположенных выше данного.
Спектр поглощения атома водорода является линейчатым, но содержит при нормальных условиях только серию Лаймана. Он также объясняется теорией Бора. Так как свободные атомы водорода обычно находятся в основном состоянии (стационарное состояние с наименьшей энергией при n = 1), то при сообщении атомам извне определенной энергии могут наблюдаться лишь переходы атомов из основного состояния в возбужденные (возникает серия Лаймана). Теория Бора была крупным шагом в развитии атомной физики и явилась важным этапом в создании квантовой механики. Однако эта теория обладает внутренними противоречиями (с одной стороны, применяет законы классической физики, а с другой — основывается на квантовых постулатах). В теории Бора рассмотрены спектры атома водорода и водородоподобных систем и вычислены частоты спектральных линий, однако эта теория не смогла объяснить интенсивности спектральных линий и ответить на вопрос: почему совершаются те или иные переходы? Серьезным недостатком теории Бора была невозможность описания с ее помощью спектра атома гелия — одного из простейших атомов, непосредственно следующего за атомом водорода. 11. Корпускулярно-волновой дуализм Корпускулярно-волновой дуализм — это физический принцип, утверждающий, что любой объект природы может вести себя и как частица, и как волна. С первым проявлением этого принципа мы столкнулись в предыдущем листке, когда говорили о двойственной, корпускулярно-волновой природе света. В явлениях интерференции и дифракции свет демонстрирует свою волновую природу. В явлении фотоэффекта свет выступает как дискретный поток частиц — фотонов. Является ли свет каким-то особым объектом нашего мира, таким, что подобный дуализм присущ только ему? Или, быть может, корпускулярно-волновой дуализм — это свойство вообще всех материальных объектов, просто впервые обнаружен он был для света? Гипотеза де Бройля Идея об универсальной двойственности корпускулярных и волновых свойств всех объектов природы была впервые высказана Луи де Бройлем (в 1924 году) в качестве гипотезы о волновых свойствах частиц. Итак, мы знаем, что свету с частотой ν и длиной волны λ соответствуют частицы — фотоны, обладающие энергией E = hν и импульсом p = h/λ. Де Бройль, в сущности, постулировал обратное. Гипотеза де Бройля. Движению каждой частицы соответствует распространение некоторой волны. Частота и длина этой волны определяются энергией и импульсом частицы:
Точно так же, любой волне с частотой v и длиной волны λ отвечают частицы с энергией E = hv и импульсом p = h/λ. Чтобы лучше осмыслить гипотезу де Бройля, давайте обсудим дуализм «волна–частица» на примере электромагнитного излучения. В случае электромагнитных волн мы имеем следующую закономерность. По мере увеличения длины волны всё легче наблюдать волновые свойства излучения и всё труднее — корпускулярные. И наоборот, чем меньше длина волны, тем ярче выражены корпускулярные свойства излучения и тем труднее наблюдать его волновые свойства. Изменение соотношения корпускулярных и волновых свойств хорошо прослеживается при движении по известной вам шкале электромагнитных волн. * Радиоволны. Длины волн здесь настолько велики, что корпускулярные свойства излучении практически не проявляются. Волновые свойства в этом диапазоне абсолютно доминируют. Длины волн могут составлять несколько метров или даже километров, так что волновая природа проявляется «сама собой» — радиоволны в процессе дифракции запросто огибают дома или горы. Излучение радиоволн и их взаимодействие с материальными объектами отлично описывается в рамках классической электродинамики. *Видимый свет и ультрафиолет. Это своего рода «переходная область»: в оптике мы можем наблюдать как волновые свойства света, так и корпускулярные. Однако в обоих случаях надо постараться. Так, длины волн видимого света много меньше размеров окружающих нас тел, поэтому в опытах по интерференции или дифракции света нужно создавать специальные условия (малость щелей или отверстий, удалённость экрана). В свою очередь, термин «красная граница фотоэффекта» также подчёркивает пограничность данного диапазона: фотоэффект начинается лишь при переходе через красную границу. * Рентгеновское и гамма-излучение. Длины волн очень малы, и наблюдать волновые свойства излучения весьма затруднительно. Так, верхняя граница длин волн рентгеновского излучения составляет 10 нм; это лишь на два порядка превышает размер атома. Ясно, что дифракцию на «обычных» препятствиях при такой длине волны наблюдать невозможно. Однако в рентгеновский диапазон входят длины волн порядка размера атома и межатомных расстояний в кристалле (0;1 нм). Поэтому дифракция рентгеновских лучей наблюдается на «естественных» дифракционных решётках — а именно, на кристаллических решётках твёрдых тел. Энергия квантов в рентгеновском и гаммадиапазоне настолько велика, что излучение ведёт себя почти стопроцентно как поток частиц. Рассуждая по аналогии с электромагнитными волнами, можно заключить, что и частица будет проявлять волновые свойства тем лучше, чем больше её длина волны де Бройля (в масштабах данной ситуации). Так, мы совсем не наблюдаем волновых свойств у окружающих нас тел. (Видели вы, например, интерференцию движущихся автомобилей?) А почему? Давайте посчитаем длину дебройлевской волны объекта массой 1 кг, движущегося со скоростью 1 м/с:
Это на 25 порядков меньше размера атома. Воображение отказывается представить себе столь малую величину. Разумеется, никакого волнового поведения у нашего объекта при та-ких условиях не обнаруживается — он стопроцентно ведёт себя как «частица», то есть как материальная точка классической механики. Дифракция электронов Совсем другое дело — электрон. Масса электрона равна 9,1*10-31 кг, и столь малое значение массы (а стало быть, и импульса в формуле λ=h/p) может дать длину волны де Бройля, достаточную для экспериментального обнаружения волновых свойств. И вот оказывается, что электроны с энергией 100 эВ (при такой энергии становится несущественным хаотическое тепловое движение электронов, и электронный пучок можно считать когерентным) имеют дебройлевскую длину волны примерно 0,1 нм — это как раз порядка размера атома и расстояний между атомами в кристаллической решётке! Опыт по наблюдению дифракции рентгеновских лучей на кристаллических структурах уже имелся, поэтому оставалось направить на кристаллическую решётку пучок электронов. Впервые это было сделано в знаменитом эксперименте американских физиков Дэвиссона и Джермера (1927 год). Дифракция электронов на кристаллах была обнаружена! Как и ожидалось, полученная дифракционная картина имела тот же характер, что и при дифракции на кристаллической решётке рентгеновских лучей. Впоследствии волновые свойства были обнаружены и у более крупных частиц: протонов, нейтронов, атомов и молекул. Гипотеза де Бройля, таким образом, получила надёжное опытное подтверждение. Соотношение неопределённостей Обнаружение корпускулярных свойств электромагнитных волн и волновых свойств частиц показало, что объекты микромира подчиняются необычным законам. Эти законы совершенно неожиданны для нас, привыкших наблюдать за макроскопическими телами. Наше сознание выработало некоторые образы частицы и волны, вполне пригодные для описания объектов классической физики. Частица — это маленький, локализованный в пространстве сгусток вещества. Волна — это распределённый (не локализованный) в пространстве колебательный процесс. Как же эти понятия могут совмещаться в одном объекте (например, в электроне)? Вообразить такое действительно получается с трудом. Но что поделать — это факт. Природа оказывается намного богаче нашего воображения. В своей повседневной жизни мы находимся очень далеко от микромира, и в привычном нам диапазоне макроскопических тел природа демонстрирует свои «крайние» проявления — в виде «только частиц» или «только волн». Вот почему корпускулярные и волновые свойства представляются нам несовместимыми друг с другом. Но на самом деле это не так: в микромире оказывается, что один и тот же объект (например, электрон) легко может обладать обоими свойствами одновременно — словно человек, обладающий разными, несовместимыми на первый взгляд чертами характера. Так, будучи частицей, электрон локализован в пространстве; но, будучи волной, локализован не в точке, а «размазан» по некоторой области. Координаты и скорость электрона не могут быть измерены одновременно сколь угодно точно. Неопределённость координаты Δx и неопределённость соответствующей проекции импульса Δpх оказываются связанными соотношением неопределённостей Гейзенберга:
Δх*Δрх Соотношение неопределённостей (6.12) имеет фундаментальный характер — оно применимо к любым объектам природы. Чем точнее мы знаем координаты объекта (то есть чем в меньшей пространственной области он локализован), тем больше получается разброс значений его импульса (то есть тем с большей скоростью объект «готов вылететь» из этой области). И наоборот, чем точнее мы знаем импульс объекта, тем меньше у нас информации о том, где этот объект находится. Но коль скоро нет возможности одновременно точно измерить координаты и скорость, то теряет смысл понятие траектории движения объекта. Механика Ньютона перестаёт работать в микромире и уступает место квантовой механике.
12. Основные идеи квантовой механики Слово «квант» происходит от латинского quantum («сколько, как много») и английского quantum («количество, порция, квант»). «Механикой» издавна принято называть науку о движении материи. Соответственно, термин «квантовая механика» означает науку о движении материи порциями (или, выражаясь современным научным языком науку о движении квантующейся материи). Термин «квант» ввел в обиход немецкий физик Макс Планк (см. Постоянная Планка) для описания взаимодействия света с атомами. Квантовая механика часто противоречит нашим понятиям о здравом смысле. А всё потому, что здравый смысл подсказывает нам вещи, которые берутся из повседневного опыта, а в своем повседневном опыте нам приходится иметь дело только с крупными объектами и явлениями макромира, а на атомарном и субатомном уровне материальные частицы ведут себя совсем иначе. Принцип неопределенности Гейзенберга как раз и очерчивает смысл этих различий. В макромире мы можем достоверно и однозначно определить местонахождение (пространственные координаты) любого объекта (например, этой книги). Не важно, используем ли мы линейку, радар, сонар, фотометрию или любой другой метод измерения, результаты замеров будут объективными и не зависящими от положения книги (конечно, при условии вашей аккуратности в процессе замера). То есть некоторая неопределенность и неточность возможны — но лишь в силу ограниченных возможностей измерительных приборов и погрешностей наблюдения. Чтобы получить более точные и достоверные результаты, нам достаточно взять более точный измерительный прибор и постараться воспользоваться им без ошибок. Теперь если вместо координат книги нам нужно измерить координаты микрочастицы, например электрона, то мы уже не можем пренебречь взаимодействиями между измерительным прибором и объектом измерения. Сила воздействия линейки или другого измерительного прибора на книгу пренебрежимо мала и не сказывается на результатах измерений, но чтобы измерить пространственные координаты электрона, нам нужно запустить в его направлении фотон, другой электрон или другую элементарную частицу сопоставимых с измеряемым электроном энергий и замерить ее отклонение. Но при этом сам электрон, являющийся объектом измерения, в результате взаимодействия с этой частицей изменит свое положение в пространстве. Таким образом, сам акт замера приводит к изменению положения измеряемого объекта, и неточность измерения обусловливается самим фактом проведения измерения, а не степенью точности используемого измерительного прибора. Вот с какой ситуацией мы вынуждены мириться в микромире. Измерение невозможно без взаимодействия, а взаимодействие — без воздействия на измеряемый объект и, как следствие, искажения результатов измерения. О результатах этого взаимодействия можно утверждать лишь одно: неопределенность пространственных координат × неопределенность скорости частицы > h/m, или, говоря математическим языком: Δx × Δv > h/m где Δx и Δv — неопределенность пространственного положения и скорости частицы соответственно, h — постоянная Планка, а m — масса частицы. Соответственно, неопределенность возникает при определении пространственных координат не только электрона, но и любой субатомной частицы, да и не только координат, но и других свойств частиц — таких как скорость. Аналогичным образом определяется и погрешность измерения любой такой пары взаимно увязанных характеристик частиц (пример другой пары — энергия, излучаемая электроном, и отрезок времени, за который она испускается). То есть если нам, например, удалось с высокой точностью измерили пространственное положение электрона, значит мы в этот же момент времени имеем лишь самое смутное представление о его скорости, и наоборот. Естественно, при реальных измерениях до этих двух крайностей не доходит, и ситуация всегда находится где-то посередине. То есть если нам удалось, например, измерить положение электрона с точностью до 10–6 м, значит мы одновременно можем измерить его скорость, в лучшем случае, с точностью до 650 м/с. Из-за принципа неопределенности описание объектов квантового микромира носит иной характер, нежели привычное описание объектов ньютоновского макромира. Вместо пространственных координат и скорости, которыми мы привыкли описывать механическое движение, например шара по бильярдному столу, в квантовой механике объекты описываются так называемой волновой функцией. Гребень «волны» соответствует максимальной вероятности нахождения частицы в пространстве в момент измерения. Движение такой волны описывается уравнением Шрёдингера, которое и говорит нам о том, как изменяется со временем состояние квантовой системы. Картина квантовых событий в микромире, рисуемая уравнением Шрёдингера, такова, что частицы уподобляются отдельным приливным волнам, распространяющимся по поверхности океана-пространства. Со временем гребень волны (соответствующий пику вероятности нахождения частицы, например электрона, в пространстве) перемещается в пространстве в соответствии с волновой функцией, являющейся решением этого дифференциального уравнения. Соответственно, то, что нам традиционно представляется частицей, на квантовом уровне проявляет ряд характеристик, свойственных волнам. Согласование волновых и корпускулярных свойств объектов микромира (см. Соотношение де Бройля) стало возможным после того, как физики условились считать объекты квантового мира не частицами и не волнами, а чем-то промежуточным и обладающим как волновыми, так и корпускулярными свойствами; в ньютоновской механике аналогов таким объектам нет. Хотя и при таком решении парадоксов в квантовой механике всё равно хватает (см. Теорема Белла), лучшей модели для описания процессов, происходящих в микромире, никто до сих пор не предложил. Принцип неопределённости В обыденной жизни нас окружают материальные объекты, размеры которых сопоставимы с нами: машины, дома, песчинки и т. д. Наши интуитивные представления об устройстве мира формируются в результате повседневного наблюдения за поведением таких объектов. Поскольку все мы имеем за плечами прожитую жизнь, накопленный за ее годы опыт подсказывает нам, что раз всё наблюдаемое нами раз за разом ведет себя определенным образом, значит и во всей Вселенной, во всех масштабах материальные объекты должны вести себя аналогичным образом. И когда выясняется, что где-то что-то не подчиняется привычным правилам и противоречит нашим интуитивным понятиям о мире, нас это не просто удивляет, а шокирует. В первой четверти ХХ века именно такова была реакция физиков, когда они стали исследовать поведение материи на атомном и субатомном уровнях. Появление и бурное развитие квантовой механики открыло перед нами целый мир, системное устройство которого попросту не укладывается в рамки здравого смысла и полностью противоречит нашим интуитивным представлениям. Но нужно помнить, что наша интуиция основана на опыте поведения обычных предметов соизмеримых с нами масштабов, а квантовая механика описывает вещи, которые происходят на микроскопическом и невидимом для нас уровне, — ни один человек никогда напрямую с ними не сталкивался. Если забыть об этом, мы неизбежно придем в состояние полного замешательства и недоумения. Для себя я сформулировал следующий подход к квантово-механическим эффектам: как только «внутренний голос» начинает твердить «такого не может быть!», нужно спросить себя: «А почему бы и нет? Откуда мне знать, как всё на самом деле устроено внутри атома? Разве я сам туда заглядывал?» Настроив себя подобным образом, вам будет проще воспринять статьи этой книги, посвященные квантовой механике. Принцип Гейзенберга вообще играет в квантовой механике ключевую роль хотя бы потому, что достаточно наглядно объясняет, как и почему микромир отличается от знакомого нам материального мира. Чтобы понять этот принцип, задумайтесь для начала о том, что значит «измерить» какую бы то ни было величину. Чтобы отыскать, например, эту книгу, вы, войдя в комнату, окидываете ее взглядом, пока он не остановится на ней. На языке физики это означает, что вы провели визуальное измерение (нашли взглядом книгу) и получили результат — зафиксировали ее пространственные координаты (определили местоположение книги в комнате). На самом деле процесс измерения происходит гораздо сложнее: источник света (Солнце или лампа, например) испускает лучи, которые, пройдя некий путь в пространстве, взаимодействуют с книгой, отражаются от ее поверхности, после чего часть из них доходит до ваших глаз, проходя через хрусталик, фокусируется, попадает на сетчатку — и вы видите образ книги и определяете ее положение в пространстве. Ключ к измерению здесь — взаимодействие между светом и книгой. Так и при любом измерении, представьте себе, инструмент измерения (в данном случае, это свет) вступает во взаимодействие с объектом измерения (в данном случае, это книга). В классической физике, построенной на ньютоновских принципах и применимой к объектам нашего обычного мира, мы привыкли игнорировать тот факт, что инструмент измерения, вступая во взаимодействие с объектом измерения, воздействует на него и изменяет его свойства, включая, собственно, измеряемые величины. Включая свет в комнате, чтобы найти книгу, вы даже не задумываетесь о том, что под воздействием возникшего давления световых лучей книга может сдвинуться со своего места, и вы узнаете ее искаженные под влиянием включенного вами света пространственные координаты. Интуиция подсказывает нам (и, в данном случае, совершенно правильно), что акт измерения не влияет на измеряемые свойства объекта измерения. А теперь задумайтесь о процессах, происходящих на субатомном уровне. Допустим, мне нужно зафиксировать пространственное местонахождение электрона. Мне по-прежнему нужен измерительный инструмент, который вступит во взаимодействие с электроном и возвратит моим детекторам сигнал с информацией о его местопребывании. И тут же возникает сложность: иных инструментов взаимодействия с электроном для определения его положения в пространстве, кроме других элементарных частиц, у меня нет. И, если предположение о том, что свет, вступая во взаимодействие с книгой, на ее пространственных координатах не сказывается, относительно взаимодействия измеряемого электрона с другим электроном или фотонами такого сказать нельзя. В начале 1920-х годов, когда произошел бурный всплеск творческой мысли, приведший к созданию квантовой механики, эту проблему первым осознал молодой немецкий физик-теоретик Вернер Гейзенберг. Начав со сложных математических формул, описывающих мир на субатомном уровне, он постепенно пришел к удивительной по простоте формуле, дающий общее описание эффекта воздействия инструментов измерения на измеряемые объекты микромира, о котором мы только что говорили. В результате им был сформулирован принцип неопределенности, названный теперь его именем: неопределенность значения координаты x неопределенность скорости > h/m, математическое выражение которого называется соотношением неопределенностей Гейзенберга: Δx х Δv > h/m где Δx — неопределенность (погрешность измерения) пространственной координаты микрочастицы, Δv — неопределенность скорости частицы, m — масса частицы, а h — постоянная Планка, названная так в честь немецкого физика Макса Планка, еще одного из основоположников квантовой механики. Постоянная Планка равняется примерно 6,626 x 10–34 Дж·с, то есть содержит 33 нуля до первой значимой цифры после запятой. Термин «неопределенность пространственной координаты» как раз и означает, что мы не знаем точного местоположения частицы. Например, если вы используете глобальную систему рекогносцировки GPS, чтобы определить местоположение этой книги, система вычислит их с точностью до 2-3 метров. (GPS, Global Positioning System — навигационная система, в которой задействованы 24 искусственных спутника Земли. Если у вас, например, на автомобиле установлен приемник GPS, то, принимая сигналы от этих спутников и сопоставляя время их задержки, система определяет ваши географические координаты на Земле с точностью до угловой секунды.) Однако, с точки зрения измерения, проведенного инструментом GPS, книга может с некоторой вероятностью находиться где угодно в пределах указанных системой нескольких квадратных метров. В таком случае мы и говорим о неопределенности пространственных координат объекта (в данном примере, книги). Ситуацию можно улучшить, если взять вместо GPS рулетку — в этом случае мы сможем утверждать, что книга находится, например, в 4 м 11 см от одной стены и в 1м 44 см от другой. Но и здесь мы ограничены в точности измерения минимальным делением шкалы рулетки (пусть это будет даже миллиметр) и погрешностями измерения и самого прибора, — и в самом лучшем случае нам удастся определить пространственное положение объекта с точностью до минимального деления шкалы. Чем более точный прибор мы будем использовать, тем точнее будут полученные нами результаты, тем ниже будет погрешность измерения и тем меньше будет неопределенность. В принципе, в нашем обыденном мире свести неопределенность к нулю и определить точные координаты книги можно. И тут мы подходим к самому принципиальному отличию микромира от нашего повседневного физического мира. В обычном мире, измеряя положение и скорость тела в пространстве, мы на него практически не воздействуем. Таким образом, в идеале мы можем одновременно измерить и скорость, и координаты объекта абсолютно точно (иными словами, с нулевой неопределенностью). В мире квантовых явлений, однако, любое измерение воздействует на систему. Сам факт проведения нами измерения, например, местоположения частицы, приводит к изменению ее скорости, причем непредсказуемому (и наоборот). Вот почему в правой части соотношения Гейзенберга стоит не нулевая, а положительная величина. Чем меньше неопределенность в отношении одной переменной (например, Δx), тем более неопределенной становится другая переменная (Δv), поскольку произведение двух погрешностей в левой части соотношения не может быть меньше константы в правой его части. На самом деле, если нам удастся с нулевой погрешностью (абсолютно точно) определить одну из измеряемых величин, неопределенность другой величины будет равняться бесконечности, и о ней мы не будем знать вообще ничего. Иными словами, если бы нам удалось абсолютно точно установить координаты квантовой частицы, о ее скорости мы не имели бы ни малейшего представления; если бы нам удалось точно зафиксировать скорость частицы, мы бы понятия не имели, где она находится. На практике, конечно, физикам-экспериментаторам всегда приходится искать какой-то компромисс между двумя этими крайностями и подбирать методы измерения, позволяющие с разумной погрешностью судить и о скорости, и о пространственном положении частиц. На самом деле, принцип неопределенности связывает не только пространственные координаты и скорость — на этом примере он просто проявляется нагляднее всего; в равной мере неопределенность связывает и другие пары взаимно увязанных характеристик микрочастиц. Путем аналогичных рассуждений мы приходим к выводу о невозможности безошибочно измерить энергию квантовой системы и определить момент времени, в который она обладает этой энергией. То есть, если мы проводим измерение состояния квантовой системы на предмет определения ее энергии, это измерение займет некоторый отрезок времени — назовем его Δt. За этот промежуток времени энергия системы случайным образом меняется — происходят ее флуктуация, — и выявить ее мы не можем. Обозначим погрешность измерения энергии ΔЕ. Путем рассуждений, аналогичных вышеприведенным, мы придем к аналогичному соотношению для ΔЕ и неопределенности времени, которым квантовая частица этой энергией обладала: ΔЕΔt > h Относительно принципа неопределенности нужно сделать еще два важных замечания: он не подразумевает, что какую-либо одну из двух характеристик частицы — пространственное местоположение или скорость — нельзя измерить сколь угодно точно; принцип неопределенности действует объективно и не зависит от присутствия разумного субъекта, проводящего измерения. Иногда вам могут встретиться утверждения, будто принцип неопределенности подразумевает, что у квантовых частиц отсутствуют определенные пространственные координаты и скорости, или что эти величины абсолютно непознаваемы. Не верьте: как мы только что видели, принцип неопределенности не мешает нам с любой желаемой точностью измерить каждую из этих величин. Он утверждает лишь, что мы не в состоянии достоверно узнать и то, и другое одновременно. И, как и во многом другом, мы вынуждены идти на компромисс. Опять же, писатели-антропософы из числа сторонников концепции «Новой эры» иногда утверждают, что, якобы, поскольку измерения подразумевают присутствие разумного наблюдателя, то, значит, на некоем фундаментальном уровне человеческое сознание связано с Вселенским разумом, и именно эта связь обусловливает принцип неопределенности. Повторим по этому поводу еще раз: ключевым в соотношении Гейзенберга является взаимодействие между частицей-объектом измерения и инструментом измерения, влияющим на его результаты. А тот факт, что при этом присутствует разумный наблюдатель в лице ученого, отношения к делу не имеет; инструмент измерения в любом случае влияет на его результаты, присутствует при этом разумное существо или нет.
|
13.Волновая функция частицы, волны и микрообъекта. Соотношения неопределенностей, их смысл
Экспериментальное
подтверждение идеи де Бройля об
универсальности корпускулярно-волнового
дуализма, ограниченность применения
классической механики к микрообъектам,
диктуемая соотношением неопределенностей,
а также противоречие целого ряда
экспериментов с применяемыми в начале
XX в. теориями привели к новому этапу
развития квантовой теории — созданию
квантовой
механики,
описывающей законы движения и
взаимодействия микрочастиц с учетом
их волновых свойств. Ее создание и
развитие охватывает период с 1900 г.
(формулировка Планком квантовой гипотезы)
до 20-х годов XX в.; оно связано прежде
всего с работами австрийского физика
Э. Шредингера (1887—1961), немецкого физика
В. Гейзенберга и английского физика П.
Дирака (1902—1984).На данном этапе развития
возникли новые принципиальные проблемы,
в частности проблема физической природы
волн де Бройля. Для выяснения этой
проблемы сравним дифракцию световых
волн и микрочастиц. Дифракционная
картина, наблюдаемая для световых волн,
характеризуется тем, что в результате
наложения дифрагирующих волн друг на
друга в различных точках пространства
происходит усиление или ослабление
амплитуды колебаний. Согласно волновым
представлениям о природе света,
интенсивность дифракционной картины
пропорциональна квадрату амплитуды
световой волны. По представлениям
фотонной теории, интенсивность
определяется числом фотонов, попадающих
в данную точку дифракционной картины.
Следовательно, число фотонов в данной
точке дифракционной картины задается
квадратом амплитуды световой волны, в
то время как для одного фотона квадрат
амплитуды определяет вероятность
попадания фотона в ту или иную
точку.Дифракционная картина, наблюдаемая
для микрочастиц, также характеризуется
неодинаковым распределением потоков
микрочастиц, рассеянных или отраженных
по различным направлениям, — в одних
направлениях наблюдается большее число
частиц, чем в других. Наличие максимумов
в дифракционной картине с точки зрения
волновой теории означает, что эти
направления соответствуют наибольшей
интенсивности волн де Бройля. С другой
стороны, интенсивность волн де Бройля
оказывается больше там, где имеется
большее число частиц, т. е. интенсивность
волн де Бройля в данной точке пространства
определяет число частил, попавших в эту
точку. Таким образом, дифракционная
картина для микрочастиц является
проявлением статистической (вероятностной)
закономерности, согласно которой частицы
попадают в те места, где интенсивность
волн де Бройля наибольшая.Необходимость
вероятностного подхода к описанию
микрочастиц является важнейшей
отличительной особенностью квантовой
теории. Можно ли волны де Бройля
истолковывать как волны вероятности,
т. е. считать, что вероятность обнаружить
микрочастицу в различных точках
пространства меняется по волновому
закону? Такое толкование волн де Бройля
уже неверно хотя бы потому, что тогда
вероятность обнаружить частицу в
некоторых точках пространства может
быть отрицательна, что не имеет
смысла.Чтобы устранить эти трудности,
немецкий физик М. Борн (1882—1970) в 1926 г.
предположил, что по волновому закону
меняется не сама вероятность, а величина,
названная амплитудой
вероятности
и обозначаемая
(х, у, z,
t).
Эту величину называют также волновой
функцией
(или функцией).
Амплитуда вероятности может быть
комплексной, и вероятность W
пропорциональна квадрату ее модуля:![]() (216.1)(||2=*,
*
— функция,
комплексно сопряженная с ).
Таким образом, описание состояния
микрообъекта с помощью волновой функции
имеет
статистический, вероятностный
характер:
квадрат модуля волновой функции (квадрат
модуля амплитуды волн де Бройля)
определяет вероятность нахождения
частицы в момент времени t
в области с
координатами х
и x+dx,
у и y+dy,
z
и z+dz.Итак,
в квантовой механике состояние микрочастиц
описывается принципиально по-новому —
с помощью волновой функции, которая
является основным
носителем информации об
их корпускулярных и волновых свойствах.
Вероятность нахождения частицы в
элементе объемом dV
равна
(216.1)(||2=*,
*
— функция,
комплексно сопряженная с ).
Таким образом, описание состояния
микрообъекта с помощью волновой функции
имеет
статистический, вероятностный
характер:
квадрат модуля волновой функции (квадрат
модуля амплитуды волн де Бройля)
определяет вероятность нахождения
частицы в момент времени t
в области с
координатами х
и x+dx,
у и y+dy,
z
и z+dz.Итак,
в квантовой механике состояние микрочастиц
описывается принципиально по-новому —
с помощью волновой функции, которая
является основным
носителем информации об
их корпускулярных и волновых свойствах.
Вероятность нахождения частицы в
элементе объемом dV
равна![]() (216.2)Величина
(216.2)Величина![]() (квадрат
модуля -функции)
имеет смысл
плотности вероятности,
т. е. определяет вероятность нахождения
частицы в единичном объеме в окрестности
точки с координатами х,
у, z.
Таким образом, физический смысл имеет
не сама -функция,
а квадрат ее модуля ||2,
которым задается интенсивность
волн де Бройля.Вероятность
найти частицу в момент времени t
в конечном объеме V,
согласно теореме сложения вероятностей,
равна
(квадрат
модуля -функции)
имеет смысл
плотности вероятности,
т. е. определяет вероятность нахождения
частицы в единичном объеме в окрестности
точки с координатами х,
у, z.
Таким образом, физический смысл имеет
не сама -функция,
а квадрат ее модуля ||2,
которым задается интенсивность
волн де Бройля.Вероятность
найти частицу в момент времени t
в конечном объеме V,
согласно теореме сложения вероятностей,
равна![]() Так
как ||2dV
определяется как вероятность, то
необходимо волновую функцию
нормировать так, чтобы вероятность
достоверного события обращалась в
единицу, если за объем V
принять бесконечный объем всего
пространства. Это означает, что при
данном условии частица должна находиться
где-то в пространстве. Следовательно,
условие нормировки вероятностей
Так
как ||2dV
определяется как вероятность, то
необходимо волновую функцию
нормировать так, чтобы вероятность
достоверного события обращалась в
единицу, если за объем V
принять бесконечный объем всего
пространства. Это означает, что при
данном условии частица должна находиться
где-то в пространстве. Следовательно,
условие нормировки вероятностей![]() (216.3)где данный интеграл (216.3) вычисляется
по всему бесконечному пространству, т.
е. по координатам х,
у, z
от –
до .
Таким образом, условие (216.3) говорит об
объективном существовании частицы в
пространстве.Чтобы волновая функция
являлась объективной характеристикой
состояния микрочастиц, она должна
удовлетворять ряду ограничительных
условий. Функция ,
характеризующая вероятность
обнаружения действия микрочастицы в
элементе объема, должна быть конечной
(вероятность не может быть больше
единицы), однозначной
(вероятность
не может быть неоднозначной величиной)
и непрерывной
(вероятность не может изменяться
скачком).Волновая функция удовлетворяет
принципу суперпозиции:
если система может находиться в различных
состояниях, описываемых волновыми
функциями 1,
2,...,
n,...
то она также может находиться в состоянии
,
описываемом линейной комбинацией этих
функций:
(216.3)где данный интеграл (216.3) вычисляется
по всему бесконечному пространству, т.
е. по координатам х,
у, z
от –
до .
Таким образом, условие (216.3) говорит об
объективном существовании частицы в
пространстве.Чтобы волновая функция
являлась объективной характеристикой
состояния микрочастиц, она должна
удовлетворять ряду ограничительных
условий. Функция ,
характеризующая вероятность
обнаружения действия микрочастицы в
элементе объема, должна быть конечной
(вероятность не может быть больше
единицы), однозначной
(вероятность
не может быть неоднозначной величиной)
и непрерывной
(вероятность не может изменяться
скачком).Волновая функция удовлетворяет
принципу суперпозиции:
если система может находиться в различных
состояниях, описываемых волновыми
функциями 1,
2,...,
n,...
то она также может находиться в состоянии
,
описываемом линейной комбинацией этих
функций:![]() где
Сn
(n=1,
2, ...) — произвольные, вообще говоря,
комплексные числа. Сложение волновых
функций
(амплитуд вероятностей), а не вероятностей
(определяемых квадратами модулей
волновых функций) принципиально отличает
квантовую теорию от классической
статистической теории, в которой для
независимых событий справедлива теорема
сложения вероятностей.Волновая
функция ,
являясь основной характеристикой
состояния микрообъектов, позволяет в
квантовой механике вычислять средние
значения физических величин, характеризующих
данный микрообъект. Например, среднее
расстояние r
электрона от ядра вычисляют по формуле
где
Сn
(n=1,
2, ...) — произвольные, вообще говоря,
комплексные числа. Сложение волновых
функций
(амплитуд вероятностей), а не вероятностей
(определяемых квадратами модулей
волновых функций) принципиально отличает
квантовую теорию от классической
статистической теории, в которой для
независимых событий справедлива теорема
сложения вероятностей.Волновая
функция ,
являясь основной характеристикой
состояния микрообъектов, позволяет в
квантовой механике вычислять средние
значения физических величин, характеризующих
данный микрообъект. Например, среднее
расстояние r
электрона от ядра вычисляют по формуле![]()

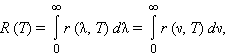
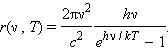
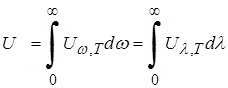 .
(1)
.
(1)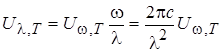 .
.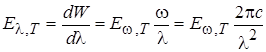 ,
(2)
,
(2)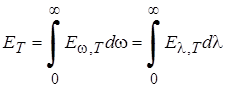 .
(3)
.
(3)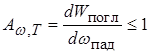 .
.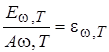 .
(4)
.
(4)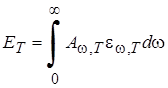 .
.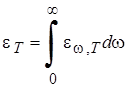
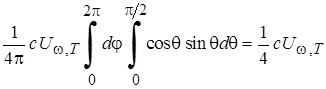 .
.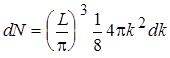 .
.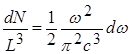 .
.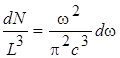 .
.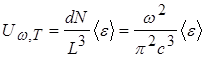 .
(9)
.
(9)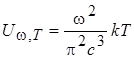 .
(10)
.
(10) .
.