Билет 43. В основу вывода расчет¬ных формул для червячных передач положены те же исходные зависимости и предположения, что и в зубчатых передачах. Формула проверочного расчета червяч¬ных передач по контактным напряжениям:

(2.5.18)

где   - расчетное контактное напряжение для поверхностей зубьев и витков в зоне зацепления, Н/мм2,  d1 , d2 - диаметры червяка и колеса, мм;   - окружная сила на червячном коле¬се, Н, - коэффициент нагрузки, учитывающий неравномерность распределения нагрузки вследствие деформации деталей и дополнительные динамические нагрузки (при окружной скорости червячного колеса   - К= 1, при   - К= 1,1…1,3). Червячные передачи работают плавно, бесшумно, поэтому в них дополнительные динамические нагрузки невелики. Хорошая приработка зубьев колес к виткам червяков значительно умень¬шает концентрацию нагрузки.

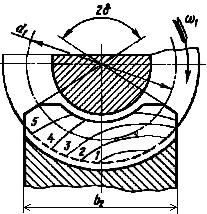Рисунок 2.5.13 Схема расположения контактных линий (1...5) в процессе зацепления червячной пары.

Если в формуле для расчета контактных напряжений (2.5.18) подставить значения d1=gm , d2=mz2 ,   , q  , К=1, то получим формулу проектировочного расчета червячных передач:

(2.5.19)

где  - межосевое расстояние в мм,  Т2 - вращающий момент на червячном колесе в Н мм. Если червячная передача должна быть стандартной, то полу¬ченное расчетным путем значение округляют в большую сторо¬ну до стандартного значения, которому соответству¬ют определенные m, q, z1 , z2. Для нестандартных червячных передач полученное значение округляют до ближайшего значения из ряда нормальных линейных размеров.

Билет 44.

Расчет зубьев червячного колеса на изгиб аналогичен расчету зубьев цилиндрических косозубых колес. Вследствие дугообразной формы зубьев считают, что их прочность на изгиб примерно на 40 % выше, чем зубьев цилиндрических косозубых колес. Формула проверочного расчета зубьев червячного колеса имеет вид:

(2.5.20)

где  - расчетное напряжение изгиба в опасном сечении зубьев червячного колеса; < img src="../img/442.JPG"> - коэффициент формы зуба колеса, который выбирают в зависимости от эквивалентного числа зубьев   , где   - делительный угол подъема линии витка. Витки червяка на изгиб как правило не проверяются, так как они более прочны, чем зубья колеса.

Билет 45.

При работе червячных передач выделяется большое количе¬ство теплоты. Потерянная мощность Р1 на трение в зацеп¬лении и подшипниках, а также на размешивание и разбрызгива¬ние масла переходит в теплоту, которая нагревает масло, а оно через стенки корпуса передает эту теплоту окружающей среде. Если отвод теплоты недостаточен, передача перегреется. При перегреве смазочные свойства масла резко ухудшаются (его вязкость падает) и возникает опасность заедания, что может привести к выходу передачи из строя. Поэтому червячные передачи во избежание их перегрева предпочти¬тельно использовать в приводах периодического (а не непрерыв¬ного) действия. Тепловой расчет червячной передачи производится как проверочный после определения размеров корпуса при эскизном проектировании. Тепловой расчет червячной передачи при установившемся режиме работы производится на основе теплового баланса, т. е. равенства тепловыделения Qв и теплоотдачи Qo:

(2.5.21)

Количество теплоты, выделяющееся в непрерывно работаю¬щей передаче в одну секундy  (2.5.22), где A— площадь поверхности корпуса, омываемая внутри мас¬лом или его брызгами, а снаружи воздухом, м2. Поверхность днища корпуса не учитывается, так как она не омывается свобод¬но циркулирующим воздухом;  tВ— температура воздуха вне кор¬пуса; в цеховых условиях обычно tВ = 20°С;  tм—температура масла в корпусе передачи, °С;  Кm— коэффициент теплопередачи, т. е. число, показывающее, сколько теплоты в секунду передается одним квадратным метром поверхности корпуса при перепаде температур в один градус, зависит от материала корпуса ре¬дуктора и скорости циркуляции воздуха (интенсивности вентиля¬ции помещения). Для чугунных корпусов, не обдуваемых вентилятором, прини¬мают КТ= 12... 18 Вт/(м2-°С). Большие значения используют при незначительной шероховатости и загрязненности поверхности наружных стенок, хорошей циркуляции воздуха вокруг корпуса и интенсивном перемешивании масла (при нижнем расположении червяка).  Температура масла в корпусе червячной передачи при непрерывной работе без искусственного охлаждения

(2.5.23)

Если при расчете температура масла окажется больше допускаемой, то либо увеличивают поверхность охлаждения, применяя охлаждающие ребра, либо применяют искусственное охлаждение (обдувают корпус или охлаждают масло), способы охлаждения:

·     дополнительным оребрением и обдувом корпуса вентилятором. При этом k_T = 20…28 Вт/ (м² × °С).

·     устраивают в корпусе водяные полости или змеевики с проточной водой. При этом k_T повышается до 90…200 Вт/ (м² × °C) при скорости воды в трубе до 1 м/с.

·     применяют циркуляционные системы смазки со специальными холодильниками.

Билет 46.

Валы и оси. Расчетные схемы. Критерии работоспособности и расчета.

Зубчатые колеса, шкивы, звездочки и другие вращающиеся детали машин устанавливают на валах или осях. Вал – деталь машин, предназначенная для поддержания сидящих на нем деталей и передачи крутящего момента. При работе вал испытывает деформации кручения и изгиба, иногда – растяжения-сжатия. Ось – деталь машин и механизмов, служащая для поддержания вращающихся частей, но не передающая полезный крутящий момент, а, следовательно, не испытывает кручения.

Расчёты валов и осей

Основным критерием работоспособности валов и осей являются сопротивление усталости материала и жёсткость. Расчёт валов выполняется в два этапа: предварительный (проектный) и окончательный (проверочный).  Проектировочный расчёт вала выполняют как условный расчёт только на кручение для ориентировочного определения посадочных диаметров. Исходя из условия прочности на кручение 

получим формулу проектировочного расчёта

где М_k – крутящий момент в расчётном сечении, Н*м;  Н/мм2 – допускаемое напряжение при кручении Проверочный расчет для валов - расчёт на сопротивление усталости - является основным расчётом на прочность. Основными нагрузками на валы являются силы от передач через насаженные на них детали: зубчатые или червячные колёса, звёздочки, шкивы. Проверочный расчет вала производится с применением гипотез прочности.Условие прочности в этом случае имеет вид:

где М_экв — так называемый эквивалентный момент. При гипотезе наибольших касательных напряжений (иначе — тре¬тья гипотеза)

При гипотезе потенциальной энергии формоизменения (иначе — пятая гипотеза)

где в обеих формулах М_к и М„ — соответственно крутящий и суммарный изгибающий моменты в рассматриваемом сечении вала. Числовое зна¬чение суммарного изгибающего момента равно геометрической сумме изгибающих моментов, возникающих в данном сечении от вертикально и горизонтально действующих внешних сил, т. е.

При проектировочном расчёте оси ее рассматривают как балку, свободно лежащую на опорах и нагруженную сосредоточенными словами, вызывающими изгиб. Устанавливают опасное сечение, для которого требуемый диаметр оси определяют из условия прочности на изгиб 

откуда  где М_и – максимальный изгибающий момент, Н*м;  - допускаемое напряжение изгиба, Н/мм2. Выбор допускаемых напряжений  . Оси изготовляемые из среднеуглеродистых сталей Во вращающихся осях Проверочный расчёт осей - частный случай расчёта валов при крутящем моменте М_к = 0. 

Алгоритм проверочного расчета вала

1. Привести действующие на вал нагрузки к его оси, освободить вал от опор, заменив их действие реакциями в вертикальной и горизонтальной плоскостях. 2. По заданной мощности Р и угловой скорости ? определить вращающие моменты, действующие на вал. 3. Вычислить нагрузки F₁, Fr₁, F₂, F_r2, приложенные к валу. 4. Составить уравнения равновесия всех сил, действующих на вал, отдельно в вертикальной плоскости и отдельно в горизонтальной плос¬кости и определить реакции опор в обеих плоскостях 5. Построить эпюру крутящих моментов. 6. Построить эпюры изгибающих моментов в вертикальной и гори¬зонтальной плоскостях (эпюры M_x и М_y). 7. Определить наибольшее значение эквивалентного момента (3.1.4), (3.1.5),:

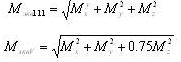
8. Положив  _экв = [ ], определить требуемый осевой момент сопро¬тивления: Wx = М_экв/[ ] Учитывая, что для сплошного круглого сечения

определяем d по следующей формуле: 

Расчетные схемы Расчетные схемы валов и осей изображают в виде балок на шарнирных опорах, которые нагружены поперечными и осевыми силами, возникающие в зацеплении установленных на них зубчатых колес, от натяжения ветвей ременной или цепной передачи, от действия собственного веса шкивов, барабанов и других установленных на валу деталей. При составлении расчетных схем валов и осей необходимо с некоторым приближением определить расстояние между опорами, места размещения деталей, через которые передаются на валы и оси внешние нагрузки. При коротких опорах вала или оси (подшипники качения, подшипники скольжения с отношением длины цапфы к ее диаметру l / d <0,6) центр опоры совмещают с серединой подшипника (рис. 31.7, а). При длинных опорах скольжения (l / d> 0,6) вследствие неравномерности распределения нагрузки по длине подшипника теоретически центр опоры считают расположенным примерно в (0,25 ... 0,30) / от края подшипника со стороны нагруженной части вала или оси (рис. 31.7, б). Валы, которые передают нагрузку от насаженных на него деталей, передающих нагрузку в среднем сечении по длине посадочной поверхности. Это предположение можно брать, если расстояние между опорами вала или оси значительно превышает ширину Ь детали. В противном случае следует учитывать закономерность распределения нагрузки вдоль посадочной поверхности хотя бы разнесением внешней нагрузки F, как показано на рис. 31.7, в. Расчетные схемы валов и осей могут быть чрезвычайно разнообразными. Объектом нашего изучения будут двухопорных валы и оси как статически определенные системы. Собственный вес валов и установленных на них деталей преимущественно в расчетах не учитывают при небольших их размерах, хотя ее учета не создает принципиальных трудностей. Расчетные схемы промежуточных валов многоступенчатых зубчатых передач изображены на рис. г, д, е. Эти схемы отличаются между собой взаимным расположением мест приложения сил, возникающих в зацеплении зубчатых колес, расположенных на валу. При анализе таких схем погрузки валов следует рассматривать отдельно силовые факторы в разных плоскостях, а затем грустить геометрическое. Из рассмотренных схем видно, что валы в процессе работы испытывают деформаций изгиба, растяжения или сжатия и кручения. Постоянство направления поперечных относительно продольной оси вала сил вызывает в валах, вращающихся появление циклически переменных напряжений изгиба, а действие осевых сил - возникновение в сечениях валов напряжений растяжения или сжатия. Характер изменения касательных напряжений кручения соответствует характеру изменения во времени крутящего момента Т. Таким образом, различные сечения валов находятся под действием переменных во времени нормальных и касательных напряжений. Поэтому для большинства валов современных быстроходных машин такой критерий прочности, как устойчивость валов против усталостного разрушения, имеет решающее значение. Усталостное разрушение происходит в 40-50% случаев выхода валов из строя. Для тихоходных валов или валов, подверженных действию кратковременных пиковых перегрузок, основным расчетным критерием является также статическая прочность. Валы, имеющие значительные (по сравнению с диаметром) расстояния между опорами, могут быть недостаточно жесткими в поперечном направлении. Это может вызвать нарушение геометрии зацеплений зубчатых колес, заклинивания валов в опорах или недопустимы поперечные колебания валов. Поэтому важным критерием расчета длинных валов также условие достаточной жесткости

Критерии работоспособности и расчета

1)Валы и вращающиеся оси при работе испытывают циклически изменяющиеся напряжения. Основным критерием их работоспособности являются сопротивление усталости и жесткость. Сопротивление усталости оценивается коэффициентом запаса прочности, а жесткость – прогибом в местах посадки деталей и углами закручивания сечений. Практикой установлено, что основной вид разрушения валов и осей быстроходных машин носит усталостный характер. Расчетными силовыми факторами являются крутящие и изгибающие моменты.

2)Валы и оси следует конструировать по возможности гладкими с минимальным числом уступов. Каждая насаживаемая на вал или ось деталь должна свободно проходить до своей посадочной поверхности. Торцы валов и осей и их уступы выполняют с фасками (рис.3.1.2, 3.1.4) для удобства насадки деталей. Для увеличения изгибной жесткости валов и осей насаживаемые детали располагают ближе к опорам. Для повышения несущей способности валов и осей их поверхность подвергают упрочнению.

Билет 47.

Расчет валов и осей на прочность и выносливость

РАСЧЕТ НА ПРОЧНОСТЬ

При расчете валов на жесткость диамет­ры их получаются больше, чем при расчете на прочность, и они работают преимущест­венно с невысокими напряжениями. По­этому расчет валов целесообразно вести упрощенно, не учитывая динамический характер нагрузки, т. е. не вводя в формулы коэффициенты концентрации напряжений, характеристики циклов нагружения и т.п. Эти факторы учитывают приближенно со­ответствующим выбором допускаемых на­пряжений.

Валы на прочность рассчитывают по формул:

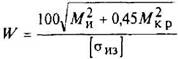
или

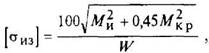
где W - момент сопротивления в опасном сечении, мм³: W = πd³/32 ≈ 0,1d³ – для круглого сплошного сечения (см. рис. 1); W = πd³/32(l – d₀⁴/d⁴) ≈ 0,1(d⁴-d₀⁴)/d - для круглого полого сечения (см. рис. 2); [σ_из] - допускаемое напряжение, МПа (см. табл. 9), определяемое при динамическом расче­те стальных валов по пределу выносливости с учетом факторов, вызывающих концен­трацию напряжений, и диаметру вала; М_и -максимальный изгибающий момент в опасном сечении, Н мм:

здесь М_и.г и М_и.в - максимальные изгибаю­щие моменты в опасном сечении, Н·мм, действующие соответственно в горизон­тальной и вертикальной плоскостях; М_кр -максимальный крутящий момент в опасном сечении, Н·мм;

- максимальный приведенный (резуль­тирующий) момент в опасном сечении, Н · мм.

Диаметр вала из среднеуглеродистой стали (σ_в = 500 … 800МПа) при расчете на прочность приближенно определяют по следующим формулам:

при постоянной нагрузке и небольших изгибающих моментах (короткие валы из стали Ст5, Ст6 и 45)

при переменной нагрузке и малых изги­бающих моментах или при постоянной нагрузке и средних изгибающих моментах

при переменной нагрузке и средних изгибающих моментах или при постоянной нагрузке и значительных изгибающих мо­ментах (длинные валы)

где d - в см; Р - передаваемая мощность, кВт; n - частота вращения вала, мин^-1.

Формулы составлены из расчета вала на кручение и обусловливают напряжения: формула (1) τ_кр = 50МПа; формула (2) τ_кр = 37МПа; формула (3) τ_кр = 28,5МПа. При наличии шпоночного паза в опасном сечении вала полученное значение необхо­димо увеличить на 5-10%.

Расчет на выносливость

Для расчета валов на выносливость необходимо знать их конструкцию и размеры. Поэтому при проектировании валов для предварительного определения размеров их рассчитывают на статическую прочность, а затем окончательно на выносливость. Основной расчетной нагрузкой являются крутящий момент Т и изгибающий момент М. Влияние сжимающих или растягивающих сил обычно мало и поэтому не учитывается. Расчет осей является частным случаем расчета валов при Т = 0. Перед началом расчета обычно известны крутящий момент Т или мощность Р и частота вращения п, нагрузка и размеры основных деталей, расположенных на валу (например, зубчатых колес). Требуется выбрать материал и размеры вала. На практике обычно используют следующий порядок проектного расчета вала:

1. Предварительно определяют наибольший диаметр вала (d) из расчета на кручение при пониженных допускаемых касательных напряжениях (изгибающий момент пока не известен, так как неизвестно расположение опор и места приложения нагрузок). Напряжения кручения

 или  . (13.1)

Обычно принимают для редукторных валов

= (15...20)МПа. (13.2)

Выбрать диаметр проектируемого вала можно, также ориентируясь на известный диаметр того вала, с которым он соединяется (если валы передают одинаковый момент Т, то и диаметры могут быть одинаковые). Например, если вал соединяется с валом электродвигателя (или другой машины), то диаметр его входного конца можно принять равным или близким к диаметру выходного конца вала электродвигателя.

2. После определения диаметра вала [на рис. 13.1 под шестерней из расчета по формуле (13.1)] и выходного конца по диаметру вала электродвигателя разрабатывают его конструкцию.

3. Выполняют уточненный расчет валов полученной конструкции на сопротивление усталости и если необходимо, вносят изменения. При этом учитывают, что диаметр вала является одним из основных параметров, определяющих размеры и нагрузочную способность подшипников. На практике иногда диаметр вала определяется не прочностью самого вала, а прочностью подшипников. Поэтому расчеты вала и подшипников взаимосвязаны.

Билет 48.

Расчет на жесткость