ВСМ_ЛАБ_4 / ВСМ_ЛАБ_4

Санкт-Петербургский Государственный Электротехнический Университет «ЛЭТИ»

Кафедра ИИСТ

Лабораторная работа № 4

"Нахождение уравнений регрессии, коэффициента линейной корреляции и интервальной оценки коэффициента корреляции двух случайных величин"

Факультет:

Группа:

Студент:

Преподаватель: Орлова Н.В.

Санкт-Петербург.

2013

Цель работы: по результатам измерений двух СВ X и Y построить поле корреляции, определить и построить линейные уравнения регрессии. Определить коэффициент корреляции между результатами измерений двух случайных величин X и Υ и дать интервальную оценку коэффициента корреляции.

Значения СВ X и Y:

X = [-0.18 1.9 0.16 0.73 1.10 1.04 -0.42 -1.75 1.49 1.3];

Y = [0.96;0.95;-0.48;0.01;2.02;0.24;0.78;2.55;2.33;0.46];

График:

α = 16˚C , β = 36˚C

Результаты, полученные в MathLab:

Коэффициент корреляции:

rxy = 0.4684

0,4< rxy < 0.7 – Средняя корреляция

Оценка по графику коэффициента корреляции, как:

α – угол наклона линии регрессии Y к оси х, β – угол наклона линии регрессии Х к оси у.

rxy = = 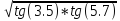2,596

Значение коэффициента корреляции rxy, полученного при выполнении программы не совпадают со значениями, полученными по графику.

Расчет доверительного интервала коэффициента корреляции rxy с

помощью формулы Фишера:

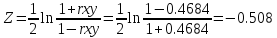
Доверительный интеграл может быть определен как:

где σz = - СКО

а квантили находятся из таблицы нормальной функции распределения на уровне вероятности p:

Таким образом, доверительный интервал для коэффициента корреляции:

Z_min = Z-σz* U_p = - 0,378*0,47=-0,68566

Z_min = Z+σz* U_p = +0,378*0,47=-0,33034

-0,33034≤ Z ≤ -0,68566