
- •16. Теорема об эквивалентности двух пар сил, расположенных в одной плоскости .И о перемещении пары сил в плоскость параллельную плоскости её действия
- •18Сложение пар сил. Условия равновесия системы пар сил
- •29,Векторные и аналитические условия равновесия произвольной пространственной системы сил
- •1. Скорость и ускорение точки в полярных координатах
- •Вращение твёрдого тела вокруг неподвижной оси
- •Ускорение точки
- •Векторные скорости и ускорения точек тела
- •Уравнения плоского движения твердого тела
- •Угловая скорость и угловое ускорение тела при плоском движении.
- •Мгновенный центр скоростей
- •Методы нахождения положения мцс
Уравнения плоского движения твердого тела
Для
задания положения плоской фигуры на
плоскости относительно системы координат
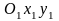 ,
лежащей в плоскости фигуры, достаточно
задать на этой плоскости положение
отрезка АВ, скрепленного с фигурой.
,
лежащей в плоскости фигуры, достаточно
задать на этой плоскости положение
отрезка АВ, скрепленного с фигурой.
Положение
отрезка АВ, относительно системы
координат
определяется
заданием координат какой-нибудь точки
этого отрезка и его направления.
Например, координаты точки А (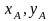 )
и направление, заданное углом
.
)
и направление, заданное углом
.
Уравнения
движения плоской фигуры относительно
системы координат
имеют вид: 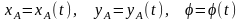 .
.
Т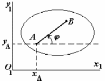 вердое
тело при плоском движении имеет три
степени свободы.
вердое
тело при плоском движении имеет три
степени свободы.
Функции
называются уравнениями плоского движения твердого тела.
Рис. 6-2
П ерейдем
к изучению движения отдельной точки
твердого тела. Положение любой точки
М плоской фигуры относительно подвижной
системы отсчета
ерейдем
к изучению движения отдельной точки
твердого тела. Положение любой точки
М плоской фигуры относительно подвижной
системы отсчета
 ,
скрепленной
с этой движущейся фигурой и лежащей в
ее плоскости, полностью определяется
заданием координат x и y точки М
(Рис.6-3).
,
скрепленной
с этой движущейся фигурой и лежащей в
ее плоскости, полностью определяется
заданием координат x и y точки М
(Рис.6-3).
Рис. 6-3
Между координатами точки М в различных системах отсчета существует связь:
 , (6-1)
, (6-1)
где
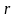 - длина отрезка ОМ,
- длина отрезка ОМ,
 - постоянный угол между ОМ и осью
- постоянный угол между ОМ и осью
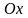 .
С учетом выражений
.
С учетом выражений
 и
и  получаем
получаем
 ,
(6-2)
,
(6-2)
Формулы (6-2) являются уравнениями движения точки М плоской фигуры относительно координат . Эти формулы позволяют определить координаты любой точки плоской фигуры по заданным уравнениям движения этой фигуры и координатам этой точки относительно подвижной системы отсчета, скрепленной с движущейся фигурой.
Используя матрично-векторные обозначения уравнения (6-2) можно записать в такой форме:
 , (6-3)
, (6-3)
где А – матрица поворота на плоскости:
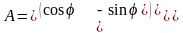 ,
,  ,
,  ,
, 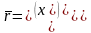 .
.
10. Теорема о перемещении плоской фигуры в её плоскости. Следствия из теоремы .
11. Доказательства независимой угловой скорости и углового ускорения плоской фигуры от выбора полюса
Угловая скорость и угловое ускорение тела при плоском движении.
Для характеристики вращательной части плоского движения твердого тела вокруг подвижной оси, проходящей через выбранный полюс, вводится понятие угловой скорости и углового ускорения .
и , где - единичный вектор, направленный по оси вращения.
Если
угол поворота вокруг подвижной оси,
проходящей через полюс, обозначить
,
то
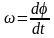 ,
а
,
а

Векторы и можно изображать в любых точках подвижной оси вращения, т.е. они являются свободными векторами.
12. Теорема о сложении скоростей точки плоской фигуры. Следствия из теоремы.
13.Мгновенный центр скоростей плоской фигуры. Теорема о существовании МЦС.
Мгновенный центр скоростей
Мгновенным центром скоростей называется точка плоской фигуры, скорость которой в данный момент времени равна нулю.
Теорема.
В каждый момент времени при плоском
движении фигуры в ее плоскости при
 (непоступательное движение), имеется
один единственный центр скоростей.
(непоступательное движение), имеется
один единственный центр скоростей.
Д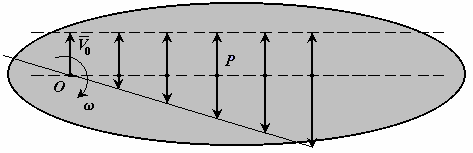 ля
доказательства достаточно указать
способ нахождения мгновенного центра
скоростей, если известны скорость
какой-либо точки О плоской фигуры и ее
угловая скорость в рассматриваемый
момент времени.
ля
доказательства достаточно указать
способ нахождения мгновенного центра
скоростей, если известны скорость
какой-либо точки О плоской фигуры и ее
угловая скорость в рассматриваемый
момент времени.
Рис. 6-6
 ,
, 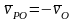 ,
, 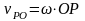 ,
следовательно
,
следовательно
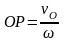 .
.
Мгновенный
центр скоростей находится на перпендикуляре
к скорости
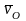 ,
проведенном из точки О, на расстоянии
,
проведенном из точки О, на расстоянии
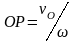 .
.
Мгновенный центр скоростей это единственная точка плоской фигуры для данного момента времени. В другой момент времени мгновенным центром скоростей будет уже другая точка.
Возьмем
точку Р за полюс
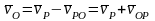
Так
как
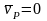 ,
то
,
то
 .
Аналогичный результат получается для
любой другой точки плоской фигуры.
.
Аналогичный результат получается для
любой другой точки плоской фигуры.
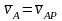
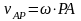
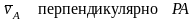 .
.

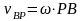
 .
.
Скорости точек плоской фигуры определяются в данный момент так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей.
Скорости точек плоской фигуры пропорциональны их расстояниям до мгновенного центра скоростей.
14. Способы определения МЦС плоской фигуры.
Методы нахождения положения МЦС
1).
Известен вектор скорости
|
|
МЦС
(точка P) находится на перпендикуляре
к вектору
,
проведенном через точку A. Расстояние
|
|
2).
Известны не параллельные друг другу
скорости
и
|
|
МЦС
(точка P) находится в точке пересечения
перпендикуляров, проведенных через
точки A и B к скоростям этих точек.
Угловая скорость плоской фигуры равна
|
|
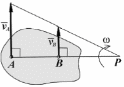
3).
Известны параллельные друг другу
скорости
и
точек A и B плоской фигуры, перпендикулярные
отрезку AB, направленные в одну сторону
и не равные по модулю
( |
|
МЦС
(точка P) находится в точке пересечения
продолжения отрезка AB
и прямой,
проведенной через концы векторов
и
.
При заданной длине отрезка AB
расстояния
от МЦС до точек A
и B
определяются
из пропорции
|
|

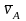 какой -либо точки A плоской фигуры и
ее угловая скорость
.
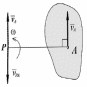
какой -либо точки A плоской фигуры и
ее угловая скорость
.
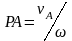 и откладывается в сторону, которую
указывает вектор
после
поворота на угол
и откладывается в сторону, которую
указывает вектор
после
поворота на угол
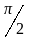 в направлении дуговой стрелки
в направлении дуговой стрелки
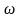 .
При этом получается, что скорость
.
При этом получается, что скорость (
(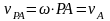 )
)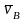 двух точек плоской фигуры.
двух точек плоской фигуры.
 .
Отметим, что для нахождения только
положения МЦС достаточно знать лишь
направления
скоростей двух точек .
.
Отметим, что для нахождения только
положения МЦС достаточно знать лишь
направления
скоростей двух точек .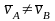 ).
).
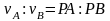 .
Угловая
скорость фигуры
.
Случай равенства (
.
Угловая
скорость фигуры
.
Случай равенства ( )
см. п. 6.
)
см. п. 6.