1.В современных условиях, когда наука и техника стремительно развиваются, специальные знания быстро устаревают. Поэтому для решения принципиально новых задач специалисты должны обладать знаниями в области фундаментальных наук.

Как фундаментальная наука, теоретическая, общая, или классическая механика, была и остается одной из наук, формирующих у специалиста научное мировоззрение и углубленные знания о природе. Она служит для воспитания творческих навыков применения универсальных методов теоретической механики к построению моделей самых различных явлений в природе и технике и развитию творческого, научного мышления.

2. История развития и становления теоретической механики – это отдельный предмет. Краткие сведения о наиболее значительных научных достижениях учёных-механиков можно найти в литературном источнике [1]. Основательное же его изучение рекомендуем начинать (после освоения данного «Курса») с литературы [2-7]. Здесь ограничимся лишь перечислением основных периодов развития механики:

1. Донаучный – заканчивается 4-м веком до н.э.; характеризуется живым созерцанием и накоплением материала, который ещё не подвергается существенной абстрактно-теоретической обработке;

2. Элементарный период – заканчивается серединой 17-го столетия; характеризуется рассмотрением простых видов механического движения, слабыми методами исследования и наличием несовершенных теорий («слабыми» и «несовершенными» с позиций сегодняшнего дня);

3. Период формирования современных понятий и формулировок законов – заканчивается 30-ми годами 18-го столетия; характеризуется созданием мощных методов исследования (дифференциального и интегрального исчислений) и построением совершенных теорий;

4. Период триумфального шествия теорий механического движения и преувеличения их значимости в вопросах познания окружающего мира - 18-19 века. В этот исторический период открытия одно за другим «сходят с кончика пера». Характерным в этом смысле является пример предсказания и обнаружения планеты Нептун. Научные успехи в вопросах механики приводят к широкому распространению в обществе ложной точки зрения, заключающейся в том, что все природные явления можно объяснить с позиций законов механического движения. Такая система взглядов, во многом оказавшая отрицательное влияние на развитие науки вообще, получила название «механицизм».

5. Период формирования теоретических основ различных прикладных вопросов механики –– появляются теория механизмов и машин, теория уравновешивания роторов, теория колебаний, теория устойчивости, теория гироскопов, ракетодинамика, механика сплошной среды, робототехника и другие. Заканчивается примерно 1970-м годом.

6. Современный период – характеризуется появлением мощного метода исследований с помощью компьютерной техники, позволившей существенно расширить классы решаемых практических задач.

3. Основные понятия и определения статики. Задачи статики.

Статика – это раздел теоретической механики, в котором изучают условия равновесия системы сил, приложенных к твердому телу, а также приведение сложной системы сил к простейшему виду.

Материальной точной называют простейшую модель материального тела, размерами которого пренебрегают, и обладающую некоторой массой.

Механической системой называют совокупность материальных точек, связанных и взаимодействующих между собой.

Абсолютно твердым телом называют механическую систему, расстояния между точками которой не изменяются при любых взаимодействиях.

Сила – мера механического взаимодействия материальных тел, в результате которого тела могут сообщать друг другу ускорения и деформироваться.

Система сил – это совокупность нескольких сил, действующих на данное тело или систему тел.

Эквивалентные системы сил – это такие системы сил, действие которых на одно и то же тело одинаково при прочих равных условиях.

Равнодействующей данной системы сил называют силу, действие которой на тело или материальную точку эквивалентно действию этой системы сил.

Уравновешенной системой сил называют систему сил, действие которой на твердое тело, находящееся в покое или движущееся по инерции, не приводит к изменению его состояния.

Уравновешивающей силой заданной системы сил называют такую силу, которая будучи присоединенной к этой системе сил, составит вместе с ней новую систему сил, эквивалентную нулю.

Сосредоточенной силой называют силу, приложенную к какой-либо точке твердого тела. Распределенными называют силы, действующие на все точки данного объема или данной части поверхности, или линии.

Внутренними силами называют силы взаимодействия между телами, входящими в механическую систему.

Внешними силами называют силы, с которыми на тела рассматриваемой механической системы действуют тела, не входящие в данную механическую систему.

Основные учебные задачи статики – изучение законов и методов, с помощью которых можно: 1) определять действующие на тела неизвестные силы; 2) преобразовывать одни системы сил в другие.

4.Аксиомы статики. Типы связей и их реакции. Реакция жесткой заделки.

1)Аксиома о равновесии системы двух сил. Две силы, приложенные к абсолютно твердому телу, будут уравновешены (эквивалентны нулю), если равны по модулю и действуют по одной прямой в противоположных направлениях.

2) аксиома о добавлении (отбрасывании) системы сил, эквивалентной нулю.

Не нарушая состояние абсолютно твердого тела, к нему можно приложить или отбросить уравновешенную систему сил.

Следствие. Не нарушая состояние твердого тела, силу можно переносить по линии ее действия, т.е. сила, приложенная к абсолютно твердому телу, является скользящим вектором.

3) Аксиома параллелограмма сил.

Не нарушая состояние твердого тела, две силы, приложенные в одной его точке, можно заменить равнодействующей, равной их геометрической сумме и приложенной в той же точке. Справедливо и обратное: одну силу, приняв ее за равнодействующую можно разложить на две составляющие силы.

4) Аксиома о равенстве сил действия и противодействия.

Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны (по третьему закону Ньютона). Силами взаимодействия являются силы действия и силы противодействия.

5) Аксиома затвердения.

Равновесие деформируемого тела не нарушиться, если тело считать абсолютно твердым.

6) Аксиома связей.

Всякое несвободное тело можно сделать свободным, елси отбросить наложенные на него связи и заменить их силами – реакциями связи.

Типы связей и их реакции:

а) опора на идеально гладкую поверхность – реакция поверхности направлена по нормали к ней, т.е. перпендикулярно касательной – нормальная реакция;

б) одна из соприкасающихся поверхностей является точкой (угол), реакция направлена по нормали к другой поверхности;

в) нить – реакция направлена вдоль нити к точке подвеса;

г) цилиндрический шарнир (шарнирно-неподвижная опора) – реакция может иметь любое направление в плоскости. При решении задач заменяется двумя взаимно перпендикулярными составляющими;

д) цилиндрическая шарнирно-подвижная опора (шарнир на катках) – реакция направлена перпендикулярно опорной плоскости;

е) сферический (шаровой) шарнир – реакция может иметь любое направление в пространстве. При решении задач заменяется тремя взаимно перпендикулярными составляющими;

ж) невесомый стержень (обязательно невесомый) – реакция направлена вдоль стержня;

з ) "глухая" заделка (вмурованная балка) – возникает произвольно направленная реакция – сила и реактивный момент, также неизвестный по направлению. Реакция раскладывается на две составляющие.

5.Аналитический и геометрические способы определения равнодействующей системы сходящихся сил.

Геометрически: Нахождение равнодействующей основано на построении векторного многоугольника сил, который называют силовым многоугольником. Равнодействующая в силовом многоугольнике соединяет начало первой силы с концом последней.

Строить многоугольник сил можно в любой последовательности, от которой меняется лишь форма многоугольника, а равнодействующая остается неизменной. Для пространственной системы сил многоугольник является пространственной фигурой, для плоской – плоской фигурой.

Если многоугольник строить в масштабе, то величину равнодействующей можно найти непосредственной измерением ее.

Аналитически: Равнодействующую системы сходящихся сил можно определить аналитическим способом, который основан на проектировании сил системы и равнодействующей на выбранные оси координат, начало которых находиться обычно в точке схода сил:

, где – проекции равнодействующей на соответствующие оси координат).

Модуль равнодействующей: .

6.Геометрические и аналитические условия равновесия системы сходящихся сил. Теорема о равновесии трех сил.

Для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая была равна нулю:

Геометрически условие равновесия означает, что силовой многоугольник будет замкнутым, т.е. при построении силового многоугольника конец последнего вектора совпадает с началом первого вектора.

Аналитически для равновесия системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил системы на соответствующие координатные оси равнялось нулю:

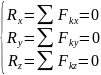- аналитическое условие равновесия.

Для плоской системы сходящихся сил будет достаточно двух уравнений.

7.Проекция силы на ось и на плоскость.

Проекцией силы на ось называется скалярная величина , равная произведению ее модуля F на косинус угла между силой и положительным направлением оси:

Проекцией силы на плоскость называется вектор , заключенный между проекциями начала и конца силы на эту плоскость.

В отличие от проекции силы на ось, проекция силы на плоскость является векторной величиной и характеризуется не только числовым значением, но и направлением в плоскости Oxy.

По модулю ,

где - угол между векторами .

8.Алгебраический момент силы относительно точки. Свойства момента.

Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо этой силы относительно выбранной точки, взятое со знаком плюс или минус.

Плечом силы относительно выбранной точки называют длину перпендикуляра опущенного из этой точки на линии действия силы.

Момент силы считают положительным, если под действием силы тело стремиться повернуться относительно выбранной точки против хода часовой стрелки, если по ходу часовой стрелки, то момент будет отрицательным.

Обозначают алгебраический момент силы 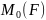. Сила не дает момента, если линия действия проходит через точку, относительно которой определяется момент: .

9. Векторный момент силы относительно точки. Свойства момента силы.

Векторным моментом силы относительно точки называют вектор, приложенный в этой точке и равный по модулю произведению силы на ее плечо относительно точки. Векторный момент силы перпендикулярен плоскости, проведенной через вектор силы и точку, и направлен таким образом, чтобы с его конца можно было бы видеть «стремление» силы вращать тело против хода часовой стрелки.

Векторный момент обозначают

Векторный момент можно определить из векторного произведения вектора на вектор :

По правилу векторного произведения вектор направлен перпендикулярно плоскости, образованной

и , в ту сторону, откуда кратчайший поворот вектора к вектору виден против хода часовой стрелки, т.е. векторное произведение совпадает с векторным моментом .

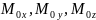- где - проекции векторного момента на соответствующие оси координат.

Модуль векторного момента:

.

10.Момент силы относительно оси. Свойство момента силы.

Моментом силы относительно оси называют произведение проекции силы на плоскость, перпендикулярную оси с плоскостью, взятую со знаком плюс или минус.

Момент силы относительно оси будет положительным, если проекция силы на плоскость, перпендикулярную оси, стремиться повернуться против хода часовой стрелки вокруг положительного направления оси.

, где - плечо силы относительно точки О пересечения оси и плоскости 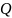; - проекция силы F на плоскость .

Момент силы относительно оси равен нулю если:

1. Сила параллельна оси

2. Линия действия силы пересекает ось.

11.Зависимость между моментом силы относительно точки и оси, проходящей через эту точку.

Определим момент силы относительно точки О пересечения плоскости и оси по формуле

Учитывая, что координата точки приложения силы по оси 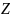равна нулю, т.е. :

Момент сил относительно оси равен проекции векторного момента силы на ось , а также моменту силы относительно точки О:

.

Момент силы относительно оси равен проекции векторного момента этой силы относительно точки на ось, проходящую через эту точку.

12.Аналитические выражения моментов силы относительно осей координат.

Аналитические выражения моментов силы относительно осей координат:

13.Пара сил. Алгебраический момент пары сил. Свойства момента пары сил.

Парой сил называют неупрощаемую систему двух равных по модулю и противоположно направленных параллельных сил с несовпадающими линиями действия.

Пару сил нельзя заменить одной силой, т.е. она не имеет равнодействующей. Пара сил характеризуется плоскостью действия, величиной момента пары и направлением вращения. Пара сил определяется векторным моментом пары. Он является вектором, перпендикулярным плоскости действия пары, и направлен в сторону, откуда видно вращение пары против хода часовой стрелки. По модулю векторный момент равен произведению одной из сил пары на плечо пары. Пару сил обозначают

,

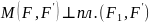Модуль момента:

Свойства пары сил.

Не меняя направление вращения пары сил и модуль ее момента: 1) Пару сил можно перемещать в плоскости ее действия и поворачивать. 2) Пару сил можно переносить в другую плоскость, параллельную плоскости действия пары. 3) У пары сил можно одновременно менять модуль силы и плечо пары.

14. Векторный момент пары является свободным вектором и может быть приложен к любой точке твердого тела. Это объясняется тем, что сумма векторных моментов сил, входящих в пару, всегда равна векторному моменту пары.

Две пары сил, действующие на одно и то же твердое тело и лежащие в пересекающихся плоскостях, эквивалентны одной паре сил, векторный момент которой равен сумме векторных моментов исходной пары сил.

30. Вычисление главного момента и главного вектора произвольной плоской системы сил. Частный случаи приведения плоской системы сил к центру.

Модуль главного вектора:

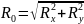
Где

( - проекции главного вектора на соответствующие оси координат).

Модуль главного момента относительно выбранного центра приведения 0:

Где

16. Теорема об эквивалентности двух пар сил, расположенных в одной плоскости .И о перемещении пары сил в плоскость параллельную плоскости её действия

Теорема 1: (об эквивалентности) пару сил действуэщую на твёрдое тело можно заменить другой парой сил расположенной в той же пл-ти действия и имеэщую с первой парой одинаковый алгебраический моментСледствие:1) пару сил можно как угодно поворачивать и переносить в пл-ти её действия.2) у пары сил можно ищменять плечо и силы, сохраняя алгебраический момент и пл-ть действия

Теорема 2. Действие пары на абсолютно твердое тело не из­менится, если ее перенести в любую плоскость, параллельную плоско­сти действия данной пары.

Пусть мы имеем пару сил (F1 F2) с плечом АВ (рис. 1.26, б). Перенесем плечо АВ в плоскость, параллельную плоскости действия данной пары, и присоединим к точкам А1В1 две системы сил, эквива­лентные нулю. Тогда (F1 F2) ~ (F1 F2, F3, F4, F5, F6). Далее, складывая силы F2 и F4, а также F1 и F5 и отбрасывая получившиеся взаимно урав­новешенные равнодействующие, получим:

(F1, F2) ~ (F1 F2, F3, FA, F5, F6) ~(R1 R2, F3, F6) ~ (F3, F6).

Отсюда следует, что плоскость пары действительно можно пе­реносить параллельно ей самой, не изменяя при этом оказываемого на тело действия.2 пары сил называют эквивалентными,если они обладают геометрически равными моментами т.е. эти пары имеют одинаков. По модулю моменты.

15, Вектор-момент пары и его направление. Теорема о сумме моментов сил пары

Численное значение момента пары равно произведению величи­ны одной из сил г.ары на плечо этой парыУсловились считать положительным момент такой пары, кото­рая стремится повернуть тело против вращения часовой стрелки, и от­рицательным - момент пары, которая стремится повернуть тело по на­правлению вращения часовой стрелки (рис. 1.23). Тогда алгебраическая величина момента пары (F1 F2) может быть записана так:

Очевидно, что момент пары равен моменту одной из ее сил от­носительно точки приложения другой.Кроме направления вращения и числового значения момента действие пары на тело, а следовательно, и ее момент зависят от того, как расположена плоскость действия пары, поэтому момент пары обладает определенным направлением в пространстве и, следовательно, есть ве­личина векторная.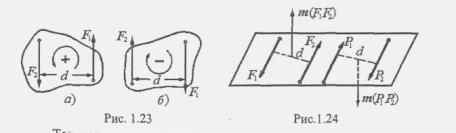 Так как направление плоскости в пространстве определяется направлением прямой, перпендикулярной к этой плоскости, то вектор, изображающий момент пары, направляют перпендикулярно плоскости действия пары. Длина этого вектора берется равной величине момента пары. Сторона, в которую направлен вектор-момент пары, должна характеризовать направление вращения пары (рис. 1.24).

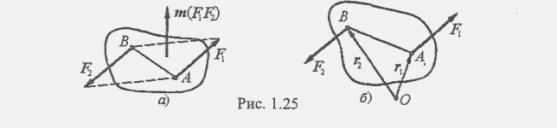Итак, момент пары есть вектор, перпендикулярный к плоско­сти действия пары, направленный в ту сторону, откуда поворот тела данной парой виден происходящим против хода часовой стрелки.Легко видеть, что момент пары численно равен площади парал­лелограмма, построенного на силах пары (рис. 1.25, а). Следовательно, вектор-момент пары равен векторному произведению векторов AB и F, Чтобы лучше пояснить понятие момента пары сил, докажем следующую теорему.Сумма моментов сил пары относительно любого центра равна моменту пары.В самом деле, возьмем произвольный центр О и проведем из него радиус-векторы гх и г2 в точки А и. В, где приложены силы пары (F1 F2) (рис. 1.25, б). Тогда

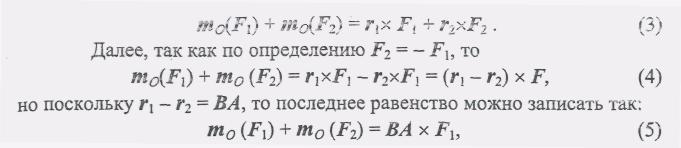
что и требовалось доказать.Понятие момента пары можно было бы определить как сумму моментов сил пары относительно некоторой точки. Из доказанной тео­ремы следует, что эта сумма не зависит от выбора точки и совпадает с введенным выше определением момента пары.