Вопрос 51. Проверка нормальности закона распределения вероятности результата измерения по виду гистограммы.

При обработке экспериментальных данных существенное значение

имеет вопрос о том, подчиняется или нет результат измерения нормальному закону распределения вероятности. Непротиворечивость такой гипотезы должна быть обязательно проверена.

Поскольку ошибки искажают эмпирический закон распределения вероятности результата измерения, постольку проверка предположения об его нормальности производится после исключения ошибок.

П равдоподобна или нет гипотеза о том, что результат измерения подчиняется нормальному закону распределения вероятности, можно определить уже по виду гистограммы, построенной на основании экспериментальных данных. Наглядность отображения гистограммой закона распределения вероятности результата измерения зависит от соблюдения следующих правил при ее построении:

1) интервалы , на которые разбивается ось абсцисс, следует выбирать, по возможности, одинаковыми;

2) число интервалов k устанавливать в соответствии со следующими рекомендациями:

Число измерений	Рекомендуемое число интервалов
40-100 100-500 500-1000 1000-10000	7-9 8-12 10-16 12-22

3) масштаб гистограммы выбирать так, чтобы ее высота относилась к основанию, примерно, как 5 к 8.

И ногда по виду гистограммы можно с большой уверенностью заклю­чить, что результат измерения подчиняется (или не подчиняется) нормаль­ному закону распределения вероятности. Если, например, гистограмма имеет вид, показанный на рис. 1, а, то результат измерения определенно не подчиняется нормальному закону. Если же гистограмма имеет вид, показанный на рис. 1, б, то возникает сомнение: достаточно ли хорошо она соответствует теоретической кривой нормального закона распределе­ния плотности вероятности, показанной пунктиром? Для разрешения это­го сомнения нужно иметь правило, руководствуясь которым можно было бы принимать то или иное решение.

Вопрос 52. Проверка нормальности закона распределения вероятности результата измерения по критерию к. Пирсона.

Существует несколько так называемых критериев согласия, по которым проверяются гипотезы о соответствии экспериментальных данных тому или иному закону распределения вероятности результата измерения. Наиболее распространенным из них является критерий К. Пирсона. При использовании этого критерия за меру расхождения экспериментальных данных с теоретическим законом распределения вероятности результата измерения принимается сумма квадратов отклонения частостей m_i /n от тео­ретической вероятности Р_i попадания отдельного значения результата из­мерения в i-й интервал, причем каждое слагаемое берется с коэффициен­том n / P_i:

Если расхождение случайно, то подчиняется -распределению (хи-квадрат распределению К. Пирсона).

Вопрос 53. Проверка нормальности закона распределения вероятности результата измерения по составному критерию.

_{При проверке нормальности закона распределения вероятности резуль}­тата измерения применение критерия К. Пирсона дает хорошие результа­ты только, если n > 40 ... 50. При 10 . . . 15 < n < 40 ... 50 применяется так называемый составной критерий. Сначала рассчитывается и проверяется выполнение условия

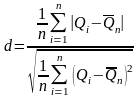
где d_min и d_max зависят от вероятности Р*, с которой принимается решение, и находятся по таблице.