37. Расчёт косозубых цилиндрических передач на изгиб
Наклонное
расположение зубьев увеличивает их
прочность на изгиб и уменьшает динамические
нагрузки. Это учитывается введением в
расчётную формулу прямозубых передач
поправочных коэффициентов 
и
.
Формула проверочного расчёта косозубых
передач
(2.3.41),
где
YF - коэффициент формы зуба выбирают по
эквивалентному числу зубьев zv; 
-
коэффициент, учитывающий наклон зуба;
-
коэффициент распределения нагрузки по
ширине венца определяют по аналогии с
прямозубыми передачами;
=
0,81-0,91 - коэффициент распределения
нагрузки между зубьями;
-
коэффициент нагрузки, учитывающий
дополнительные динамические нагрузки
=1,2
при твердости зубьев не больше 350НВ,
=
1,1 при твердости зубьев более 350 НВ.
Нормальный модуль зубьев mn определяют
по аналогии с прямозубыми передачами.
При некоторых средних значениях
коэффициентов получим формулу для
приближенного определения модуля
косозубых передач
(2.3.42),
и
для шевронных передач
(2.3.43),
При
проверке по формуле (2.3.41):
можно
получить
значительно
меньше
,
что не является недопустимым, так как
нагрузочная способность большинства
передач ограничивается контактной
прочностью, а не прочностью на изгиб.Если
расчётное значение
превышает
допускаемое, то применяют колёса,
нарезанные с положительным смещением
инструмента, или увеличивают
m;
>
означает,
что в передаче из данных материалов
решающее значение имеет не контактная
прочность, а прочность зубьев на изгиб.
На практике к таким передачам относятся
передачи с высокой твёрдостью рабочих
поверхностей зубьев – 51…63HRCэ (цементация,
нитроцементация, азотирование).
Проектировочный расчёт таких передач
следует выполнять с целью обеспечения
прочности зубьев на изгиб по форме
определения минимально допустимого
модуля m, а затем выполнить проверочный
расчёт зубьев на контактную прочность.
38. Передачи коническими колесами. Классификация. Кинематика и геометрия конических передач.
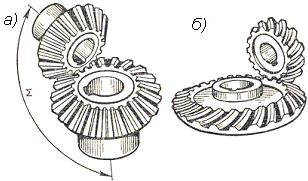Рисунок
2.3.17 Коническая прямозубая передача а),
передача с круговым зубом б)
Применяют
во всех отраслях машиностроения, где
по условиям компоновки машины необходимо
передать движение между пересекающимися
осями валов. Конические передачи сложнее
цилиндрических, требуют периодической
регулировки. Для нарезания зубчатых
конических колес необходим специальный
инструмент. В сравнении с цилиндрическими
конические передачи имеют большую массу
и габарит, сложнее в монтаже. Кроме того,
одно из конических колёс, как правило
шестерня, располагается консольно. При
этом, вследствие повышенной деформации
консольного вала, увеличиваются
неравномерность распределения нагрузки
по ширине зубчатого венца и шум.
Конические
колёса бывают с прямыми и круговыми
зубьями.
Передаточное числа
при межосевом угле 
(2.3.44)
Для конической прямозубой передачи рекомендуется u=2, 2,5; 3,15; 4, для передачи с круговыми зубьями возможны более высокие значения u; наибольшее значение u=6,3.
Геометрические параметры конического зубчатого колеса
Основные геометрические размеры определяют в зависимости от модуля и числа зубьев. Высота и толщина зубьев конических колёс постепенно уменьшается по мере приближения к вершине конуса. Соответственно изменяются шаг, модуль и делительные диаметры, которых может быть бесчисленное множество. Основные геометрические размеры имеют обозначения, принятые для прямозубых конических передач рис. 2.3.18.
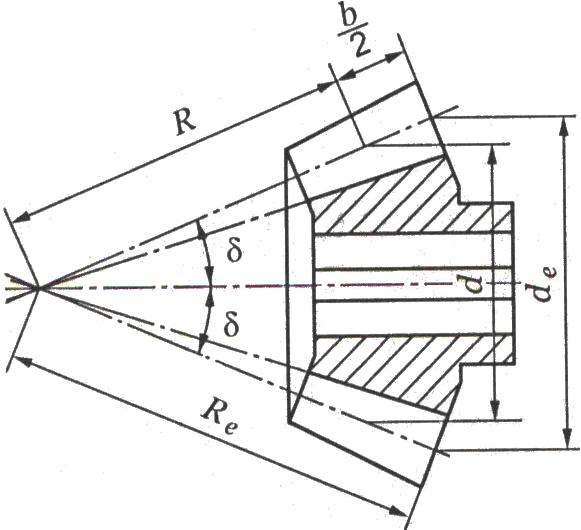Рисунок
2.3.18 Геометрия конического колеса
Внешний
диаметр 
:
(2.3.45)
где 
-
максимальный модуль зубьев – внешний
окружной модуль, полученный по внешнему
торцу колеса. Внешнее конусное расстояние
(2.3.46)
Среднее
конусное расстояние 
(2.3.47),
где b – ширина зубчатого венца
колеса
(2.3.48)
-
коэффициент ширины зубчатого венца
относительно внешнего конусного
расстояния.
-
углы делительных конусов;
Средний
модуль
(2.3.49)
Средние делительные диаметры:
(2.3.50)
(38.2)
(2.3.51)
В
соответствии с исходным контуром
прямозубых конических колёс радиальный
зазор c=0,2
,
тогда
внешняя высота головки
зуба 
(2.3.52)
и
внешняя высота ножки зуба 
(2.3.53).
Внешние
диаметры вершин зубьев
(2.3.54)
(2.3.55)
Угол
ножки зуба 
(2.3.56).
Угол
головки зуба 
; 
(2.3.57)