3.3 Элементы конструкции пк

Конструктивно ПК выполнены в виде центрального системного блока, к которому через разъемы подключаются внешние устройства: дополнительные устройства памяти, клавиатура, дисплей, принтер и др.

Системный блок обычно включает в себя системную плату, блок питания, накопители на дисках, разъемы для дополнительных устройств и платы расширения с контроллерами-адаптерами внешних устройств.

На системной плате (часто ее называют материнской платой), как правило, размещаются:

• Микропроцессор;

• Математический сопроцессор;

• Генератор тактовых импульсов;

• Блоки (микросхемы) ОЗУ и ПЗУ;

• Адаптеры клавиатуры, НЖМД и НГМД;

• Контроллер прерываний;

• Таймер и др.

4. Представление информации

Компьютерная информация делится на 3 группы:

1. Системная информация.

2. Программная информация.

3. Обрабатываемая информация.

Системная информация создается вместе с программным обеспечением компьютера.

Программная информация формируется самим программистом в зависимости от конкретной задачи.

Обрабатываемая информация в свою очередь делится на 3 вида:

1. Числовые данные.

2. Логические данные.

3. Текстовые данные.

Все виды обрабатываемой информации кодируются с помощью чисел. Числа записываются с помощью системы счисления. Система счисления – совокупность правил, с помощью которых записывается конкретное число, при этом основанием системы называется число знаков данной системы, позволяющих записывать все множество чисел.

В зависимости от способа изображения чисел системы счисления делятся на позиционные и непозиционные.

В позиционной системе счисления количественное значение каждой цифры зависит от ее места (позиции) в числе.

5 55

50

5

500

В непозиционной системе счисления количественное значение цифры не зависит от ее положения в числе и определяется только ее графическим обозначением. Примером такой системы является римская система счисления (IX, XIV).

В вычислительной технике находят применение двоичная, восьмеричная, десятичная, шестнадцатеричная системы счисления.

При любом основании системы счисления каждое конкретное число может быть представлено полиномом:

a _n a_n-1…a₀,b₁ b_2…b_m= a_nRⁿ +a_n-1R^n-1 +…+ a₀R⁰ +b1R^-1 +b₂R^-2 +…+b_mR^-m

целая часть дробная часть

где нижние индексы определяют местоположение цифры в числе (разряд).

R – основание системы счисления;

a_i - цифра целой части числа.

b_i - цифра дробной части числа.

Наибольшее распространение в ЭВМ имеет двоичная система счисления. В этой системе используются только две цифры 0 и 1.

Для перевода десятичного числа в восьмеричную, шеснадцатиричную или двоичную систему счисления в общем случае проводят два расчетных этапа.

Целую часть числа делят на основание новой системы счисления до тех пор, пока частное от деления не станет меньше основания. В новой системе счисления целая часть записывается в виде остатков от деления начиная с последнего частного справа на лево. Дробная часть в новой системе счисления получается умножением дробной части числа в старой системе на основание новой системы, до тех пор пока дробная часть не станет = 0 или не будет достигнута требуемая точность. Дробь в новой системе счисления запишется в виде целых частей от полученных произведений, начиная с первого. Перевод чисел, имеющих и целую и дробную часть, осуществляется в два этапа: сначала переводится целая часть числа, а затем дробная. Обратный перевод из двоичной, восьмеричной или шеснадцатиричной системы счисления в десятичную осуществляется с помощью записанного полинома:

Пример: 25,375₁₀

1

2

) 10 2:

2 5 2 0 375

2 4 12 2 0 750

1 12 6 2 1 500

0 6 3 2 1 000

0 2 1

1

25,375₁₀=11001,011₂

2

8

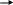) 10 8

а ) 25 8 б) 0 375

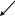24 3 3 000

1

25,375₁₀ = 31,3₈

3

16

) 10 16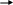

a ) 25 16 б) 0 375

16 1 6 000

9. 

25,375₁₀ = 19,6₁₆

Осуществим обратный перевод из двоичной, восьмеричной и шестнадцатеричной в десятичную.

4) 2 10:

11001,011₂=12⁴+12³+02²+02¹+12⁰+02^-1+12^-2+12^-3=16+8+1+0,25+0,125=25,375

11001,011₂=25,375₁₀

5) 8 10:

31,3₈ = 38¹+18⁰+38^-1=24+1+0,375=25,375

31,3₈ = 25,375₁₀

6) 16 10:

19,6₁₆=116¹+916⁰+610^-1=16+9+0,375=25,375

Восьмеричная и шестнадцатеричная системы счисления используются при работе с языком программирования низкого уровня, т.е. наиболее приближенным к языку компьютера (так называемое программирование в кодах машины). При программировании в кодах машины наиболее удобной записью является восьмеричная и шестнадцатеричная система. В отличие от двоичной системы счисления числа получаются более краткими.

Для перевода чисел из двоичной системы в восьмеричную и шестнадцатеричную и наоборот, удобно осуществлять с помощью следующей таблицы записи чисел.

Двоичное число	Восьмеричное число	Десятичное число	Шестнадцатеричное число
0000	0	0	0
0001	1	1	1
0010	2	2	2
0011	3	3	3
0100	4	4	4
0101	5	5	5
0110	6	6	6
0111	7	7	7
1000	10	8	8
1001	11	9	9
1010	12	10	A
1011	13	11	B
1100	14	12	C
1101	15	13	D
1110	16	14	E
1111	17	15	F
10000	20	16	10
10001	21	17	11

Перевод чисел из двоичной системы в восьмеричную и обратно.

Основание восьмеричной системы представляет собой целую степень числа 2 (8 = 2³), поэтому для перевода восьмеричного числа в двоичное, каждая его цифра представляется тремя двоичными или триадой.

3 1 , 3₈ =11001,011₂

011 001 011

Для обратного перевода двоичное число разделяют на триады вправо и влево от запятой. Если в крайних триадах оказывается количество цифр меньше трех, то они дополняются нулями.

011 001,011₂ = 31,3₈

Перевод чисел из двоичной системы в шестнадцатеричную и обратно.

Основание шестнадцатеричной системы представляет собой целую степень числа 2 (16 = 2⁴). Поэтому перевод здесь аналогичен предыдущему, только для представления одной цифры используются тетрады (4 цифры).

1 9 , 6₁₆=11001,011₂

0001 1001 0110

0001 1001,0110₂ = 19,6₁₆

Иногда компьютеры работают в десятичной системе счисления. При этом используется так называемая двоично-десятичная система. Каждая десятичная цифра в двоично-десятичной системе кодируется с помощью тетрад.

25,375₁₀=0010 0101,0011 0111 0101_2-10

Арифметические действия с двоичными числами.

1. Сложение.

0+0=0

0+1=1

1+0=1

1+1=10

2. Вычитание.

0-0=0

1-0=1

1-1=0

10-1=1

3. Умножение.

00=0

01=0

10=0

11=1

Пример: сложение двух двоичных чисел.

1 011

1011

10110

вычитание двух двоичных чисел.

1010

0 110

0 100

умножение двух двоичных чисел.

1 010

101

1010

1010

110010