Глава II.

ДАВЛЕНИЕ И УСИЛИЕ НА ВАЛКИ, МОМЕНТЫ И МОЩНОСТЬ ПРОКАТКИ

1. Давление при равномерной деформации металла

Для того чтобы облегчить понимание значения и влияния различных факторов в реальном процессе прокатки, введем понятие идеального процесса прокатки и рассмотрим его основные зависимости.

Идеальным процессом прокатки называется такой про­цесс пластической деформации металла вращающимися валками, при котором в любом вертикальном сечении зоны деформации горизонталь­ные скорости пластического течения металла постоянны по высоте этого

сечения и все волокла этого сечения получают (удлинение).

Идеальный процесс прокатки является равномерным и симметрич­ным относительно оси х (скорости и диаметры верхнего и нижнего вал­ков одинаковы). Все приведенные в гл. I формулы справедливы именно для этого равномерного (идеального) процесса про катки.

Геометрической зоной деформации в каждый данный момент време­ни является объем металла, ограниченный дугами захвата АВ — а и вер­тикальными плоскостями входа металла в валки и выхода из валков, проходящими соответственно через точки А и В (см. рис. 1.30).

Процесс прокатки — обжатия металла вращающимися валками — возможен только благодаря контактным силам трения; иначе говоря, работа прокатки (деформации металла) осуществляется только кон­тактными силами трения, возникающего по дугам АВ при вращении валков.

Контактные силы трения создают объемное напряженно-деформиро­ванное состояние металла в зоне деформации. Таким образом, постоян­ство скоростей и вытяжек всех волокон в любом вертикальном сечении обусловливает также постоянство горизонтальных напряжений в этом сечении, т.е. о_Ху = const.

Идеальный процесс прокатки возможен только для весьма широ­кой полосы, когда деформация в направлении ширины настолько незна­чительна, что ею можно пренебречь. Отсюда следует, что идеальный процесс прокатки соответствует такому объемному напряженному со­стоянию металла в зоне деформации, при котором деформация осущест­вляется только в двух направлениях — по осям х и у, а деформация в третьем направлении — по оси г равна нулю. Поэтому при анализе на­пряжении в объеме деформируемого металла можно применять уравне­ния пластичности па основе энергетической теории Губера — Мизеса — Генки для плоской деформации ^=0) в общем виде (fie в главных напряжениях, см. с. 20)

К — **)* -f 4т%, - (2т_шах)'² /г², (II. 1)

где ттах — максимальное касательное напряжение при пластической де­формации (константа пластичности), равное а_д/ КЗ ^0,58а_д; к — кон­станта уравнения пластичности, равная 2т_тах ~ 1»15 <т_д (см. с. 19).

При отсутствии разности скоростей пластического течения металла по высоте любого сечения в зоне деформации (отсутствии внутренних сдвигов) касательные напряжения х_ху=г_ух (рис. 11.1) в этих сечениях равны нулю (за исключением точек на контактной поверхности, где име­ются контактные силы трения т.,Поэтому для идеального процесса cry = а 1 н <у_х=Оз и для любого вертикального сечения справедливо урав­нение пластичности (II.I) в главных напряжениях

o_L — оз = k. (II.2)

Рассматривая бесконечно малый элемент толщиной clx в зоне дефор­мации и полагая ввиду небольшой величины текущего угла a* cos а*« ^ 1 и радиальное (нормальное) давление р_х равным вертикальному напряжению (т.е. рл/cosa_x&р_хто\), уравнение пластичности для иде­ального случая процесса представим в следующем виде:

Рх — °х — k = const; (II.3)

dp_x = do_x.

Для последующего определения полного давления металла на валки Р (или валков на металл) необходимо знать радиальное давление р_х пе­ременное по дуге захвата а (по се проекции на горизонталь, называе мой длиной контакта /). Однако в уравнении (11.3) два неизвестных: р_х и о*, поэтому для их нахождения необходимо иметь второе уравнение с этими неизвестными.

С этой целью запишем условие равновесия всех внешних и внутрен­них сил, действующих па бесконечно малый элемент шириной dx с вы*

сотой h_x = 2y в зоне деформации в сечении па расстоянии х от оси вал­ков (см. рис. II.1); при этом учтем, что контактные (касательные) напряжения т_Л- направлены в противоположные стороны относительно нейтрального сечения, а напряжения р_х являются радиальными (нор-

Рнс. 11.1. Эпюры распределения нормальных (радиальных) давлений и касательных напря­жений (контактных сил трения) по дуге захвата (по ее проекции на горизонталь)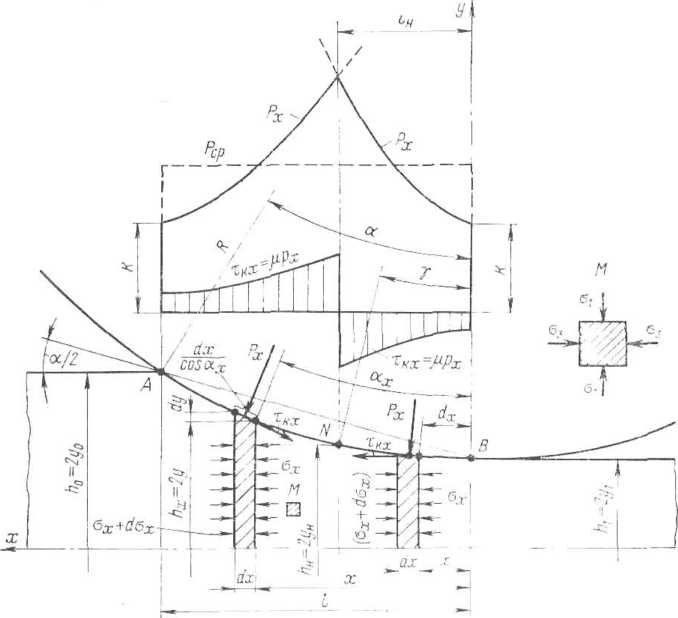

мольными). Оба напряжения р_х и о.* действуют на площадку шириной

dxlcos а_х:

2Х = р_х -^ch ■ sin a,. I t_v——— cos a_v -j- cr_Y„ — ( a,, -j- do_x) (y -\- cly) - 0. cos <x_x " ‘ cos a_x ' '^v

Заменяя tga_X=dy/dx и разделив все члены на ydx, получим

do_x Рх — о_х dy , т_х _q

dx у dx у

или, используя уравнение пластичности (II.3):

.^dpJL L A-L l. ^Тх — о. (П.4)

dx у dx у

Здесь и далее верхний знак перед т_х соответствует зоне отставания, а нижний — зоне опережения (т. е. слева и справа от нейтрального сече­ния, характеризуемого точкой А' на дуге захвата).

Это уравнение является основным для определения величины р* и оно называется д и ф ф ерей ц и а л ьп ы м у р ав не и и е м д а в л е - н и й при идеальном п р о ц е с с е п р о к а т к п.

Для решения этого уравнения необходимо знать закон изменения контактных напряжений (сил трения) %_х по дуге захвата.

Постоянство скоростей пластического течения всех волокон металла в любом вертикальном сечении при идеальном процессе прокатки дол­жно вызывать скольжения по контактной поверхности, т. с. наличие раз­ности горизонтальных скоростей металла с_м.ч и валков и_вх по всей дуге

АВ, за исключением точки N нейтрального сечения, где эти скорости равны и скольжение отсутствует. Соответственно этой разности скоро­стей по контактной поверхности действуют контактные силы трения х_х. Поскольку при прокатке металл деформируется пластически, физичес­кая природа этих контактных сил трения будет отличаться от сил тре­ния, возникающих по закону Кулона при обычном скольжении трущих­ся поверхностей в условиях весьма малой упругой деформации. Однако законы контактного трения при больших пластических деформациях ис­следованы еще недостаточно и не имеют точного математического вы­ражения.

Поэтому для идеального процесса прокатки считаем действительным закон Кулона о трении скольжения: т_х — (гр_х, т.е. сила трения (каса­тельное напряжение) пропорциональна нормальному давлению при по­стоянном значении коэффициенте) контактного трения.

В этом случае дифференциальное уравнение нормальных давлений при идеальном процессе прокатки имеет вид

^dpx _± jx-P*- = 0. (II.4а)

dx у dx ' dx

Это уравнение разрешимо относительно р_х, однако при подстановке текущих координат у и х любой точки на дуге АВ (соответствующей уравнению окружности, центр которой смещен по отношению к началу координат на величину f/i—fti/2) получается весьма сложная конечная формула, неудобная для практического пользования.

Для получения более простых и достаточно точных расчетных фор­мул предложено несколько способов; рассмотрим два из них, которые дают наиболее приемлемые результаты.

Первый способ. Заменяем процесс прокатки (осадки) металла ци­линдрическими валками процессом осадки металла между параллель­ными плитами (штампами), причем в зоне отставания расстояние меж­ду плитами равно hx — 2yo—ho~Q.ons{, а в зоне опережения h_x~2y₁ — =h_{ —const (ступенчатые штампы). В этом случае dy = 0, dy/dx~0, дифференциальное уравнение (11.4а) примет простой вид и решение его приводит к простым и удобным для анализа формулам:

а) для зоны отставания (дуга AN)

dpjdx -f рр_х (2/h₀) = 0; J dpjp_x = — 2p/h₀ f dx;

In p_x = — (2\xlho) x 4- C₀.

При x — l (сечение входа металла в валки) а_Л=0, поэтому, согласно уравнению пластичности (II.3):

Р_х ~ Рл = ^Со = ^{1п к} + ²И (^l/ho).* ^]п (Pj^k) = ^tno (¹ — ^х//);

m_y) 2ц (//Л₀);

pjk ; (115) j

б) для зоны опережения (дуга BN)

dpjdx — рр_х (2Ih_x) = 0; j dpjp_x = 2\Uh_x [ dx- In p_x -- (2\Uh_x) x + C_x.

При ;c=0 (сечение выхода металла из валков) (т*=0, поэтому, cor- I ласно уравнению пластичности (II.3):

р_я = р_в = Ci = In k; In (pjk) m₁(xll);

m_x = 2[i(lfh₁)\ pjk — (П.6)

Согласно полученным уравнениям (II.5) и (11.6), от сечения входа I металла в валки и сечения выхода металла из них но направлению к г нейтральному сечению давления возрастают по экспоненциальным кри­вым. Точка пересечения кривых при х—1_п определяет положение нейт­рального сечения

т₀(\ —/„//) = т._х (IJI),

откуда

t_H = ^= 1/2(1 — е)/(I —е/2) < 1/2, (II.7)

где е=(Ло—hi)/h₀ — относительное обжатие металла.

Таким образом, нейтральное сечение расположено правее середины дуги захвата (/_н<//2).

Среднее по длине контакта давление соответствует средней ордина­те эпюры Рх, т. е.

I I

Pep

Гр_хdx + _Рхdxl = у|[ e^m'*"dx + j‘e^m'^{l~^xmdx

p_cplk = Mm{e^,n— 1), где m — u ——

—=к

h _Cp ^ ^ 2(1 — e)

Согласно уравнению (П.8), среднее давление зависит от одного па­раметра га. С увеличением т среднее давление резко возрастает (кри­вая А, см, рис. II.2).

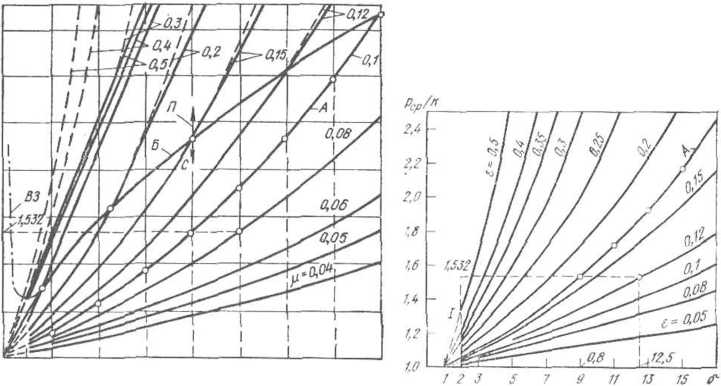
Рис. 11.2. Кривые зависимости среднего давления (от­ношения р_ср/к) от параметра Uh _Ср при различных значениях коэффициента контактного трения:

А — кривая, зависящая от одного параметра т: 5 — граница скольжения; В. 3 — кривая влияния внешних зон; П — область наличия прилипания по дуге захвата; С — область скольжения

Рис. II.3. Кривые зависимости отношения Р_ср Ik от параметра б при различных зна­чениях относительного обжатия е:

А — кривая, зависящая от одного парамет­ра т; /—граница естественного захвата металла валками

I J ! ( i I I ' I

О йи 0,4 0,6 0,8 1,0 1,2 1,йт(А)

Рср к

2,4

Представим отношение l/h_cр в следующем виде:

l!h_cv = llh_Q [2/(2 - е)] llhy [2(1— в)/(2 - е)].

Очевидно, что отношение (параметр) l/h_cр одновременно учитывает влияния толщины деформируемого металла (к₀ пли h_:) и степень обжа­тия е, т. е. является наиболее универсальным (по сравнению с l/h_Q или l/fh).

На рис. II.2 представлены кривые зависимости среднего давления (отношение р_сР/к) от отношения l/hc._Р при различных значениях коэф­фициента трения = const. Очевидно, что с увеличением ///г_ср давление резко возрастает, особенно при больших значениях р..

Второй способ (А. И. Целикова). Дугу эахвата АВ = а заменим хор­дой АВ, наклоненной к горизонтали над углом a/2 = const (см. рис.

2. 1)); тогда ij = h\f2-j-(ct/2)x; dy/dx=a/2 = const.

В результате решения уравнения (II.4а) получим формулу А. И. Цс- ликова для среднего давления по длине контакта:

pjk = 12 (J - е)]./1е (6 - 1 ))(hM(hM^b - П; (П.9)

положение нейтрального сечения

|/б

6+

л I

(II.9а)

hn/hi

(11.10)

где б = 2рХ'Д/г = 2\х!а(при ДА а/).

При больших значениях (практически при t)I>5) отношение асимптотически приближается к своему максимуму, равному

е/2).

(fciA)n, ах = I hJK = / 1/(1 — ё) ~ 1/(1

Формула (II.9) является более точной для случая прокатки по срав­нению с формулой (II.8) (для осадки ступенчатыми плитами). Однако она недостаточно наглядна, так как для определения p_cv надо сначала найти отношение h,_l/h_[ по формуле (П.9а). Для получения более про­стои и точной формулы для р_Ср примем среднегеометрическое [а не сред­неарифметическое, как в формуле (П.8)] значение высоты нейтрально­го сечения [см. уравнение (11.10)].

В результате получим (формула А. А. Королева)

Рс])

к

(Н.И)

fcr'c-Hl-

ЦК

В формулах (II.9) и (II.11) коэффициент 6 можно выразить через

= м

АЛ

Л|.|

= 2 ц

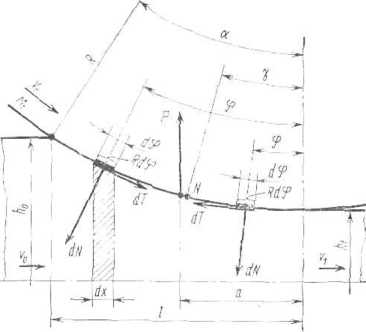
Ряс. 11.4. Элементарные силы d,N и dT. действу­ющие от валков на металл в зоне отставания (левее точки N) и и зоне опережения (правее точки N) при установившемся процессе прокатки

построенные по этим формулам кривые зависимости p_cv/k=f (6) (рис.

11. 3) аналогичны кривым, полученным по формуле (II.8). Так как фор­мулы (II.9) и (11.11) в явном виде учитывают относительное обжатие е, то их следует считать более приемлемыми для прокатки, чем формула , для осадки (11.8). Разница в

подсчетах среднего давления по этим формулам для £<0,4 не пре­вышает 4—8 %.

Полное усилие на валок соот­ветствует площади эпюры давле­нии по длине контакта (для ши­рины полосы b = 1), т. е.

Р = Рс р/, (11.11а)

где I — длина контакта металла с валком (1~ )' ЯА1г).

Определим теперь момент, не­обходимый для вращения валков при прокатке.

Согласно рис. П.4, в зоне де­формации на бесконечно малый элемент шириной dx по элемен­тарной дуге Rdcf действуют от валков на металл нормальная си­ла dN=p_xRdq> и касательная си­ла трения dT=T_xRdq>. Действие этих сил от металла на валок будет об­ратным, поэтому очевидно, что нормальные силы d\^r, направленные по радиусу в центр валка, не создают момента (Л1м=0).

Момент прокатки определяется только контактными силами трения dT, направленными по касательной к окружности валка и противопо­ложные стороны в зонах опережения и отставания (правее и левее точ­ки JV, соответствующей нейтральному углу у).

Момент прокатки для одного валка (при ширине полосы b = 1) Мх — 1‘т_Л. R²dx[) — |'т_д. R²d(p.

у О

С некоторым допущением принимаем, что по всей дуге захвата а кон­тактные силы трения постоянны, т. е. т*=т_Ср (что равносильно также допущению, что p.v = Pcp, так как т_x = [ip_x)- Тогда получим (формула Баюкова)

М₁ - т_(:р (а - 2_Y) ^ т_ср /?² а (1 - 2у/а). (11.12)

Подставляя значение нейтрального угла по формуле (1.69) в урав­нение (11.12) и заменяя т_ср=цРср и Rat&l, получим

M_L = Ч,р_с I) /² = Ч_гР1 Ра = Ру[1, (И. 13)

где а — плечо приложения равнодействующей Р (усилия на валки); г[l — afl — коэффициент плеча приложения сила Р.

Таким образом, при принятом выше допущении T_x=T,-_p=const и p_x=p_cv=const плечо приложения равнодействующей давления метал­ла на валок равно половине длины контакта, т. е. ф=0,5.

В действительности, как указано выше, контактные силы трения т* и нормальные (радиальные) давления р_х не являются постоянными по дуге захвата (по длине контакта /, см. рис. II.1) и коэффициент ф не равен 0,5.

При идеальном процессе прокатки равнодействующая Р направлена вертикально через центр тяжести эпюры давлений р_х; значит, абсцисса центра тяжести эпюры х_с соответствует плечу а приложения равнодей­ствующей относительно центра валка. Момент прокатки (для одного валка) можно выразить как момент элементарных площадок (p_xdx) и приравнять его к моменту площади всей эпюры р_х: i

= )’ (р_х dx)x = Ра = р_сР la = р_ср 1 (1 pi) = р_ар ipi²,

6

поэтому точная формула для определения коэффициента плеча прило­жения равнодействующей имеет следующий вид:

	‘ 'н	1
“ф -- Рср	| (Pxdx)x	-|- ( (pxdx)dx
	0	"1a

Подставив значения р_х из уравнений (II.8) и (II.9), р_ср из формулы (II.11) и /„ из выражения (11.10), получим формулу для определения плеча приложения равнодействующей:

Для in■<0,5 можно принять с достаточной ТОЧНОСТЬЮ, ЧТО £?^m=l-j- ■ш+т²/2, тогда формула (П. 14) упрощается и принимает вид

* = ~ (^[ - ^е 44^ < 4“ • (И.:14а)

2. 1 — е/2

Очевидно, что при е^О величина г}- = 0₎5, т.е. равнодействующая приложена посередине дуги захвата. С увеличением в и т коэффициент плеча уменьшается незначительно. Так, для т— 2,0 получим: при ь-= 0,2 ф=0,47, а при r = 0,5 ij: = 0,43.

Анализ этих формул и соответствующие экспериментальные данные показывают, что плечо приложения равнодействующей по своей вели­чине равно (незначительно больше) абсциссе нейтрального сечения, т. е. Q —/и и ^,ф='фн^0,5

Момент прокатки для двух валков равен

М_пр = 2Ра = 2Р\\>1, (II.15)

где следует определять по формуле (11.14), (II.14а), а Р — по фор­мулам (II. 10), (П.11), (П.Па).