при прокатке готового профиля).

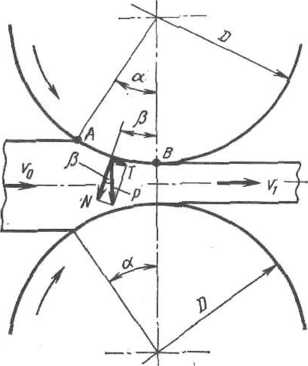
Ряс, 1.25. Силы, действующие от валков на металл при установившемся процессе прокатки

(Д h/R)

Прокатка

V,. Град

2) увеличить коэффициент трения, что возможно только в некото­рых случаях (при насечке валков, наварке на валках утолщений; это допустимо только при прокатке слитков и заготовок и недопустимо

В табл. 1.3 приведены значения максимальных углов захвата, установ­ленные практикой.

После выхода переднего конца по­лосы из валков наступит установив­шийся процесс прокатки: металл будет входить в валки с постоянной скоро­стью v₀ и выходить из них с постоян­ной скоростью v\. Если не учитывать незначительных по величине сил инер­ции, возникающих в зоне деформации при изменении горизонтальной скоро­сти металла от v₀ до Vi, т. е. считать, что металл движется равномерно, то равнодействующие Р сил N и Т долж­ны быть направлены вертикально (рис. 1.25) и приложены вблизи середины дуги захвата АВ, т. е.

р « а/2 = ц; а « 2ji. (1.55)

Таким образом, если каким-нибудь надежным способом обеспечива­ется захват металла, то угол захвата мог бы быть в 1,5—2 раза боль­ше, чем при условии свободного (естественного) захвата, и соответст­венно можно было бы увеличить обжатие металла за данный пропуск, т. е. в конечном счете, увеличить производительность стана. С этой целью иногда применяют принудительную задачу металла в валки (например, при помощи толкателя), при которой передняя грань полосы сминается о валки, и этим облегчает захват металла.

В некоторых случаях с целыо обеспечения захвата металла осуще­ствляют прокатку заготовок с предварительно скошенными на клин передними углами.

Уменьшение угла захвата при сохранении величины обжатия воз­можно при увеличении диаметра валков. Однако увеличение диаметра валков приводит к увеличению давления металла на валки (см. рис. 1.23), что во многих случаях нежелательно.

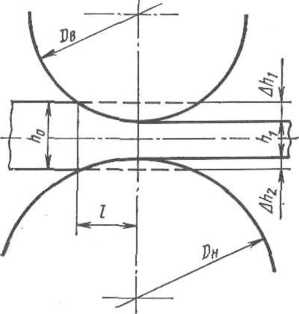
Длина зоны деформации

Рис. 1.27. К определению длины контакта I при прокатке металла в валках, имеющих неравные диаметры

Рис. 1.29. К определению длины контакта ме­талла с валками при упругом сплющивании валка

Как указано выше, геометрической зоной деформации называется область, ограниченная сверху и снизу дугами захвата и плоскостями входа металла в валки и выхода из валков (при b = 1, рис. 1.26).

Рис. 1.26. К определению длины контакта I (горизонтальной проекции дуги захвата)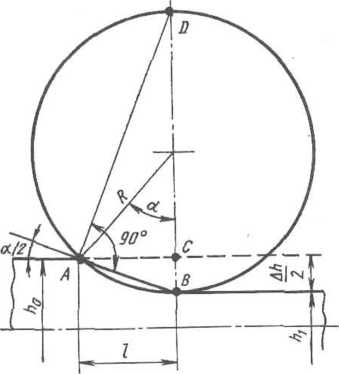

Рис. 1.28. Ширина контакта при сжатии упру­гого цилиндра, нагруженного силой Р, с не­сжимаемой (абсолютно жесткой) плоскостью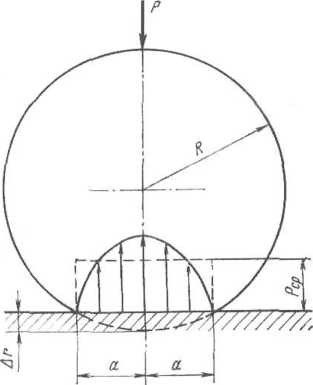

Горизонтальная проекция хорды дуги захвата АВ называется дли­ной зоны деформации (длиной контакта металла с валком) и обозна­чается через I.

Из рис. 1.26 следует, что

АВ/ВС =- BD/AB; АВ = VMh; (1.56)

АС = I = V АВ*— ВС² = VRAh — ДА^а/4. (1.57)

Так как второй член иод радикалом (Ah/2)² значительно меньше первого, то во многих случаях им можно пренебречь и считать, что длина зоны деформации равна'длине хорды, т. е. АС=АВ и

l^VRAh,

Its Razz Ah/a.

(1.58) (1.58a)

Для случая прокатки листов на станах, у которых диаметры валкоз различны (листовой трехвалковый стан, многовалковый несимметрич­ный стан), длина зоны деформации определяется по несколько изме­ненной формуле.

Согласно рис. 1.27 и формуле (1.58) получим h= V R\2Ah\\ /₂ = = V R₂2Ah₂, где Л/ii и Ah₂—обжатия со стороны первого и второго вал­ков, имеющих радиусы Ri и R₂, соответствующие £)_в и £>_н.

Принимая h^l₂^l и учитывал, что Ah=Ahi-\-Ah₂, получим

(1.59)

/ = КЯпрДЛ,

где R_np — приведенный радиус валков, RnD=2R\R₂/ (R\-\-R₂); при Ri = = R₂R_Dp = R'

При холодной прокатке тонких листов из стали и других твердых металлов и сплавов возникает значительное давление по длине контак­та металла с валками. Это давление вызывает упругое сжатие (сплю­щивание) валков и металла, которое искажает и увеличивает длину дуги захвата. В этом случае пользоваться формулой (1.58) для опреде­ления длины контакта нельзя, так как подсчеты по ней дают занижен­ные результаты (на 20—40 % и более).

Приращение длины контакта можно определить исходя из известной задачи Герца об упругом сжатии цилиндра, нагруженного силой Р и ле­жащего на несжимаемой плоскости (рис. 1.28). Под действием силы Р цилиндр упруго деформируется и ширина поверхности упругого контак­та по формуле Герца

2. (1.60)

   a = 4 VqkyR,

где q — давление на единицу длины цилиндра; k_y — коэффициент, зави­сящий от упругости материала цилиндра, равный 6_У=(1 — \ii)/nE\ р,„ и Е — соответственно коэффициент Пуассона и модуль упругости для ма­териала цилиндра.

Если заменить эллиптическую эпюру контактных давлений сжатия равновеликой прямоугольной эпюрой, то среднюю ординату (среднее) давление р_Ср) можно выразить через погонную нагрузку следующим об­разом P=qL = 2ap_cvL, откуда q — 2ap_cv, где L — длина цилиндра.

Подставляя это значение в уравнение (1.60), получим

(1.61)

a = 8kу Rp_CI>; p_cp = 1/4 V q!(k_y R).

Чтобы обжать металл одним валком на величину Д/г/2, необходимо валок из исходного положения (рис. 1.29, пунктир) сместить вниз на ве­личину BD—Ar, равную упругому сплющиванию валка (упругим сжа­тием полосы можно пренебречь, так как при небольшой толщине поло­сы ее упругая деформация весьма мала).

При этом контактная поверхность исказится и дуга контакта при уп­ругом сплющивании валка получит вид кривой А'ВВПриращение длины контакта произойдет как слева (АА'), так и справа (ВВ') от оси валков, причем второе значительно больше первого.

Определим длину сплющенной кривой контакта (ее проекцию на го­ризонтальную ось). Из рис. 1.29 очевидно, что

^xo = (А' ОУ — (DO' —CB — BDf « RAh + 2RA- ^x\ *= (B'O')² — (DO' — BD'f « 2RAr,

о | "1 — V R&h + х~ -f- х_у. (1-62)

поэтому получим I

Из сравнения рис. 1.28 и 1.29 следует, что приращение длины кон­такта за осью валков можно приравнять половине ширины упругого кон­такта цилиндра с плоскостью, т.е. Xi = а. Тогда, согласно уравнению {1.61), получим

Xi ⁼ CRPcv>

¹ -Ип.

(1.63)

х_п + х₁

где С =- 8k_y =

¹— константа упругости валков.

л £

0,3; £ = 2,15-10⁵ МПа; С= 1,08-10 ⁵ мм²/Н.

(1.64)

Для стальных валков ц„ поэтому

х₁ — 1,08-10~⁵ Rp_CIy,

где R выражается в мм и р_ср — в МПа.

В этой формуле р_ср — среднее давление при прокатке с натяжением или без натяжения, определенное также с учетом влияния упругого сплющивания валков. Из рассмотрения формул (1.62) и (1.63) следует, что увеличение длины зоны деформации тем больше, чем больше диаметр валков и дав­ление при прокатке. Интересно отметить, что приращение дли­ны зоны деформации вследст­вие упругого сплющивания валков зависит не от твердо­сти поверхности валков, а от модуля упругости их материа­ла: чем больше Е [меньше ко­эффициент С в формуле (I.63)J, тем меньше упругое сплющи­вание. Модуль упругости для всех сталей почти одинаков (около 2,1—2,2-10³ МПа), чу­гуна в два раза меньше ( ~ 1X Х10⁵ МПа), а для твердых сплавов (например, карбида

Рис. 1.30. Схема равномерной дефор­мации металла в валках при прокатке: а — эпюры скоростей течения металла в различных сечениях зоны деформа­ции; б — изменение горизонтальной составляющей окружной скорости вал­ка V

металла

горизонтальной скорости _хм в зоне деформации

вольфрама) в 2,5—3 раза больше (~6,5-10⁵ МПа). Поэтому при про­чих равных условиях упругое сплющивание чугунных валков будет в два раза больше, а валков из твердых сплавов в 2,5—3 раза меньше, чем сплющивание стальных валков.

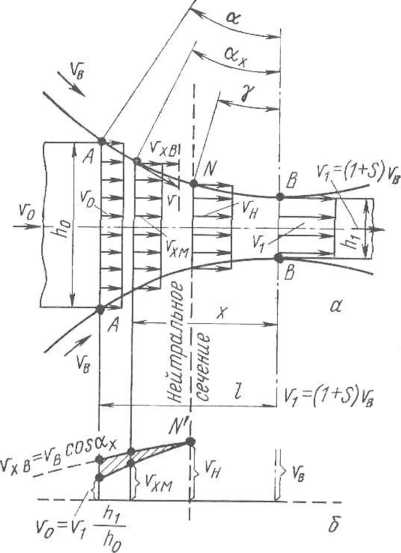
Опережение и уширение металла при прокатке

Выше было указано, что при пластической деформации объем металла не изменяется, изменяются только его форма и размеры. Следователь­но, объем металла, проходящего в единицу времени (Q, мм³/с) через любое вертикальное сечение зоны деформации является величиной по­стоянной.

Предположим, что через сечение входа металла в валки (рис. 1.30) (сечение АА) в секунду проходит Q₀ мм³ металла, а через сечение вы­хода (сечение ВВ) — Q, мм³. Очевидно, что

Qo = Ql = Qx = const. (1.65)

3. 

   33

   А. А. Королев

Это равенство выражает постоянство секундного расхо- д а металла в любом сечении х — 0-+1.

Если предположить, что в любом вертикальном сечении на расстоя­нии х от оси валков скорость течения металла является постоянной и все волокна металла по высоте этого сечения получают одинаковую вы­тяжку, то такая деформация называется равномерной. Тогда Qo=FoVo, a Q\ = F\Vi и, следовательно, можно написать

F₀ v₀ = F₁v₁ = F_x v_x = const, (1.66)

где Fo, F\ и F_x — площади поперечных сечений полосы до входа в вал­ки, на выходе из валков и в сечении х; v₀, V\ и v_x — средние скорости входа металлов в валки, выхода из них и в сечении х.

Из рассмотрения уравнений (1.66) и (1.45) следует, что

Uo/i/j = 1 /Я, (1.67)

т. е. отношение скоростей входа и выхода металла обратно пропорцио­нально отношению площадей поперечных сечений полосы (т.е. X).

Зная скорость выхода металла из валков и вытяжку полосы за дан­ный пропуск, можно легко определить и скорость входа полосы в валки (и наоборот), пользуясь соотношениями

v₀ = vJ'K; v_x ~ Я. (1.68)

Так как Я>1, то v₀<Vi, т.е. скорость входа металла в валки меньше скорости его выхода из валков.

Практика и опыты по прокатке различных металлов показывают, что скорость выхода металла из валков Ui несколько больше, а скорость входа у₀ меньше окружной скорости вращения валков v_B, т.е. Vi>v_B> >v₀.

Металл движется в направлении прокатки горизонтально, а точки на поверхности валка — по окружности со скоростью и_в- Значит, есть такое сечение, в котором средняя скорость металла равна горизонтальной со* ставляющей окружной скорости вращения валков v_XB.

Средние по высоте сечений скорости движения металла выражаются кривой v_XM, a v_XB — косинусоидой u_Bcosa_x (см. рис. 1.30). Точка N ха­рактеризует положение нейтрального сечения, в котором средняя ско­рость металла равна горизонтальной составляющей окружной скорости валков.

Где же расположено нейтральное сечение, которое делит всю область деформации на две зоны: зону отставания и зону опережения. Вопрос этот весьма сложный, и пока еще невозможно дать точное математичес­кое определение положения нейтрального сечения. Приближенно, но с очень небольшой ошибкой, этот вопрос решается следующим образом.

Предположим, что давления распределяются по дуге захвата равно­мерно, т.е. величина их постоянна от точки входа А к точке входа В, что вполне допустимо для случая горячей прокатки. В зоне отставания (дуга AN) и в зоне опережения (дуга NB) на бесконечно малый элемент дуги захвата, равный Rdq>, действует радиальная (нормальная) сила dN=pRd(p и тангенциальная сила трения dT = pnRd(p, где d(p — беско­нечно малый угол в любой части зоны деформации (рис. 1.31). Сумма горизонтальных проекций этих элементарных сил при принятом напра­влении осей координат равна

• hpRdy sin ф — 'ZpyiRd cp cos cp;

2Хдгв — sin ф + 2р|л£$ф cos ф.

Так как металл движется равномерно и на него не действуют ника­кие другие силы, кроме сил N и Т, то из условия равновесия сумма го­ризонтальных сил слева и справа от нейтрального сечения должна быть равна нулю.

Для зоны отставания угол ф изменяется от величины угла у до вели­чины угла захвата а; для зоны опережения угол ф изменяется от нуля до величины угла у, определяющего положение нейтрального сечения.

Сокращая правую и левую части на pR и заменяя суммирование интег­рированием по переменному углу ф, получим

а V

j (sin ф — fx cos ф) ^ф 4- j* (sin ф + |Л cos ф) ^ф = 0.

у 6

Проинтегрировав и подставив пределы изменения угла ф, получим (формула Экелунда — Павлова)

sin a sin² а/2 а /. а \ _{/т СП}\

sm-y = ; у «— 1 . (1.69)

ц 2 \ 2(х

Из этой формулы следует, что положение нейтрального сечения оп­ределяется для данного угла захвата величиной коэффициента трения:

Ряс. 1.31. Силы, дейст­вующие на металл в зоне отставания AN и н аове опережения NR при установившемся процес­се прокатки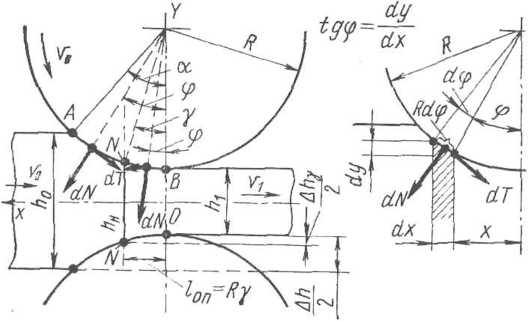

чем больше коэффициент трения, тем больше величина нейтрального угла и тем больше нейтральный угол приближается к середине дуги зах­вата.

При выводе этой формулы не учитывалось влияние уширения поло­сы на положение нейтрального сечения. Однако, как показывают более подробные исследования, для обжатий e = 0,20-f-0,40 это влияние незна­чительно; поэтому можно считать, что формула (1.69) и в этом случае пригодна для подсчета опережения и угла у.

Скорость выхода металла из валков Ui (скорость прокатки) больше окружной скорости вращения валков v_B — это явление называется опе­режением металла при прокатке.

Обычно опережение определяется как относительная величина (без­размерная, в сотых долях или процентах), т.е. как отношение разности скоростей Vi и v_B к окружной скорости валков v_a

s = (v₁ — v_B)/v_B = v₁lv_B~\. (1.70)

Теоретически опережение определяется следующим образом (без уче­та уширения).

В нейтральном сечении горизонтальная скорость движения металла равна горизонтальной составляющей (проекции) окружной скорости валков v_M = u_B cosy (рис. 1.30). Из условия постоянства секундного рас­хода металла в любом вертикальном сечении зоны деформации Q = = v_Mh_H — Vn cosyh_H = Vihi = const имеем vi/v_B = h_a(cosy/hi).

Из рис. 1.31 следует, что

• К + ² (ДА? /2); R — R cos у = Ahy /2;

h_e = h₁ + 2R(l- cos у) ж h_t + 2R 2 sin² (у/2) tth_x + Ry², поэтому

vJv_K -- (h_x 4- Ry²) (cos y/h_x) « I -\- RyVh_x.

Подставляя это значение в формулу (1.70), получим

s = (R/h₁)y². (1.7 J)

Таким образом, опережение тем больше, чем больше радиус (диа­метр) валков и меньше толщина полосы. Кроме того, опережение про­порционально квадрату нейтрального угла у (в радианах). Так как, со­гласно формуле (1.69), нейтральный угол увеличивается с ростом коэф­фициента трения, то увеличивается и опережение (по еще в большей сте­пени). Как показывает более подробный анализ и практические данные с увеличе­нием ширины полосы опережение также увеличивается.

Рис. 1.32. Измерение опережения при помощи кернов на валке

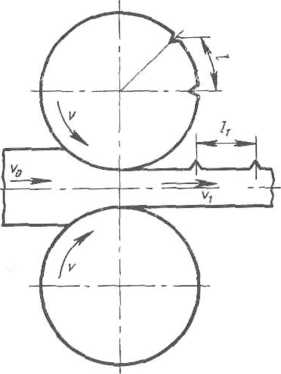
Наиболее простым, практическим ме­тодом определения опережения является так называемый метод к е р н о в, кото­рый заключается в следующем. На по­верхности валка при помощи керна дела­ют углубления на расстоянии I друг от друга (например, 100 мм), которые остав­ляют отпечатки (выпуклости) на полосе после прокатки (рис. 1.32). Вследствие того, что металл выходит из валков со скоростью V], которая больше окружной скорости валков расстояние между кернами на полосе i_t больше расстояния I на валке. Величина опережения в этом случае определяется по формуле

s = 100 %. (1.72)

Обычно опережение составляет 3—8 %.

При обжатии металла в валках по высоте большая часть его дефор­мируется в длину (удлинение, вытяжка), а небольшая часть в ширину (уширение вдоль бочки валков), поэтому ширина полосы увеличивается (b_l>b_Q).

Абсолютное уширение (приращение ширины) можно опре­делить по формуле автора

АЬ^Ь, — 6₀= (1.73)

1 — £

Из этой формулы следует, что уширение пропорционально протяжен­ности зоны опережения l₀n~Ry- Таким образом, факторы, увеличиваю­щие опережение (увеличение диаметра валков, коэффициента трения, обжатия и уменьшение толщины полосы), также увеличивают и ушире­ние. При прокатке широкой полосы уширение незначительно и во многих случаях его можно не учитывать.

Коэффициент трения и скорость деформации

Коэффициент трения. Выше было указано, что процесс прокатки возмо­жен только при наличии трения между металлом и валками и что поэ­тому контактные силы трения в данном случае полезны. Однако из это­го следует делать общий вывод, что чем больше коэффициент трения, тем лучше будет проходить процесс прокатки. Из приведенного выше анализа следует, что чем больше коэффициент трепия, тем больший угол захвата (а значит, и большее обжатие металла) можно допустить при прокатке. Условия захвата являются решающими только тогда, когда применяются большие абсолютные обжатия (например, при горячей прокатке блюмов, заготовки и т.д., когда делают насечку валков), и эти обжатия не влекут за собой значительного увеличения давления на валки и не вызывают их поломки. Но во многих случаях прокатки, например при горячей и холодной прокатке листов, процесс прокатки ограничивается не максимальным обжатием и коэффициентом трения, а допустимым давлением металла на валки (которое при прокатке тонких листов бывает очень большим). В таких случаях необходимо стремиться

к уменьшению коэффициента трения, для чего применяют шлифован­ные валки, а также смазки ух и полосы во время прокатки.

Истинное значение коэффициента трения при прокатке определить экспериментально довольно трудно, так как величина коэффициента трения зависит от состояния поверхности валков, их смазки, давления и температуры при прокатке, скорости прокатки и т.д. Известные в ли­тературе методы дают косвенное определение этого коэффициента для каждого конкретного случая прокатки.

При горячей прокатке полосы и профилен коэффициент трения (л можно определить по формуле Экслунда

и = /2,(1,05 — 0,00050 (^т-⁷⁴)

где i — температура металла при прокатке, °С; П\ — коэффициент, ха­рактеризующий состояние поверхности валков; для стальных валков с грубой поверхностью ti= 1, для чугунных валков с закаленной поверх­ностью «1 = 0,8; п₂ — коэффициент, учитывающий скорость прокатки, при и =1,5; 10; 15; и 20 м/с можно принимать соответственно /гг =1,0;

1. 9; 0,8; 0,75 и 0,7.

Формула (1.74) справедлива для />700°С. Из этой формулы следу­ет, что с увеличением температуры и скорости прокатки металла коэф­фициент трения уменьшается.

При холодной прокатке листов и полосы можно пользоваться следу­ющими значениями коэффициента трения, полученными измерением опережения и подсчетом по формулам (1.69) и (1-71):

При прокатке тонкой стальной полосы жести на шлифованных валках с весьма хорошей смазкой полосы:

пальмовым маслом 0,03—0,04

эмульсией пальмового масла 0,05—0,065

/IV.1 1

КОНСТРУКЦИЯ И РАСЧЕТ МАШИН И МЕХАНИЗМОВ ПРОКАТНЫХ СТАНОВ 2

fcr'c-Hl- 47

-^ = 4-! 52

1_С — х_г V RAh + xi 1 I' -I- xi ; I' - 2xi l_z =-- i²; 56

T ⁼ (^,+ii)ⁿ->^{: (П}-^21а) 62

. г' 96

Й-Г. + Й»-70^(7- + -^-). (III.45) 162

I* ?(*■ 206

j ■ 1: 245

L — ^ ^ j L_0CH = ^ 2 L_0CH ⁼ j 2 ^{= MM}" 280

+-И(И* 352

№ № 355

^Ht)4 399

При прокатке тонких стальных листов и полосы на шлифованных пал­ках с хорошей смазкой:

эмульсией минерального масла 0,07—0,1

эмульсией пальмового масла или его заменителем (касторового мас­ла п др.) 0,06—0,08

При дрессировке листов и полосы на шлифованных валках всухую (без

смазки) 0,12—0,15

Меньшие значения коэффициента трения соответствуют скорости свыше 5 м/с, большие — скорости до 5 м/с. При прокатке цветных ме­таллов коэффициент трения на 10—20 % больше, чем при прокатке стали.

Скорость деформации. Как было сказано выше, скорость деформации существенно влияет на предел текучести металла (или сопротивление чистому сдвигу) в процессе его деформации; с увеличением скорости деформации сопротивление деформации а_д возрастает, особенно при не­больших и средних обжатиях (к<30 %).

Скоростью деформации называется производная относительной деформации е по времени, т. е.

и = dzldt. (1-75)

Следует обратить внимание, что в отличие от линейной скорости де­формирования, выражаемой в м/с или мм/с, скорость деформации имеет размерность 1/с.

Скорость деформации металла в условиях его обжатия при прокатке определим следующим образом.

Относительное обжатие металла в любом сечении на расстоянии х от оси валков, согласно формуле (1.42), можно представить как (рис.

1. 33): е*= [hx—h\)jh_x=Ah_xfh_x, где !г_х и А1г_х— текущие значения высоты сечения и его абсолютного обжатия.

Для бесконечно малых деформаций это выражение имеет вид с1г =

= dhxfhx, поэтому скорость деформации металла в сечении х можно выразить через

и_х == (dhjdt)(\/h_x) - 2vjh„ (1.76)

где dhxldt = 2v_y — линейная скорость деформации элемента металла в направлении высоты h< (т.е. в вертикальном направлении сжатия ме­талла), осуществляемой двумя валками, м/с или мм/с.

Рис. 1.33. К определению скорости деформации (а) и изменение ее по длине контакта при про­катке (б)

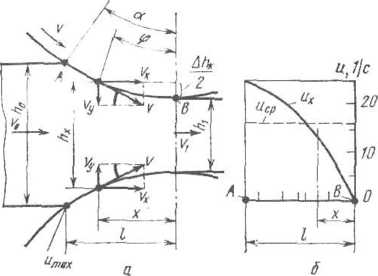
Согласно рис. 1.33 и уравне­нию постоянства секундного объ­ема деформируемого металла (1.66) можно определить верти­кальную скорость сжатия метал­ла в сечении х зоны деформа­ции:

v_v = v_x tg q> = (v, h_ylh_x) tg q>.(1.77)

Построенная по формулам (1.76) и (1.77) кривая изменения скорости деформации и_х по дуге захвата показывает, что при h_x — hо и т. е. в нача­

ле дуги захвата (точка А), ско­рость деформации является мак­симальной; по направлению к вы­ходному сечению скорость дефор­мации резко уменьшается и в самом сечении выхода при ф = 0 она рав­на нулю.

Для учета влияния скорости деформации на повышение предела те­кучести деформируемого при прокатке металла в дальнейшем для оп­ределения давления металла на валки нас будет интересовать средняя скорость деформации по длине контакта /, равная средней ординате

на этой длине: u_cp = — ('u_xdx.

1. о

Подставляя и_х по уравнению (1.76) и учитывая, что tgcp = dh_x/2dx₁ получим

А. vthi /' dhK vtkt
1 J Ai Z	hx h0

Так как Но—/ii = A/i = e/io = a/, то получим следующую расчетную формулу

u_cv> - е (vjl) a (v_x/h_Q), (I.78)

где V\—скорость выхода металла из валков; a—угол захвата, рад; е — относительное обжатие.

Таким образом, скорость деформации пропорциональна скорости про­катки, обжатию и обратно пропорциональна длине зоны деформации.

Следует отметить, что влияние скорости деформации проявляется в значительной степени только тогда, когда температура деформации вы­ше температуры рекристаллизации металла, т.е. при горячей прокатке. При холодной прокатке металла с небольшими и средними скоростями (vi<15 м/с) скорость деформации весьма незначительно влияет на да­вление металла при прокатке и расход энергии. Это влияние можно не учитывать. В этом случае надо учитывать упрочнение (наклеп) металла при его обжатии в валках (см. рис. 1.15).

Коэффициент полезного действия процесса прокатки

Потери энергии (мощности) при прокатке являются следствием наличия относительного контактного трения — скольжения на протяжении дуги захвата (см. рис. 1.30).

Скорости скольжения определим следующим образом: в сечении входа металла в валки

I s

'в '

Ь»л = о_в-

A. cos а

cos а Я cos а

в нейтральном сечении Al’_h —0; в сечении выхода металла из валков Av_B=v_x—ub=i'_b(1+s)—v_b=VbS (см. с. 33). В зонах отставания и опе­режения скорости скольжения Ди₀т и Av_on противоположны по направ­лению, но они вызывают один и тот же эффект — потерю энергии на трение скольжения (нагрев металла и валков); принимая прямолиней­ное уменьшение Av от сечения входа и сечения выхода по направлению к нейтральному сечению, получим среднее суммарное значение скоро­сти скольжения для всей зоны деформации

1 +s

A cos а

JY ^а / „

Y \2 а

До.

Av,

(а — у) -f

1 —

+

2 9 F

7—

1 — е

(1.79)

где принято (см. с. 35)

ДА

rd

V \²

а )

г

Л,

hx

1 — е

1

и — 2

(см. с.

При граничных значениях нейтрального угла (— ) О;

35) получим, соответственно, Ди_Ср/ив=0,5е; 0,36е и я^0,27е. С достаточ­ной для практических расчетов точностью можно принять следующие значения Av_Cp/v: для (7/а) =0-r-0,25Au_cp/u = 0,43e; для (у/сс) = 0,25-г-

ч-0,5Ди_ср/ул = 0,31е. Например, при е=0,25 получим, соответственно, Av_cp/v_B=0,\\ и 0,077, т.е. в среднем около 9% от окружной скорости валков.

Мощность потерь на трение скольжения для всей зоны деформации при т~ const и ширине полосы Ь=\ составляет Л^_тр = 2тга(ДУср).

2-Чи_в.

а

Мощность прокатки (мощность деформации на бочках двух валков (см. с. 45).

yV_np — 2М_ПР со_в 2тга I 1

Коэффициент полезного действия процесса прокатки

/V

_ '^vnp

тр __ |

CP

(1.80)

тр |

Л =

N

N

пр

пр

^}в 1—2 (у/а)

До,

Например, для (7/а) = 0-f-0,25 при е^0,25 получим г)_с1>=1—0,6е« ^0,85, т. е. 85% (15% составляют потери на нагрев металла и вал­ков). Из анализа формул (1.79) и (1.80) следует, что к. п. д. процесса прокатки уменьшается при увеличении обжатия и отношения у/а.