
- •Королев а. А. Конструкция и расчет машин и механизмов прокатных станов:
- •Андреи андреевич королев конструкция и расчет машин и механизмов прокатных станов 2-е изд.
- •Часть первая теория расчета давлений, усилий и мощности при прокатке
- •Глава I. Основы теории обработки металлов давлением и теории прокатки . .
- •Глава II. Давление и усилие на валки, моменты и мощность прокатки
- •Глава IV. Привод валков рабочих клетей
- •Часть третья режущие машины
- •Глава V. Ножницы с параллельными ножами
- •Глава IX. Лнстоправильные и сортоправильные машины .... 295
- •Глава I.
- •Элементы теории напряжений
- •2. Механические схемы деформации
- •Пластическая деформация металла
- •Основные расчетные параметры процесса прокатки
- •V,. Град
- •Глава II.
- •Давление при равномерной деформации металла
- •Давление при неравномерной деформации металла
- •Влияние натяжения полосы при холодной прокатке
- •Влияние упругого сплющивания валков при холодной прокатке
- •Влияние внешних зон
- •Давление на валки при прокатке сортовых профилей
- •Измерение давления металла на валки при прокатке
- •Простой процесс прокатки
- •Прокатка на стане с холостым валком
- •Прокатка на стане с валками неравного диаметра
- •Прокатка полосы с натяжением
- •Прокатка на многовалковом стане
- •Момент и мощность прокатки
- •Проверяем наличие зоны прилипания на дуге захвата а:
- •Определяем среднее давление металла на валки и полное усилие прокатки:
- •Проверяем наличие зоны прилипания по формуле (II.18а):
- •Находим длину контакта без учета влияния упругого сплющивания валков
- •Определяем среднее давление металла на валки с учетом натяжения полосы.
- •Определяем полное усилие прокатки:
- •Определяем длину контакта и среднее давление с учетом упругого сплющивания валков при прокатке без натяжения:
- •Определяем длину контакта и среднее давление с учетом упругого сплющивания валков при прокатке с натяжением:
- •Находим полное усилие прокатки с учетом упругого сплющивания валков:
- •Усилия на 1 мм ширины бочки валка и среднее давление согласно формулам (II.25а) и (н.25г) для п.П.1, 2 и 3 соответственно равны:
- •Находим величины:
- •Находим величины:
- •Определяем полное усилие прокатки
- •Определяем:
- •Находим полное усилие прокатки
- •То же, с учетом упругого сплющивания валков:
- •Определяем момент при прокатке полосы без натяжения:
- •При прокатке полосы с натяжением момент прокатки (момент на бочке валков) значительно меньше, чем при прокатке без натяжения.
- •Проверка двигателя по моменту.
- •Проверка двигателей по мощности.
- •Определяем момент прокатки
- •Находим статическую мощность двигателей другим способом — по удельному расходу энергии.
- •Поясним данные, приведенные в табл. II. 1.
- •Поясним данные табл. II.1 применительно к нагрузочной диаграмме, приведенной на рис. 11.29.
- •Глава III.
- •Подшипники и подушки валков
- •Механизмы и устройства для установки и уравновешивания валков
- •Рабочие клети прокатных станов
- •Глава IV.
- •Шпиндели
- •Максимальное усилие в зубчатом зацеплении рассчитаем по формуле (IV.26)
- •Глава V.
- •Назначение и основные параметры
- •Ножницы с эксцентриковым плавающим валом
- •Глава VI.
- •Классификация и назначение
- •Глава VII.
- •Назначение
- •Глава Vlfl.
- •Барабанные летучие ножницы
- •Кривошипно-шатунные летучие ножницы
- •Глава IX.
- •Назначение и классификация листоправильных машин
- •3. Методика расчета рабочих и опорных роликов
- •Конструкция
- •Глава X.
- •It]* 205-0.984 Номинальный момент электродвигателя
- •Перспективы развития прокатных станов
- •6. Рассчитываем полное усилие прокатки:
- •2. Тангенциальное напряжение на внутренней поверхности втулки по формуле Ляме
- •2. Находим статический момент резания.
- •1 Определяем среднее давление металла на валки по формуле (II.21а)
Для
анализа процессов обработки металлов
давлением применяют так называемые
механические схемы деформации; каждая
такая схема состоит из двух схем:
схемы главных напряжений и схемы главных
деформаций.
В
качестве примера на рис. 1.9, приведены
механические схемы деформации.
При
прессовании (выдавливании через очко
матрицы) металл находится в напряженном
состоянии всестороннего сжатия (все
три главные напряжения а — сжимающие):
в направлении оси цилиндрического
контейнера
происходит деформация удлинения, а
по двум другим осям — деформация сжатия
(рис. 1.9, а).
При
волочении схема напряженного
состояния разноименная: по оси
протягиваемого прутка действует
напряжение растяжения, по двум другим
осям — напряжения сжатия (давления со
стороны волоки). Схема деформации
аналогична схеме деформации при
прессовании (рис. 1.9,6).
При
прокатке и осадке металла вследствие
наличия контактных сил трения схема
напряженного состояния аналогична
схеме при прессовании, т. е. всестороннее
сжатие; схема деформации состоит из
одной деформации сжатия (обжатие
металла по толщине) и двух деформаций
удлинения (по длине и ширине), рис. 1.9,
в.
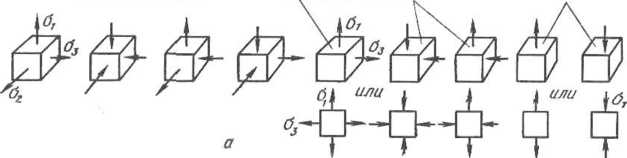
Всего
имеется девять схем напряженного
состояния и три схемы деформированного
состояния; сочетание их позволяет
получить более 20
механических
схем деформаций (рис. 1.10).
/
/
Рис.
1.9. Схемы напряжений и деформаций:
Объемные
схемы
Плоские
схемы
\£Г
1
П
Рис.
1.10. Механические схемы деформаций:
Линейные
схемы
б,
/
£<
Ш
с.
£гУ~
напряженного
состояния; деформированного состоя-
а
— схемы б
— схемы ния


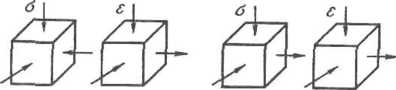



![]()

![]()









2. Механические схемы деформации
Для того, чтобы определить, по какой схеме предельного напряженного состояния происходит пластическая деформация металла, пользуются следующим приемом: в зоне деформации металла мысленно выделяют бесконечно малый кубик (объем) металла, грани которого подвержены действию главных нормальных напряжений.
Главные
нормальные напряжения, действующие на
грани кубика, обозначают через oi,
02
и <73
и называют: Oi
— максимальным; 03
— минимальным и <т2
— средним (по величине между о\
и сг3) напряжением.
Схемы объемного напряженного состояния: всестороннее растяжение, всестороннее сжатие и две разноименные схемы.
Схема всестороннего растяжения является самой невыгодной схемой деформации, так как очевидно, что металл при этом обладает малой пла
стичностью. Практически при обработке
металлов давлением эту схему не
применяют,
а ее используют только при растяжении
образцов,
имеющих
местное сужение (шейку), т.е. при растяжении
образцов переменного сечения.
Очевидно, что по схемам всестороннего
равномерного W1
=сг2=а3)
сжатия или растяжения деформация
невозможна. Все процессы обработки
металлов давлением построены по схеме
всестороннего неравномерного сжатия
[оуфоъфоъ)
или по разноименным объемным схемам
(сжатие — растяжение).
Схемы плоского напряженного состояния — это схемы, в которых одно из главных напряжений равно нулю. Таких схем три: двустороннее растяжение, двустороннее сжатие и разноименная схема (растяжение — сжатие).
Схемы линейного напряженного состояния (простое растяжение или сжатие). Линейная схема применяется при испытании образцов постоянного сечения на растяжение. Линейные схемы сжатия практически неосуществимы, так как контактные силы трения на плоскостях сжатия создают горизонтальные напряжения в металле, и фактически при этом получается объемная схема сжатия. Только по краям образца, где влияние сил трения незначительно, условно можно считать, что металл находится в напряженном состоянии линейной схемы сжатия (рис. 1.11).
Р\
////////А/////{/л
Рис.
1.11. Влияние контактного трения на
напряженное состояние металла в
середине н по краям заготовки при
осадке ее (F
—
силы трения)
%
1
%
1
/у
V4
ФЮ
Рис.
1.12. Влияние схемы напряженного состоя-
вня металла на сопротивление его
деформации при волочении и выдавливании
(по С. И. Губкину)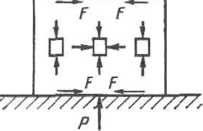
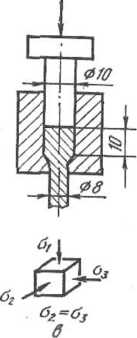
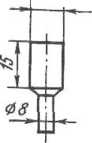
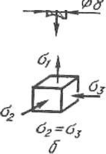





Поясним значение и влияние различных схем напряженного состояния следующим весьма наглядным опытом С. И. Губкина.
Медный отожженный образец (рис. 1.12, а) закладывали в матрицу (рис. 1.12,6) и к нижнему концу его прикладывали растягивающее усилие, т. е. осуществляли процесс волочения. Когда высота образца в матрице с 15 мм уменьшилась до 10 мм, усилие волочения по прибору было равно 10,5 кН. В этот момент опыт прервали и вместо растягивающего усилия приложили сжимающее усилие, для чего поместили в матрицу пуансон (рис. 1.12,5) и нагрузили его сверху. Таким образом опыт продолжали при осуществлении процесса истечения металла (процесса прессования) через очко. Для того чтобы металл опять начал течь при этом способе, к пуансону потребовалось приложить сверху усилие, равное 35,3 кН, т. е. значительно большее, чем при волочении.
Главные нормальные напряжения при этом были равны: при волочении
ctj
= pip
= (10500*4)/(я-82) - 220 МПа; при прессовании
=
P/F= (35300-4)/(я- Ю2) = 450 МПа.
И в этом и в другом случае были так называемые объемные схемы напряженного состояния, т. е. на металл действовали три взаимно пер-
пендикулярных
главных напряжения: oi, о2
и аз- Однако при волочении одно из этих
напряжений было растягивающим
(разноименная схема), а при прессований
все три были сжимающими. Таким образом,
повышение приложенных внешних усилий
(с 10,5 до 35,3 кН) и давлений (главных
нормальных напряжений tii)
произошло исключительно вследствие
изменения схемы напряженного состояния
металла в рабочем пространстве при
деформации. В обоих случаях механические
свойства металла были неизменными,
однако сопротивление деформации
изменилось.
Таким образом, можно сделать вывод, что сопротивление деформации и пластичность металла — это не свойства его (как, например, предел текучести), а состояние; они зависят не только от природы его, но и от схемы напряженного состояния.
В каждой точке деформируемого тела имеются три взаимно перпендикулярных направления, которые являются главными осями деформаций; по направлению этих осей деформируемое тело испытывает главные линейные деформации еь ег и е3 (сжатия или растяжения).
.. ПРИ пластической деформации объем металла не изменяется, т. е. V=const и приращение объема равно нулю (ДУ=0). Если длину ребра исходного кубика металла принять равной единице, то можно записать *
AV
= (1 -f- 8])
(1
+ е2)
(1 +63)
— I л? -f- ®2
4' ез =
0» (1.236)
Ьг
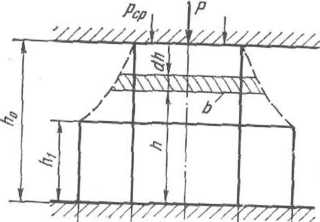
Рис.
1.13. К определению истинной (логарифмической)
деформации при осадке металла
Например,
ири прокатке широкого листа уширением
можно пренебречь (е2
= 0)
и считать, что схема деформации
является плоской (/); при прокатке
толстой заготовки (слитка) прямоугольного
сечения металл обжимается по толщине
(сжатие), а ширина и длина его
увеличиваются (растяжение — схема //,
объемная). При выдавливании и волочении
металла через коническую матрицу (очко)
имеются две деформации радиального
сжатия и одна деформация осевого
растяжения (схема 111,
объемная).
При обработке давлением (прокатке, ковке, прессовании) размеры деформируемого металла изменяются значительно, т. е. имеют место большие пластические деформации. В этих случаях истинную относительную деформацию более правильно определять как интеграл отношения бесконечно малых приращений деформаций (за короткие промежутки времени) к текущей толщине металла, например, для осадки метала по высоте (рис. 1.13) (считая деформацию положительной)
ho
8Л= Г— =1п-^- = !п — =— 1п(1— elssefl + —). (1.23в)
J
ft hi
1
— е \
2 )
hi
Таким
образом истинная (логарифмическая,
интегральная) деформация больше
относительной деформации 6л
>г. Однако при е=0,2 6н>г
только
на 10%,
поэтому на практике при выполнении
различных расчетов чаще применяют
более простые выражения относительного
обжатия через е.
Для
создания условии, необходимых для начала
пластической деформации при различных
схемах напряженного состояния, требуется
приложить к металлу различные по величине
главные нормальные напряжения оь
02
и аз-
При
простом линейном сжатии (растяжении)
(см. рис. 1.3) к металлу надо приложить
со стороны рабочего инструмента (штампа)
вертикальное напряжение 01
= 0^,
равное, согласно формуле (1.7), oi
= oa.
При плоском напряженном состоянии (о2=0) (см. рис. 1.4) в деформируемом металле, согласно формулам (1.12) и (1.22), надо создать разность главных нормальных напряжений, равную ai—Оз = сТд.
В
тех случаях, когда деформация происходит
в условиях объемной схемы напряженного
состояния (т. е., когда имеются все три
главных напряжения о-,,
о2
и ст3), определить условия начала
пластической деформации более сложно.
В отличие от прежних теорий Треска и Сан-Венана, в настоящее время этот вопрос решается на основании так называемой энергетической теории предельного состояния деформируемого материала (теории Губера — Генки — Мизеса), согласно которой пластическая деформация возможна только тогда, когда в упругом материале будет накоплена определенная энергия, необходимая для изменения формы (а необъема) этого материала независимо от схемы напряженного состояния.
Пластическая деформация начнется только после упругой деформации. Потенциальную энергию упругой деформации А можно разделить на две части:
Л = А0 4- (1-24)
где
Ао — потенциальная энергия, направленная
на изменение объема (как известно, при
упругой деформации растяжения объем
тела увеличивается, а плотность
уменьшается); А$
— потенциальная энергия, направленная
на изменение формы тела.
При объемной схеме напряженного состояния металла упругая деформация его происходит в трех направлениях («ь е2 и е3) и полная (удельная) потенциальная энергия, согласно закону Гука, выражается уравнением
А
=
V, fa ех + сг2е2
+ <т3
е3). (1.25)
Так как относительные деформации по закону Гука равны
ех = t/e [ах — ц (сг2 -h сг3)1;
е2 = Vje[cf2— H-fo + tfa)!; (1.26)
е3 = Че [ст3 — И- (а* +
то, согласно уравнению (1.25), получим следующее выражение для полной потенциальной энергии деформации ,
А = ЧгЕ [<j\ + of -f of — 2\i (Oj а2 -f сг2 <т3 + о3 а,) ]. (1.27)
Относительное приращение объема тела при упругой деформации равно сумме деформаций в трех взаимно перпендикулярных направлениях, т. е.
AVIV = ех + е2 -f- е3 = [(1 — 2р)/£] (ах -j- о2 о3), (1-28)
где
ц — коэффициент Пуассона деформируемого
материала; Е
— модуль упругости материала.
Потенциальная энергия, направленная на изменение объема, равна половине произведения относительного приращения объема на среднее напряжение, т. е.
А,
= —
— °1
+ <,г+аз
= 1—^
(а, + а2 + (Tg)1. (1.29)
V 3 6Е
Пользуясь уравнениями (1.27) и (1.29), из формулы (1.24) находим, что удельная потенциальная энергия, направленная на изменение формы, будет равна
\ = А “ Л “ [(] + ^)/6£] [(ai - °2)2 + (а2 - стз)2 + (°з - aiY}‘ (Т-30)
На основании многочисленных опытов установлено, что удельная потенциальная энергия, направленная на изменение формы при пластической деформации, является величиной постоянной, не зависящей от схемы напряженного состояния при деформации (зависит только от природы материала, температуры и скорости деформации). Таким образом, при линейной схеме деформации (ot = oy, о2=аа=0) удельная потенциальная энергия, согласно формуле (1.30) будет равна
(1.31)
(1.32)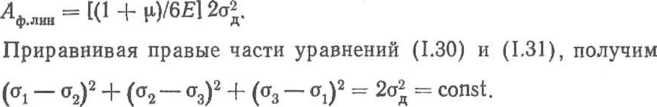
Это так называемое энергетическое уравнение (условие) пластичности в общем виде. Его можно формулировать следующим образом: су м м а квадратов разностей главных нормальных напряжений при объемной схеме напряженного состояния выделенного в металле бесконечно малого элемента есть величина постоянная, равная удвоенному квадрату фактического сопротивления деформации при линейной схеме напряженного состояния.
Применение
уравнения пластичности (1.32) для подсчета
усилий, возникающих при различных
процессах обработки металлов давлением,
осложняется трудностью определения
взаимосвязи между всеми тремя главными
напряжениями oi,
о2
и оз. Однако в этом и нет практической
необходимости, так как основные процессы
обработки металлов давлением можно
свести к двум объемным схемам напряженного
состояния, для которых применение
уравнения пластичности (1.32) значительно
упрощается:
Протяжка и прессование металла через очко (фильер, матрицу). Ввиду того, что деформируемый в очке металл круглого сечения, напряжения в любой горизонтальной плоскости равны между собой, т. е. ог2==Оз. При этом уравнение пластичности (1.32) принимает следующий вид: <Ti—<7з==г Од.
Уравнение (1.32) того же вида, что и уравнения (1.14) и (1.22), полученные из теории максимальных касательных напряжений, согласно которой
'W = СТф/2 = (о-! — 0Г3)/2.
Прокатка. При прокатке широких полос основными деформациями являются высотная (обжатие по высоте) и продольная (удлинение), а поперечная деформация (уширение) незначительна и ею можно пренебречь. Полагая для этого случая относительную деформацию ег (в направлении среднего напряжения сг^) равной нулю (плоская деформация), согласно уравнению (1.26), получим
(1.33)
При пластической деформации (в отличие от упругой) объем деформируемого металла не изменяется, поэтому при ДУ=0 из уравнения (1.29) получим
(1.34)
|х = 0,5.
Таким образом, коэффициент Пуассона при пластической деформации металла есть величина постоянная (так как объем металла не изменяется) и равная ji=0,5.
С учетом выражения (1.34) уравнение (1.33) примет вид:
= (сгх + сг3)/2, (1.35)
т. е. при плоской деформации среднее (по величине) главное нормальное напряжение о2 равно полусумме максимального (0,) и минимального (аз) напряжений.
Такая схема деформации, когда при объемном напряженном состоянии (т. е. существуют все три главных напряжения сгь <j2 и сг3) одна из трех деформаций е* (например, уширение при прокатке) равна нулю, называется плоской (двухмерной) деформацией.
Подставляя условие (1.35) в уравнение (1.32), получим
01_<т3 = (2/J/3) ад « 1,15ад. (1.36)
Ранее (см. рис. 1.5) было установлено, что при чистом сдвиге, когда 0i=—03 (напряжение сжатия равно напряжению растяжения), на наклонной площадке нормальные напряжения будут равны нулю, а касательное напряжение будет максимальным и, согласно формуле (1.17), при а=45° равным
■W = (ai + °з)/2. (!-37)
Сравнивая это выражение с формулой (1.36), получим (при о3 = =—03), что
Ттах = СГд/|^3 « О,580д. (1.38)
Таким образом, мы получим очень важный вывод: максимальная величина, которую физически может достичь главное касательное напряжение при пластической деформации (при чистом сдвиге), равна ~ 0,58 ад и о и а называется константой пластичности.
Напомним,
что по теории максимальных касательных
напряжений (теория Треска и Сан — Венана)
ттах==0д/2
[см. формулу (1.12)]. Увеличение (на 15%)
максимального касательного напряжения
при чистом сдвиге объясняется учетом
влияния среднего напряжения а2
[формула
(1.35)] в энергетическом уравнении
пластичности (1.32).
Уравнение (1.36) в главных напряжениях для плоской (двухмерной)' деформации при объемной сх^ме напряженного состояния имеет вид
01
—03
= k, (1.39)
где
k
= 2тшах - 2/J/3 0Д
« 1,150д.
Уравнение пластичности (1.39) является основным при решении многих задач по обработке металлов давлением и главным образом по прокатке широкой и относительно тонкой полосы. Оно показывает, что при пластической деформации разность главных нормальных напряжений — максимального (01) и минимального (03)—есть величина постоянная, равная удвоенной константе пластичности.
Применяя уравнение пластичности (1.39), надо учитывать алгебраическую, а не абсолютную величину напряжений 01 и 03, т. е. надо учитывать знаки этих напряжений, поэтому более правильно это уравнение записывается так:
(±0i)-(±03)
= К (1.40)
где знак плюс относится к напряжению сжатия (принятому положительным), а знак минус — к напряжению растяжения.
Например, прокатку металла, имеющего фактическое сопротивление линейной деформации 0Д=4ОО и £ = 1,15 04=460 МПа, можно проводить по двум плоским схемам деформации:
а) одноименной схеме сжатия, когда (-fai)=760 и ( + 03) = = 300 МПа (максимальным здесь будет наибольшее по абсолютной величине напряжение сжатия, т. е. oj):
б) разноименной
схеме (сжатие — растяжение), когда (+ori)
=200,
а (—аз) =260 МПа (максимальным здесь
является положительное напряжение oi,
хотя оно меньше по абсолютной величине
чем а3, которое будет минимальным).
Алгебраическая разность в обоих случаях
будет одинаковой, равной k=460
МПа.
Интересно
выяснить, каковы будут напряжения о\
и о3, если при прокатке будет
создана схема напряжений, соответствующая
чистому сдвигу. Очевидно, что этому
случаю соответствует условие равенства
абсолютных величин сч и сг3, т. е.
( + ai) = (—сг3). Подставляя
эти значения в уравнение (1.40), получим
о\
= k/2
—
—сг3, т. е. в рассматриваемом
случае 0^
= 230 и о3
=—230 МПа. Таким образом, при чистом
сдвиге каждое из главных нормальных
напряжений по абсолютной величине равно
максимальному касательному напряжению
(константе пластичности ттах =
=k/2).
Из изложенного следует, что условие начала пластической деформации, определяемое уравнением (1.40), можно обеспечить при двух основных схемах напрялченного состояния деформируемого металла: одноименной схеме сжатия и разноименной схеме сжатие — растяжение; к последней относится и схема чистого сдвига. Так как при обработке давлением (например, при прокатке) нам желательно достичь наибольшего эффекта пластической деформации при наименьших значениях давления [т. е. напряжения cji со стороны рабочего инструмента (валков)], то разноименную схему напряжений следует признать наиболее целесообразной (при деформации пластичных материалов, например стали, допускающих приложение к ним больших растягивающих напряжений а3). Известно, например, что при прокатке полосы с натяжением (растяжением) ее концов моталками требуется значительно меньшее давление валков на металл, чем при прокатке без натяжения.
Выше
было отмечено, что для многих видов
обработки металлов давлением (осадки,
прокатки) нормальные напряжения оу
и ох
на площадках (выделенного бесконечно
малого элемента внутри деформируемого
металла), перпендикулярных осям у
их,
не являются главными, так как на этих
площадках действуют касательные силы
т (например, под влиянием контактных
сил трения, см. рис. 1.11 и II.1).
В таком случае главные нормальные
напряжения (максимальное о\
и минимальное а3) действуют по
площадкам, имеющим некоторый угол
наклона к осям у
и х
(см. рис. 1.6).
Согласно формулам (1.22) и (1.39), получим
—
оxf
+ 4т^
= /г2. (1.41)
Это
есть обобщенное
уравнение пластичности для не главных
напряжений
по осям у
и х,
перпендикулярно которым на площадках
элемента действуют касательные напряжения
Тзсу—Чу*.
Если касательные напряжения значительно
меньше своего максимального значения
при чистом сдвиге {xXy<^k/2),
т. е. если угол между направлениями и о\
(или ох
и аз) незначителен по величине (до 5—10°,
см. рис. 1.6
и пример 2
на стр. 12),
то можно не учитывать их влияние, считать,
что oy=oi,
ох=сг3
и пользоваться уравнением (1.39) в главных
напряжениях.
