Глава I.

ОСНОВЫ ТЕОРИИ ОБРАБОТКИ МЕТАЛЛОВ ДАВЛЕНИЕМ И ТЕОРИИ ПРОКАТКИ

1. Элементы теории напряжений

Все металлы являются кристаллическими телами с правильным распо­ложением атомов в пространственной кристаллической решетке. В на­чале затвердевания жидкого металла образуются кристаллы правиль­ной геометрической формы; при дальнейшем росте они встречаются с со­седними кристаллами и поэтому, несмотря на правильное внутреннее строение, получают неправильную внешнюю форму. Такие кристаллы с неправильной внешней формой (выявленной при травлении шлифован­ных образцов металла специальными химическими реактивами и рас­смотрении их через микроскоп) называются зернами. Вследствие непра­вильной внешней формы зерна соприкасаются друг с другом по лома­ным линиям, видимым в плоскости шлифа; прослойки между зернами способствуют упрочнению соединения зерен друг с другом (рис. 1.1). Опыт показывает, что в результате такого строения металл чаше разру­шается не по границам между зернами, а по самим зернам (по плоско­стям скольжения кристаллов).

Известно, что под действием внешних сил все тела изменяют свои размеры и первоначальную форму или, как говорят, деформируются. Деформация металлов бывает двух видов: упругой и остаточной.

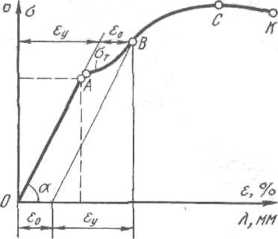
На рис. 1.2 приведен график зависимости напряжения от деформации стального образца при растяжении его увеличивающейся продольной силой. Вначале удлинение образца происходит пропорционально увели­чению нагрузки на него (прямая ОА). Если в этот момент снять нагруз­ку, то образец примет первоначальные размеры и форму. Такая дефор­мация, когда тело после удаления нагрузки принимает прежние разме­ры и форму, называется у п ру го й или обратимой.

В кристаллической решетке атомы занимают такое положение, ко­торое соответствует минимуму потенциальной энергии тела. При упру­гой деформации атомы смещаются из положения устойчивого равнове­сия, причем это смещение очень небольшое и оно не превышает расстоя­ния между соседними атомами. Очевидно, что вследствие увеличения межатомных расстояний объем металла увеличивается, а плотность его уменьшается.

Если увеличивать нагрузку на образец и после достижения упругой деформации, соответствующей точке А, то приращение деформации уже не будет пропорциональным увеличению нагрузки — удлинение образца будет возрастать в большей степени (участок АВ, кривой), чем увели­чение нагрузки, и, наконец, при дальнейшем увеличении нагрузки наступит разрушение (разрыв) образца (точка К). Если не доводя обра­зец до разрыва, снять нагрузку (точка В), то он не примет своих преж­них размеров и формы, а останется несколько растянутым (деформиро­ванным, участок ео).

Такая деформация, при которой тело после снятия нагрузки не воз­вращается к прежней форме и не восстанавливает первоначальных раз­меров, но и не теряет целостности (не разрушается), называется оста­точной (или необратимой, пластической) деформацией. Состоя­ние тела при этом называется пластическим.

Очевидно, что для начала пластической деформации необходимо

преодолеть упругие свойства металла, i.e. сообщить ему упругую де­формацию. Отсюда следует правило: всякой остаточной (пла­стической) деформации предшествует упругая де­формация. Таким образом, при прокатке, например по выходе полосы из валков, размеры ее несколько увеличиваются за счет восстановле­ния металлом своих упругих свойств. Однако, так как упругая деформа-

Рис. 1.1. Схема образования кристаллических Рис. 1.2. Диаграмма растяжения образца из зерен металла (а) и границы между зернами, мягкой иизкоуглеродистой стали видимые под микроскопом (б)

о_в

ция весьма незначительна по своей величине по сравнению с пластиче­ской, то ею обычно пренебрегают, т. е. ее не учитывают.

Основное назначение процессов обработки металлов давлением (ков­ки, прессования, штамповки, волочения, прокатки и т.д.)—пластичес­кая деформация металлов и придание им требуемой формы и необходи­мых размеров. Для этого к металлу прикладывают такое внешнее дав­ление, которое создает в нем так называемые предельные внутренние напряжения, вызывающие изменение формы металла (течение в на­правлении наименьшего сопротивления), но не нарушающие связи ме­жду частицами, т. е. не вызывающие разрушений. При этом атомы сме-‘ щаются на значительные расстояния, превышающие расстояния между атомами в кристаллической решетке, и занимают новое положение ус­тойчивого равновесия. Вследствие этого изменяются также механичес­кие и физические свойства деформируемого металла.

Пластическая деформация возможна только тогда, когда металл об­ладает пластичностью, т. е. способностью деформироваться без разру­шения.

Опыты по растяжению образцов показывают, что деформация проис­ходит путем ряда сдвигов вдоль определенных плоскостей, называемых плоскостями скольжения. При сдвиге этих плоскостей на по­верхности образцов образуются следы, которые называются линиями скольжения. Плоскости скольжения обычно совпадают с плоскостя­ми действия в образцах максимальных касательных (сдвигающих) на­пряжений и составляют с направлением действия внешнего усилия угол около 45°.

Пластическая деформация может начаться только тогда, когда в ме­талле будет создано определенное напряженное состояние. При этом сдвигающие (касательные) напряжения, действующие по плоскостям скольжения, достигнут определенной величины, зависящей от свойств вещества, и будут способны преодолевать внутреннее сопротивление на плоскостях скольжения или по границам зерен металла.

При обработке давлением к деформируемому металлу прикладыва­ют внешние усилия сжатия и растяжения в различных комбинациях. Рассмотрим основные виды деформации и соответствующие им схемы напряженного состояния металла. Здесь и в дальнейшем напряжения сжатия будем считать положительными (знак плюс), а напряжения ра­стяжения— отрицательными (знак минус).

Линейное (простое) сжатие (растяжение)

При сжатии образца осевыми силами Р_у (рис. 1.3) в любом горизон­тальном сечении, имеющем площадь F, возникают нормальные напря­жения, равные

<¹и — PJF. ' (1.1)

Напряжение о_у будет одновременно и главным нормальным напря­жением (обозначаемым 0i), так как в сечениях F, перпендикулярных си­ле Р_у нет касательных напряжений.

Рис. 1.3. Схемы напряжений при линейном (про­стом, одноосном) сжатие

Определим напряжения в лю­бом сечении F\ под углом а к го­ризонтали. Так sFi — s(F/cos а) =

=Fo_y, то, очевидно, вертикаль­ные напряжения s в этом сече­нии будут меньше о_у> т. е. s = o_y'X Xcos а. Выделим внутри дефор­мируемого металла бесконечно малый элемент М (на рис. 1.3 за­штрихован) и рассмотрим усло­вия его равновесия. Разложив s на составляющие: нормальное напряжение о_п (перпендикуляр­ное сечению Fi) и касательное т, получим

о_п = s cos а -- о_у cos² а—(а_у12)^=

^=(1+cos 2а), (1.2)

(1.3)

т = s sin а — а„ sin а cos а =

= (a J2) sin 2а.

На круге Мора напряжения о_п и т характеризуются координатами точки В, перемещающейся по дуге против часовой стрелки. При а = 45° получим

В теории обработки металлов давлением (т. е. при пластической де­формации) под термином «предел текучести» обычно понимают истинное нормальное напряжение (т. е. усилие, отнесенное к площади сече­ния образца в данный момент и приводящее его в пластическое состоя­ние) в процессе однородного линейного растяжения при данной темпе­ратуре с определенной скоростью и степенью деформации. Поэтому ис­тинный предел текучести в теории пластичности следует отличать от предела текучести а_т, применяемого в теории упругости и сопротивления материалов.

(1.6)

С целью использования в дальнейшем имеющихся в справочной ли­тературе данных по пределу текучести различных металлов а_т (при ста­тических испытаниях образцов на растяжение) для условий пластиче­ской деформации фактический (истинный) предел текучести при ли­нейном растяжении (называемый также сопротивлением деформации с_д) можно представить как функцию

<*д =/(М,ы,а_т),

учитывающую влияние степени деформации, температуры металла и скорости деформации.

На основании изложенного выше условие (1.5) будет иметь следую­щий вид:

^mai

(1.7)

Так как на испытательных машинах легче провести испытание об­разцов на растяжение, чем на сжатие (при испытании на сжатие прак­тически невозможно обеспечить линейную схему напряжений ввиду не­избежного возникновения сил трения на контактных поверхностях зажи­мов), то в справочной технической литературе обычно приведены зна­чения от для различных металлов, полученные именно при растяжении образцов. При подстановке этих значений а_т в формулу (I-6) надо иметь в виду, что для некоторых металлов (например, стали) о_т при пласти­ческом растяжении приблизительно на 10 % ниже, чем при сжатии, а для меди и алюминия их значения почти совпадают. Так как пластичес­кая деформация при прокатке осуществляется сжатием металла между валками, то справочные данные по а_т для стали надо в этом случае уве­личивать на 10 % [например, при пользовании формулой (1.6) для оп­ределения среднего давления при прокатке]. Влияние наклепа,темпера­туры и скорости деформации (значения коэффициентов п_а,п_г\\п_и) рас­смотрено ниже.

Сжатие по двум перпендикулярным направлениям (одноименная схема)

Очевидно, что при сжатии по двум перпендикулярным направлениям (рис. 1.4) силы Р_у и Р_х будут создавать на наклонной площадке F\ нор­мальные напряжения а „и а„, направленные в одну и ту же сторону, и касательные напряжения т' и т", направленные в разные стороны. Из условия равновесия выделенного бесконечно малого элемента получим

о_п =а'_п + о'_п = о_уcos²а -f o-_xsin²a = 3-(I -f cos2a) -f

т = т' — т" ^ay~^ax-sin2a,

2

(1.9)

На круге Мора напряжения or_n и т характеризуются координатами точки В. При а = 45° получим .

(U0)

(1.11)

Таким образом, при одноименной плоской схеме (сжатие—сжатие) максимальное касательное напряжение равно полуразности нормальных (главных) напряжений.

Рас. 1.4. Схема напряжений при сжатии по двум перпендикулярным направлениям (одноименная)

Согласно теории Треска и Сан-Венана, максимальное касательное напряжение, необходимое для начала пластической деформации метал­ла, есть величина постоянная, не зависящая от того, по какой схеме (растяжение, сжатие или их комбинация) осуществляется деформация (теория макси­мальных касательных напря­жений). Поэтому, согласно формуле (1.7), можно напи­сать

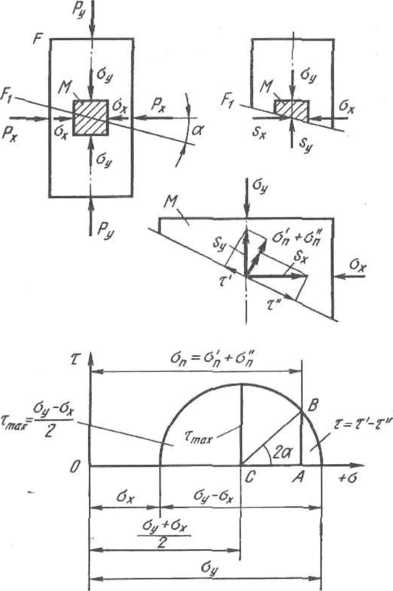
*тах=К—= V² (^{I I2}) или

— = (1.13)

Так как в данном случае нормальные напряжения о_у (максимальное) и о_х (мини­мальное) в поперечных сече­ниях, перпендикулярных силам Р_у и Р_х, являются главными v нормальными напряжениями oi и аз (касательных напряже­ний нет в этих сечениях), то формулу (1.13) можно также представить в следующем виде:

Ci Gg = Од. (1.14)

Из уравнения (1.14) следу­ет, что согласно этой теории, при одноименной схеме напря­женного состояния разность главных нормальных напря­жений есть величина постоян­ная, равная фактическому со­противлению деформации металла, определенному при линейном (про­стом) сжатии.

Сжатие — растяжение по двум перпендикулярным направлениям (разноименная схема)

Очевидно, что при сжатии — растяжении по двум перпендикулярным направлениям (рис. 1.5) силы Р_у и Р_х будут создавать на наклонной площадке Fi нормальные напряжения о_п и о_п', направленные в разные стороны, и касательные напряжения т'и т", направленные в одну и туже сторону:

= °п—^ап = ^{cos2 а}—^а*^{sin2 а} = К—°_ху² +1 (ву + °х)Щ^{cos 2а};

(1.15)

T = T4x'' = ^i^sin2a. (1.16)

На круге Мора напряжения a_n и т характеризуются координатами точки В. При а = 45° получим

■tmax = к + crJ/2 = (<?! + ст₃)/2 = а_д/2, (1.17)

т.е. при разноименной (плоской) схеме напряженного состояния (сжатие — растяжение) максимальное ка­сательное напряжение равно полусумме абсолют-

ных значений главных нормальных напряжений или, что то же самое, алгебраическая разность главных нормальных на­пряжений есть величина постоянная, равная согласно уравнению пла­стичности (1.7), фактическому сопротивлению деформации металла:

tfi —(—о-₃) = а_д. (1.18)

Сравним одноименную и разноименную схему. Предположим, что го­ризонтальное напряжение <7х=о^гз=const. Тогда очевидно, что для на­чала пластической деформации (т. е. для создания в металле определен­ного касательного напряжения ттах=сГд/2) при одноименной схеме де-

Рис. 1.5. Схема напряжений при сжатии — растяжении по двум перпендикулярным на­правлениям (разноименная)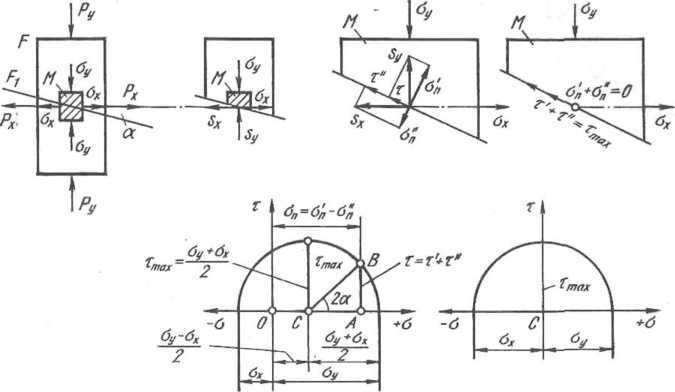

формации потребуется создать вертикальное напряжение G_y=0\ = 0_R-\- + аз, а при разноименной 0_у=0\ = 0д—а₃, т. е. в первом случае о_у боль­ше, чем во втором. Отсюда следует, что разноименная схема деформа­ции более выгодна при обработке металла давлением, чем одноименная, так как она позволяет осуществлять пластическую деформацию при меньших вертикальных давлениях на металл со стороны рабочего ин­струмента (валков, штампа). Известно, например, что при прокатке по­лосы с натяжением (растяжением) ее концов моталками (см. с. 50) тре­буется значительно меньшее давление валков на металл, чем при про­катке без натяжения.

Рассмотрим частный случай разноименной схемы, когда о_у = а_х (по абсолютной величине) и а = 45°. Из формул (1.15) и (1.16) следует, что при этом нормальное напряжение на наклонной площадке будет равно нулю (сгп=0), а касательное напряжение по-прежнему будет макси­мальным и равным Ттах=ст</ = сГх=сгд/2. Этот случай называется чис­тым сдвигом при пластической деформации.

Одноименная (см. рис. 1.4) и разноименная (см. рис. 1.5) схемы на­пряжений называются плоскими, а сама деформация называется плос­кой или двухмерной, так как, согласно теории максимальных касатель­ных напряжений, учитываются напряжения только в двух направлениях (по координатам у их). При этом предполагается, что третья деформа­ция (в направлении оси z, перпендикулярной плоскости ху) равна ну­лю. Фактически в направлении оси z деформация и напряжения не рав­ны нулю — их влияние будет учтено ниже.

Главные направления и главные нормальные и касательные напряжения

При рассмотрении одноименной и разноименной схем напряжений бы­ло принято, что напряжения о_у и и_х являются главными, а касательные

напряжения на вертикальных и горизонтальных площадках отсутствуют и имеются только в наклонных сечениях. В действительности при обра­ботке металлов давлением (например, при осадке, выдавливании, воло­чении и прокатке) имеют место обратные случаи: на вертикальной и го­ризонтальной площадках выделенного в зоне деформации бесконечно малого элемента, кроме нормальных о_у и о_х, имеются также касатель­ные напряжения, причем все эти напряжения не являются главными и максимальными. Таким образом, возникает обратная задача: опреде­лить положение таких наклонных площадок, которые являются главными т. е. нормальные напряжения на них являются главными (макси­мальными cTj и минимальными а₃), а касательные напряжения равны ну­лю (рис. 1.6). При этом напряжении о_у, о_х и т_ху на вертикальной и го-

Рис. 1.6. К определению касательных напряжений при двухстороннем сжатии (плоская схе­ма напряжений)

ризонтальной площадках являются известными (заданными). Из усло­вия равновесия (сумма моментов относительно оси равна нулю), следует, что касательные напряжения на взаимно перпендикулярных пло­щадках равны между собой, т. е. x_xy=i:_yx=-x (первая буква в индексе обозначает направление т, вторая — площадку, перпендикулярную дей­ствующей силе). В соответствии с предыдущими выводами [см. форму­лы (1.8) и (1.9)], получим следующие формулы, характеризующие зави­симость между заданными напряжениями о_у, о_х и т и искомыми главны­ми нормальными напряжениями Oi и а₃ (для одноименной схемы сжатие — сжатие):

W = «.”-^a±^S!- + l/"(-^2lLp^L)^, + t‘ (1.19)

+ т², (1.20)

где т = [(dj — <J₃)/2] sin 2а.

Из круга Мора для данного случая можно определить положение (угол а) главной наклонной площадки, на которой касательные напря­жения равны нулю (рис. 1.6,а):

tg2a = —; a = -i-arctg—. (1.21)

Оу О_х 2 Оу О_х

Хотя выделенный в зоне деформации бесконечно малый элемент с на­клонными гранями не имеет касательных напряжений на этих гранях, это не означает, что внутри него нет касательных напряжений. Из рис.

6. следует, что этот наклонный элемент находится в условиях нерав­номерного сжатия с напряжениями на гранях Oi и ст₃. Поэтому, согласно рис. 1.6, а и формулам (1.12) — (1.14), получим

•w = -*=3- = ± )/(-^f^)* + Т*. (1.22)

Это максимальное (главное) касательное напряжение направлено под углом 45° к граням элемента, т. е. составляет с вертикалью угол у, равный 7=45°—а.

Из рассмотрения формул (1.19) и (1.20) следует, что o_y + a_x=Oi -+■ -f- or₃=const.

Таким образом, сумма нормальных напряжений на взаимно перпен­дикулярных площадках является величиной постоянной.

Очевидно, что при разноименной схеме (сжатие — растяжение) в формулах (1.19) — (1.22) напряжения о_х и а₃ надо брать со знаком ми­нус, т.е. знак перед <з_х и аз изменить на обратный.

Пример 1. На внешний элемент с горизонтальными и вертикальными гранями действуют напряжения (МПа): 0^=1300, с* = 700 и т=400 (одноименная схема сжа­тия). Определить о_и о₃ и т_тах.

Строим круг Мора (см. рис. 1.6,а). По данным значениям о*, о,, и т из точки С проводим окружность через точку В и находим: (Tj = 1500 и о₃=500 МПа; tg2a = =4/3 ; 2 a=53°10'; сс=26°35': т_тах=500 МПа.

Пример 2. Дано: сг»/ = 1 000, а_х=—500 и т=750 МПа (разноименная схема деформации). Определить at, сгз и т_тах-

Строим круг Мора (рис. 1.6, в). Из произвольной точки О в соответствующем масштабе откладываем: влево величину (отрицательная ось растяжения) а_х, вправо о_у. В крайних точках восстанавливаем перпендикуляры т=750 и соединяем точки В я В' прямой. Из центра С проводим окружность через точки В и В'. Отрезки OD и ОЕ будут характеризовать главные нормальные напряжения на наклонных площадках бес­конечно малого внутреннего элемента: o\ = OD= 1300, a₃ = 0£=800 МПа (растяже­ние). Угол наклона главных площадок 2а = 45°, а=22°30'. Точка F характеризует мак­симальное касательное напряжение в центральной точке внутреннего элемента Хт&_х= = СГ= 1050 МПа. Плоскость действия этого напряжения: у=45°—а=22°30'. Нор­мальное напряжение в этой точке характеризуется отрезком ОС; a_n=OC=250 МПа.

Аналогичные данные получим по формулам (1.19) — (1.22).

Объемное напряженное состояние

Внутри деформируемого объема тела при переходе от точки к точке на­пряженное состояние изменяется медленно, поэтому в окрестности лю­бой точки можно выделить бесконечно малый объем металла в виде па­раллелепипеда (рис. 1.7,а), в котором напряженное состояние можно

Рис. 1.7. Объемная схема напряженного состояния:

а —общий случай нормальных и касательных напряжений на площадках (гранях) эле­ментарного параллелепипеда; б — на площадках только глазные нормальные напряже­ния; в — напряжения на наклонной площадке треугольной призмы; г —круг Мора

рассматривать как однородное. Полное напряжение на каждой из шести площадок (граней) параллелепипеда можно разложить натри составля- ющие: одну по нормали к площадке—нормальное напряжение а и две в плоскости площадки — касательные напряжения т (на трех невиди­мых гранях напряжения а и т на рис. 1.7,а не показаны). Из курсов со­противление материалов и теория обработки металлов давлением изве­стно, что можно выбрать такую систему координат (осей х, у, z), в которой касательные напряжения на площадках равны нулю; такие пло­щадки называются главными, а нормальные напряжения на них — глав­ными напряжениями а_ь сг₂, а₃ (вместо а_х, о_у, a_z), причем в дальнейшем принимается, что ai>a2>cr₃ (рис. 1.7,6).

Однако, это не значит, что внутри объема выделенного параллелепи­педа (на гранях которого имеются только главные напряжения Оь сг, аз), нет касательных напряжений. Выделим в параллелепипеде наклон­ную площадку Л (на рис. 1.7,6 заштрихована), параллельную оси у и

2 2 2

Таким образом, можно определить напряжения ст_п и т, действующие на любой площадке, наклоненной под углом а.

Полученные выражения можно преобразовать следующим образом: перенесем полусумму главных напряжений в левую часть первого урав­нения; возведем в квадрат левую и правую части уравнений, исключив угол а, и получим

'• + (•».—2^)* ⁽¹'²³⁾

Это уравнение является уравнением окружности в координатах Оп—т, центр которой смещен по оси х=а_п на величину ((Т1 + сгз)/2 от начала координат, а радиус равен (<ji—стз)/2. Полученный круг назы­вается кругом Мора для определения напряженного состояния (a_n, т) на любой наклонной под углом а площадке, если известны главные на­пряжения ai и а₃ на главных площадках (рис. 1.7, в, г). Если а=0,то наклонная площадка совпадает с главной площадкой напряжения ai и

напряжению аг. Ha этой площадке в общем случае имеются нормальное а_п и касательное т напряжения (рис. 1.7,в). Рассмотрим условие равно­весия треугольной призмы, образованной сечением элементарного парал­лелепипеда наклонной площадкой. Проектируя все силы, действующие на призму, на оси, совпадающие с векторами а_п и т, получим: о_п dy (dz!cos а) = dy dz cos a + o₃dy dz tg a sin a;

т dy (dz/cos a) = a_x dy dz sin a — a₃ dy dz tg a cos a, или

<j_n = a_x cos² a + cr₃ sin² a; x = (a_x — a₃) sin a cos a;

cos 2a;

Рнс. 1.8. Круги Мора объемного напряженного состояния (а) и положение плоскостей максималь­ных касательных напряжений т«, и х₃₃ (б, в, г)

ai + or₃

a_x — cr₃

a! — ct₃

sin 2a.

т =

т=0 (точка В)\ если a=45°, sin2a=l и касательное напряжение яв­ляется максимальным (главным) и равным (точка С) т_Шах= (<Ji—сг₃) / /2=тз|.

Аналогичным образом можно построить круги Мора для наклонных площадок, параллельных осям х, z (т.е. векторам сг₃ и ai). Таким об­разом для объемного напряженного состояния всего может быть постро­ено три круга Мора. Очевидно, что соотношения между а_п и т определя­ются координатами точек, лежащих внутри большого круга (рис. 1.8, а, заштриховано).

Имеются три максимальных (главных) значения касательных напря­жений

Т31 = (^CTi — °з)/2; *₁₂ = К — сг₂)/2 ; т₂₃ = (а₂ — <т₃)/2,

действующих на шести взаимоперпендикуляриых площадках, располо­женных под углом 45° к осям (рис. 1.8,6, в, г), причем наибольшим яв- является тз1 (радиус большого круга); на этих площадках нормальные напряжения соответственно равны:

asi = (<?х + ог₃)/2; ст₂₁ = (а_х + а₂)/2 и а₃₂ = (а₂ + cr_s)/2.