5. Момент и мощность прокатки

Момент прокатки, прикладываемый к валкам со стороны их привода и необходимый для деформации (обжатия) металла (без учета потерь на трение в подшипниках валков), можно определить двумя способами: 1) по давлению металла на валки, зная плечо приложения равнодейст­вующей этого давления; 2) по расходу энергии при прокатке.

Первый способ рассмотрен выше и заключается в следующем. Для простого процесса прокатки и прокатки с натяжением полосы (при условии, что T₀~Ti) равнодействующая давления металла на валки на­правлена вертикально и момент прокатки (для ширины полосы b = 1), согласно формуле (II .29), равен

M_nv = 2 Ра = 2Рг|?/ = 2^/7_ср Р, (11.53)

где t{)=а/1 — коэффициент плеча приложения равнодействующей, оп­ределяемый по формулам (11.10) и (11.19); р_ср — среднее давление, оп­ределяемое по формулам (II.8, II.9) и (11.11, II.20) или по кривым рис.

2. 2, II.3; I — длина контакта, определяемая по формуле (1.59) для го­рячей прокатки и (1.62, II.14а) для холодной прокатки с учетом сплю­щивания валков.

При холодной прокатке с натяжением, когда заднее натяжение по­лосы не равно переднему (ТцфТ\), момент прокатки определяется по формулам (II.39) и (11.41).

Второй способ — определение момента прокатки по расходу энергии на деформацию (обжатия металла), заключается в следующем.

Как известно из курса механики, крутящий момент на валу (кН*м) можно выразить через передаваемую валом мощность N (кВт) или энергию А (квт-с) и угловую скорость о> (1/с) следующим образом:

М = N1 со - AIЫ = Alt-Rlv, (11.54)

здесь <ii — v/R,

где v — окружная скорость, м/с; R — радиус вала, м.

Рассмотрим применение этой формулы для двух случаев: при про­катке полосы прямоугольного сечения; при прокатке полосы фасонного сечения в калибрах.

1. Прокатка полосы прямоугольного сечения. Определим вначале ра­боту деформации при осадке заготовки высотой ho и шириной bо до ко­нечных размеров hi и Ь_х между параллельными плитами — штампами (см. рис. 1.13):

л.

dA = Pdh) А = J Pdh.

л#

Так как hi<h_Q, то для получения положительного значения работы деформации поменяем местами пределы интегрирования. Кроме того, примем, что в процессе деформирования р_сP=const, поэтому Р=р_сРЬ (при длине заготовки, равной единице, в направлении, перпендикуляр­ном показанному на рис, 1.13). При пластической деформации объем деформируемого металла остается постоянным V=h₀b₀=hib_l=hb = =sconst, поэтому b=V/h. На основании изложенного получим логариф­мическую формулу для работы деформации:

А = Pcv V [ dh/h = /7_СР V In (fig/h]), (И.55)

Ад

где Vln {h₀lhi) = V_CM — так называемый смещенный (логарифмичес­кий) объем металла.

Таким образом, работа (энергия) деформации про­порциональна среднему давлению и смещенному объему металла. Так как ln(fio/^i)^ 1, то очевидно, что смещен­ный объем может быть больше или меньше объема деформируемого металла (частицы которого при осадке изменяют свое положение непре­рывно). Так, при Ao/^i = l,5 получим: In 1,5 = 0,4 и Vc* ^в 0,4 К; при ho/hi—З получим In 3=1,1 и l/_CM=l,I V.

Процесс прокатки можно представить как процесс осадки металла между наклонными плитами — штампами (хордами АВ, см. рис. 11,1)’» поэтому формула осадки (11.55) будет справедлива и для случая про­катки.

Если прокатка осуществляется с кантовкой полосы, то общий рас­ход энергии при обжатии металла за несколько пропусков его через вал­ки следует определять по формуле

A =p_cpV In (h/L₀), (II.55а)

где L₀ и Li — длина полосы до и после прокатки.

Объем прокатываемого металла (при ширине полосы Ь = 1)

• = h₀ v₀1 — hi v₁1, (II .556)

где у₀ и У| — скорости входа металла в валки и выхода из валков; t— длительность прокатки.

Кроме того, согласно уравнению (1.70): v_x = v_B(\ +s), где s — опе­режение металла при прокатке.

Используя эти зависимости и уравнение (П.54), формулу (11.53) для момента прокатки представим в следующем виде (при b== 1):

M_av = p_cp\n(h₀lh₁)h₁R(l+s). (11.56)

С достаточной точностью можно принимать

In (Vfti) = In 1/(1 — г) & е/(1 — е/2) « 2е/(2 — е).

Таким образом, при прокатке полосы прямоугольного сечения без натяжения, или когда заднее натяжение равно переднему, момент про­катки можно определить по давлению металла на валки [см. формулу

53. ) или по расходу энергии [см. формулу (11.56)]. Достоинством фор­мулы (11.56) является то, что для определения момента прокатки не нужна величина плеча приложения равнодействующей. Однако опреде­

54. лить значение коэффициента плеча приложения равнодействующей для этого случая прокатки нетрудно при совместном решении уравнений

53. и (11.56):

1. (II.57)

   in (у/1_Х) hjR(l +s)

/^а

^=_т=

Для горячей прокатки, когда нет сплющивания валков, согласно уравнению (1.58), l² = RAh=Reh₀. Подставляя h_x=h_Q(\— е) и ln(/i₀//ii) = = е/(1—е/2), получим

1. 1 — е

(1 + S).

(II. 57 а)

2. 1—е/2

При обжатии г=0,15-г-0,3 и s=0,03-r-0,05 получим -ф=0,5-*-0,45, что соответствует указанным ранее значениям (см. с. 65).

При холодной прокатке полосы коэффициент плеча приложения рав­нодействующей следует определять по формуле (11.57). в которую надо

Рис. 11.26. К определению работы (энергии) де­формации металла при прокатке полосы с натя­жением

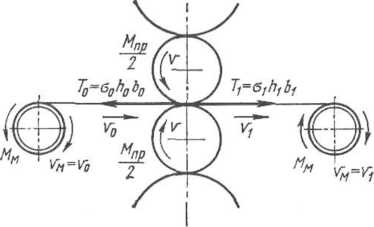
подставлять значение длины кон­такта с учетом упругого сплю­щивания валков.

Изложенные выводы спра­ведливы для простого процесса прокатки без натяжения и при холодной прокатке с натяжени­ем, но когда заднее натяжение равно переднему; в обоих этих случаях равнодействующая Р на­правлена вертикально (см. рис.

11. 18 и 11.23).

При холодной прокатке, ког­да заднее натяжение полосы не равно переднему, момент прокат­ки , прикладываемый к валкам, определим следующим образом (рис. 11.26). Очевидно, что общий рас­ход энергии на деформацию металла объемом V с толщины h₀ до тол­щины h_x (при ширине 6=const) не зависит от того, с натяжением или без натяжения осуществляется деформация. В данном случае работу деформации совершают валки, переднее и заднее натяжения:

А = А_в-{- А_{ — Л₀, (11.58)

где А_в — работа деформации, совершаемая валками.

Работа заднего натяжения Л₀ взята со знаком «минус», так как она уменьшает вытяжку (деформацию по длине) полосы.

Очевидно, что (при 6 = 1)

T₁ = a₁h₁; A₁ = T₁v₁t = T₁L₁ = T₁VJh₁ = o₁V;

Тq ⁼⁼ Oqhi, А₀ ~ T₀v_Qt = Т₀Lq = ТqVlh₀ = о₀V.

Согласно уравнению (11.58), работа деформации, совершаемая вал­ками

(11.59)

А_в = А — А_г-\- А₀, или, учитывая формулу (11.55)

Л_в = [р_с р In (M*i) — a_x + ст₀] V.

(11.60)

Согласно уравнениям (11.54) и (11.556) получим, что момент про­катки, прикладываемый к валкам при 6 = 1, равен (формула А. И. Це- ликова)

М_пр = [р_ср (M*i) — <?! + <т₀1 R (1 + s),

где Рср — среднее давление при прокатке без натяжения.

Очевидно, что заднее натяжение увеличивает, а переднее уменьшает момент прокатки на валках. Достоинством формулы (11.60), является

то, что для определения момента прокатки на валках не требуется знать точку приложения и угол наклона равнодействующей к вертикали [сравнить с формулой (11.38)]. Более точный анализ показывает, что пе­реднее и заднее натяжения уменьшают влияние контактных сил трения на общую работу деформации, поэтому момент прокатки будет несколь­ко меньше определяемого по формуле (11.60).

2. Прокатка полосы и фасонного профиля в калибрах. Момент про­катки определяют по практическим данным о расходе энергии. По рас­ходу энергии при прокатке блюмов, слябов, сортовых профилей и ли­стов на стенах различного типа и конструкции накоплено большое коли­чество практических данных, собранных на основе статистической обработки материалов о работе действующих станов. Эти данные могут

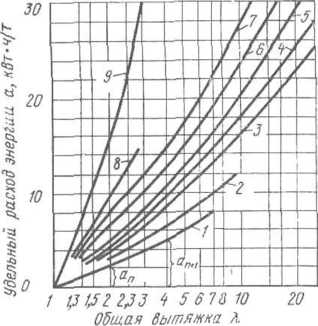
Рнс. 11.27. Кривые удельного расхода энергии главными электродвигателями при горячей прокат­ке низкоуглеродистой стали на различных станах:

1. — слябинге: 2 — блюминге; 3 — непрерывном проволочном стане 250 ; 4 — непрерывном средне­сортном стане 350; 5 — непрерывном заготовочном стане 700/500; 6 — рельсобалочном трехвалко­вом стане 800; 7 — крупносортном стане 500; 8 — автомат-стане трубопрокатного агрегата 250j 9 — прошивном стане агрегата 250

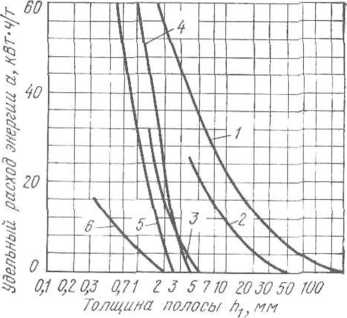
Рис. 11.28. Кривые удельного расхода энергии при горячей и холодной прокатке на полосовых станах:

/ — непрерывном широкополосном четырехклетевом стане 1700 горячей прокатки стальной поло­сы; 2 — двухвалковом стане 900 для прокатки цинка; 3 — реверсивном четырехвалковом стане 1700 для холодной прокатки дюралюминия; 4 — непрерывном четырехклетевом стане 1700 для холодной прокатки стальной полосы; 5 — непрерывном пятиклетевом четырехвалковом стане 1200 для холод­ной прокатки тонкой жести; б — стане для холодной прокатки меди

быть использованы при проектировании новых прокатных станов и выбо­ре типа и мощности двигателя для них, если проектируемые новые ста­ны по своей характеристике, конструкции и сортаменту проката мало отличаются от действующих.

Они особенно полезны для определения момента на валках при прокатке сортовых профилей в калибрах, так как в этом случае подсчет момента прокатки по давлению на валки затруднен сложностью определения контактной площади и среднего давления.

Практические кривые расхода энергии при прокатке обычно имеют вид, показанный на рис. 11.27 и 11.28.

По оси ординат откладывают удельный расход энергии а, выражен­ной в кВт-ч/т, т. е. работу, затраченную на прокатку 1 т данного метал­ла, а по оси абсцисс — вытяжку металла А, (по отношению к длине ис­ходного слитка или заготовки) или толщину листа и полосы. Так как зависимость расхода энергии от удлинения выражается некоторой сложной кривой, то для удобства эту зависимость строят по оси абсцисс в логарифмическом масштабе, что приближает кривую к прямой линии и делает использование ее более удобным.

81

Вследствие того, что начало кривой отнесено к длине исходной за­готовки (^=1), а возрастание расхода энергии — к увеличению общей вытяжки, очевидно, что расход энергии за данный пропуск металла че-

6. А. А. Королев

7. рез валки (при котором полученная ранее вытяжка увеличивается) оп­ределяется по кривой как разность двух ординат (см. рис. 11.27)

а = (а_п+1 — а_п), • (11.61)

где а_п+j и а_п — удельные расходы энергии при последующем и преды­дущем пропусках, кВт-ч/т.

Если массу прокатываемой заготовки (полосы и т. д.) обозначить через /я, то общий расход энергии за проход, кВт-ч

А = (д_п+1 — а_п) т. (11.62)

Расход энергии при прокатке измеряют но показаниям электричес­ких измерительных приборов, установленных в электромашинном зале прокатного цеха. В результате этого в полученные при измерении дан­ные входит и расход энергии на трение в подшипниках валков и пере­даточных механизмах главной линии стана в процессе прокатки. Одна­ко при построении кривых удельного расхода из полученных при изме­рении данных по расходу энергии исключается измеренная в то же время работа холостого хода стана, что делает эти кривые более точ­ными.

Если требуется ориентировочно определить по кривым расхода энер­гии, какова мощность, затрачиваемая на прокатку А/пр (кВт), и потери на трение в подшипниках валков N_w (кВт) при данном пропуске ме­талла через валки, при которых удельный расход энергии по кривой равен (Дти-1—^ап) (см. рис. II.27), то можно воспользоваться следующей формулой:

М_пр 4- р = [3600 (a_n+i ~ a_n)(t\ т, (11.63)

где t — длительность пропуска металла через валки, с.

При измерении расхода энергии во время холодной прокатки полосы с натяжением в общий расход энергии входит также и энергия, затра­чиваемая на создание заднего и переднего натяжений полосы, что необ­ходимо иметь ввиду при пользовании кривыми удельного расхода энер­гии (см. рис. 11.28).

Мощность электродвигателя для привода валков и крутящий момент на его валу состоят из трех частей

Л^дв - А/пр + ЛГ_ТР ± Л/дин = лг_ст ± ЛГ_ДИП; (11.64)

^дв = К_Р + К_Р ± Кш = Кг ± м;_ин, (н.б5)

где N_пр и М_Пр — соответственно мощность прокатки и момент прокат­ки, приведенный к валу двигателя, необходимые для совершения рабо­ты деформации (обжатия) металла валками; N_TP и Af_TP — соответст­венно мощность трения и приведенный к валу двигателя момент сил трения, возникающих в подшипниках валков (M_TPi ) и в передаточных механизмах (М_ТР2 ): шестеренной клети, редукторах, шпинделях и муф­тах; А/д_Ин и Мд„н — соответственно мощность и динамический момент, приведенный к валу двигателя, необходимые для преодоления инерции всех вращающихся от двигателя частей главной линии стана (валков, шпинделей, шестерен, муфт) в период разгона (плюс) или замедления (минус).

Первые две величины (N_np + N_TP) или (/И_пр+Мтр ) являются неиз­менными (постоянными по величине) в течение пропуска металла че­рез валки и называются статической нагрузкой двигателя.

Динамическая нагрузка двигателя (Л^_дин или М_днн) возникает толь­ко в станах со скоростью, регулируемой в течение процесса прокатки, или в станах с маховиком на валу редуктора в линии привода валков.

Рассмотрим, как определить отдельные составляющие нагрузки дви­гателя.

Момент прокатки, приведенный к валу двига­теля, легко определить зная: а) момент прокатки М_ПР, приложенный к валкам стана и необходимый для преодоления момента равнодейст­

вующих давления металла на валки относительно осей вращения; б) передаточное число редуктора i привода валков от электродвигателя, т. е.

= MJi. (11.66)

Момент прокатки определяют по усилию прокатки [см. формулы

29. , (11.41) и (11.46)] или по расходу работы (энергии), затрачивае­мой при прокатке [см. формулы (11.60) и (11.62)].

Момент трения, приведенный к валу двигателя, складывается из мо­мента трения в подшипниках валков и момента трения в передаточных механизмах:

М'т? ^{= =} AVI + M_rp2/i.

При прокатке металла на двухвалковом стане момент трения М_тр1> возникающий в четырех подшипниках двух валков, равен

Mtpi = ⁴ (^р/²) г_и = P[i_a d_a, (11.67)

где Р — полное усилие прокатки; ji_n — коэффициент трения в подшип­никах валков; d_n — диаметр шейки валка [для текстолитовых, открытых подшипников скольжения, см. рис. (III.9)], диаметр втулки подшипника жидкостного трения закрытого типа (см. рис. III.15) или средний диа­метр роликов для подшипников качения (см. рис. III.16).

При прокатке металла на четырехвалковом стане давление металла на рабочие валки передается на неприводные опорные валки, поэтому потери на трение возникают только в подшипниках опорных валков. Момент трения в этих подшипниках, приведенный к оси вращения при­водных рабочих валков, равен

M_rn = P\i_nd_a(D_p/D_on), (11.68)

где |Л_П, d_n — коэффициент трения и диаметр трения в подшипниках опорных валков; D_p и D_on — диаметры рабочих и опорных валков.

Для подшипников валков прокатных станов рекомендуется прини­мать следующие значения коэффициента трения |Л_П:

Для подшипников с коническими роликами 0,04

Для подшипников жидкостного трения 0,003

Для подшипников скольжения с металлическими (бронзовыми) вклады­шами < ... . 0,07—0,1

То же, с текстолитовыми вкладышами при скорости скольжения 3—1 м/с 0,01—0,02

Потери на трение в передаче от двигателя к валкам учитываем ко­эффициентом полезного действия (к. п. д.) передачи г]п. Тогда, не вы­числяя величины М_тр₂₎ сразу можно определить статическую нагрузку двигателя:

К, = (м„_Р + Чр.УЧ; = К, “«.• (Н-69)

Коэффициент полезного действия передачи можно представить как произведение к. п. д. шестеренной клети (14, = 0,92-4-0,95), редуктора (^2=0,95-^0,98 для каждой ступени) и шпинделей с муфтами (т\з1= = 0,99). Таким образом, получим г)_п='г]1'П2Т1з = 0,85-4-0,93.

Коэффициентом полезного действия прокатного стана называется отношение приведенного момента прокатки к приведенному статистиче­скому моменту:

■Пет = = —^se— _л = ! г, (11.70)

л<_т м_пр+м_тр1 1 + м_гп/м_п

В зависимости от конструкции подшипников валков момент трения составляет 6—12 % от момента прокатки, поэтому к. п. д. стана нахо­дится в пределах т)_ст = 0,750,85.

Динамический момент возникает только при изменении скорости прокатки в течение пропуска металла через валки (например, на ревер­сивных, толстолистовых и полосовых станах), а также на станах, в при­воде которых предусмотрен маховик (например, в трубопрокатных авто­мат-станах, листовых трехвалковых станах и т. д.).

При движении тела массой т с неравномерной скоростью v и уско­рением j динамическая сила равна Fj_a№—mj=m(dvlat). При неравно­мерном вращении тела предполагается, что его масса сосредоточена на окружности, радиус которой Ri называется радиусом инерции; при этом

v = (nR_if j = dv/dt = R_t (d(Dldt)_y

где dcafdt — угловое ускорение, 1/с².

Динамическая сила при вращательном движении равна

F_nm = mj = mRi (dco/dt).

Момент этой силы (динамический) относительно центра вращения M_WH=F_AimRi, или М_Аая - mRj (da/dt) = J (daldty.

Произведение mR\ называется моментом инерции вращающейся массы, a mD\ — маховым моментом.

Так как Ri=Di/2, то

= (da/di). (11.71)

Приведенный к валу двигателя маховой момент равен сумме махо­вых моментов масс всех деталей, вращающихся в линии стана:

mD] = mD\ + mD²_u + (mD² + тП²_ш + пЮ²_шп + mD²_B) 1 /i²,

где mD_n, mD_M, m£)_p, mD_m, mD_mn, mD_B — маховой момент соответствен­но якоря двигателя, моторной муфты с ведущей шестерней и маховиком на ней, ведомой шестерни редуктора, шестерен шестеренной клети и ко­ренной муфты, шпинделей и валков. Передаточное число i возведено в квадрат, так как живая сила массы пропорциональна квадрату частоты вращения, а последняя уменьшается по направлению от вала двигате­ля.

После определения М_ст и М_№н можно определять мощность главно­го электродвигателя. Двигатель выбирают в зависимости от того, для какого стана он служит приводом.

Станы с постоянной скоростью прокатки (нереверсивные)

Максимальную мощность двигателя этих станов определяют по мак­симальной статической нагрузке

^двтах ⁼ Л*ст ®дв> (11.72)

где содв — частота вращения якоря двигателя при данной нагрузке 1/с.

При длительном режиме работы электродвигателей допускается пе­регрузка & = 1,5-т-3,0, указываемая в каталогах. Поэтому номинальная мощность двигателя N_H=M_maJk.

Во многих случаях указываемая в каталогах номинальная частота вращения двигателя п_н, выбранного по мощности, превышает число оборотов в минуту валков п_в, определяемое технологически заданной скоростью прокатки v и диаметром валков D. Исходя из этого можно выявить необходимость в установке редуктора в линии привода стана с передаточным числом.

Станы с регулируемой скоростью прокатки (реверсивные)

Как было указано выше, на этих станах (блюмингах, слябингах, толстолистовых и т. д.) при прокатке металла возможно регулирование частоты вращения валков в течение каждого прохода: после захвата металла частота вращения валков увеличивается, затем прокатка про­исходит при постоянной (установившейся) частоте вращения валков и далее, перед окончанием прокатки частота вращения уменьшается. За­тем двигатель останавливается и реверсируется для пропуска металла в обратном направлении.

Прежде чем определить мощность двигателя, необходимо построить его нагрузочные диаграммы для всех профилей прокатывае­мого сортамента. Для примера на рис. II.29 приведена нагрузочная диа­грамма для одного пропуска металла через валки при реверсивной про­катке на блюминге, которая показывает, что изменение частоты враще­ния валков в течение каждого пропуска характеризуется трапецеидаль­ным графиком, изменение моментов двигателя — графиком в виде

Рнс. II.29. Нагрузочная диаграмма главного электродвигателя при прокатке на реверсивном блю­минге:

a — график изменения частоты вращения двигателя; б— статическая нагрузка двигателя; в — ди­намическая нагрузка двигателя; г — результирующая нагрузка за один проход металла через валки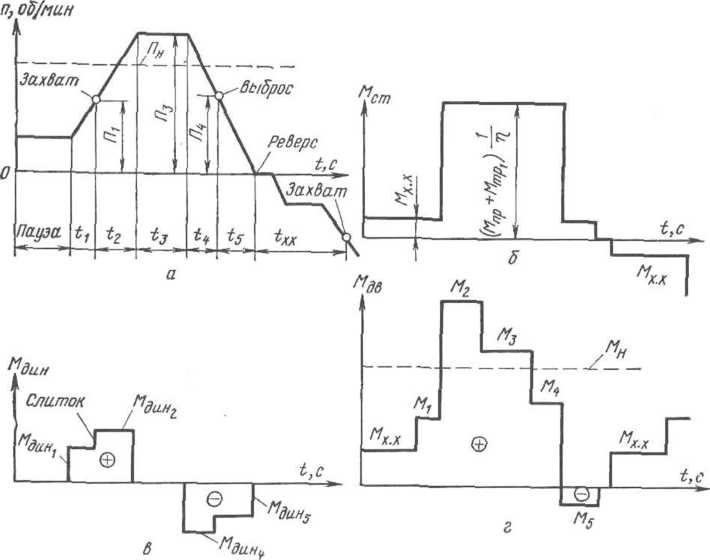

ступенчатых прямоугольников. Время прокатки включает периоды раз­гона, установившейся скорости и торможения. Обычно захват металла валками происходит в период разгона двигателя, а выброс его из вал­ков — в период торможения двигателя (чтобы уменьшить время, необ­ходимое для реверса).

В периоды разгона (ускорения) и торможения нагрузка двигателя складывается из статического и динамического (приведенных к валу двигателя) моментов:

1. При ускорении и торможении привода без металла в валках (без слитка)

Л*1 = м_ст1 + М_дт| = М_%% + 'UmD] (Ло/Д);

M_s = M_xs — 'ijnD] (da/dt), (11.73)

где М_х.I—момент холостого хода стана во время паузы между пропус­ками, который можно подсчитать, исходя из формулы

(11.74)

¹¹ 2(

Здесь mig — нагрузка на подшипник от массы одной вращающейся детали в линии привода (валков, шестерен и т. д.); ц*, ^ — коэффици­ент трения и диаметр трения в подшипниках данной детали. Обычно мо­мент холостого хода составляет 2—5 % от номинального момента двига­теля; mD ² — приведенный маховой момент массы всех вращающихся

деталей в линии привода; da/dt — угловое ускорение; обычно на блю­мингах принимают равным при ускорении 3,8-ь8,0 1/с² и при торможе­нии 4,0-ь 10,0 1/с².

2. При ускорении привода с металлом в валках

Щ = М„_г + М;_ш2» + _L _тщ JjL , (11.75)

где tnD] — приведенный маховой момент с учетом массы слитка (пола­гая, что масса слитка т находится на окружности валка диаметром D),

3. При торможении привода с металлом в валках

м, = м_ы- М_дйв4 = **9±*т . (11.76)

2. 2 где niDu =mDtt.

4. При прокатке с постоянной (установившейся) скоростью

= (M„_p + (И.77)

После построения нагрузочной диаграммы для всех пропусков ме­талла через валки приступают к определению номинального момента двигателя. Номинальный момент двигателя отпределяют из двух усло­вий: предотвращения нагрева двигателя при протекании большого тока в обмотке его якоря при больших нагрузках (моментах); допустимой кратковременной перегрузки двигателя, не вызывающей пробоя изоля­ции его обмотки.

Вследствие того, что ток в обмотке якоря двигателя пропорционален моменту, проверку по току заменяют проверкой по моменту,

1. Проверка на нагрев по моменту заключается в определении экви­валентного (среднеквадратичного) момента за весь период прокатки од­ного слитка (за все проходы металла через валки) по формуле

M_SK = У ^Mi V⁺ t ^ ⁺ -< М_т (11.78)

' (1+/₂ + (з + (.+ (ь = «ц

где £_ц— время цикла прокатки одного слитка.

2. Проверка на допустимую перегрузку:

^двшах^

где Ждвшах — максимальный момент двигателя по нагрузочной диаграм­ме; k — коэффициент перегрузки; для реверсивных двигателей постоян­ного тока £ — 2,5-ь2,75.

Таким образом, в обоих случаях номинальный момент двигателя дол­жен быть больше момента по нагреву и по перегрузке.

5. Примеры расчетов

Пример 3. Определить среднее давление металла на валки и полное усилие про­катки при горячей прокатке толстого широкого листа в четырехвалковон клети стана 2800.

Дано: диаметр рабочих валков стана £> = 800 мм; Л₀=40 мм; /гj = 30 мм; Л_ср =

=35 мм; Л/г =10 мм; е = 0,25; I— VRAh = 63 мм; ///г_ср = 1,8; u = 0,4; ib_n = 0,28; а=Д/г/г=0Д6 (9°10'). *