5. Прокатка на многовалковом стане

В четырехвалковом стане имеются два рабочих валка (меньшего диа­метра) и два опорных (большего диаметра). При прокатке давление металла на рабочие валки передается на бочки опорных валков и вос­принимается их подшипниками; таким образом, благодаря большой жесткости опорных валков (диаметр которых в 2,5—3 раза больше, чем у рабочих валков) прогиб их (и опирающихся на них рабочих валков) будет незначительным и профиль прокатываемой полосы будет иметь прямоугольное сечение (с весьма небольшой разнотолщннностью по ши­рине полосы).

Рассмотрим два случая: 1) приводными от электродвигателя явля­ются рабочие валки; 2) приводными являются опорные валки. В обоих случаях вращение неприводных валков осуществляется за счет сил тре­ния, возникающих в контакте между рабочими и опорными валками.

Примем следующее допущение: при качении опорных валков по ра­бочим (или наоборот) возникающие в контакте между ними силы тре­ния— качения весьма незначительны, и они не влияют на направление усилий, действующих на валки; таким образом, эти усилия не будут смещаться относительно геометрических точек контакта, лежащих на прямой, соединяющей центры валков.

1. Приводными являются р а б о ч и е в а л ки. Тогда, соглас­но рассмотренному выше, в общем случае внешние натяжения полосы могут быть не равны между собой {Т₀фТ\), поэтому равнодействующая Р (полное давление металла на рабочие валки) не будет направлена вертикально. Предположим, что Т₀>Т\ и равнодействующая Р направ­лена влево (в сторону большего натяжения), рис. II.22, а. При разло­жении Р получим, что горизонтальная сила Х=(Т₀—Т\)/2 изгибает рабочий валок в горизонтальной плоскости и воспринимается подшип­никами рабочего валка, а сила У передается на опорный валок. Если пренебречь потерями на трение в подшипниках опорного валка, то пол­ное давление на опорный валок равно P — Y.

Однако пренебрегать потерями на трение в опорных валках нельзя, так как их шейки характеризуются большим диаметром d_Qп, и при боль­ших значениях усилия У момент трения будет значительным. Что каса­ется потерь на трение в подшипниках рабочих валков, то их можно не учитывать, так как сила X незначительна и диаметр цапфы рабочего валка невелик.

Таким образом, если учесть потери на трение в опорных валках, то усилие Роп будет направлено по касательной к кругу трения, радиус трения которого роп=Цоп^оп/2. Здесь ц₀п — коэффициент трения в под­шипниках опорных валков (см. рис. II.22,6).

Рис. 11.22. Направление усилий на рабочие н опорные валки четырехвалкового стана:

а —при прокатке с натяжением (Го>Г|); б —с учетом трения в подшипниках опорных валков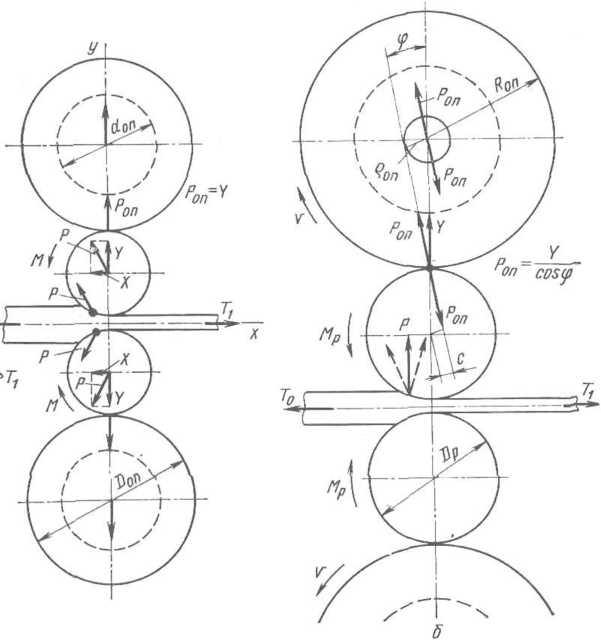

Это направление силы Р не зависит от того, какое направление име­ет полное давление металла Р на рабочие валки: вертикальное или на­клонное (указано штриховыми линиями), т. е. не зависит от величины натяжений Т₀ и 7V Однако величина силы Р_оп зависит от натяжения Т₀ и Г, и направления равнодействующей Р. Очевидно, что

Рon Wcoscp, sin ф = p_on/R_on — И'оп ^оц/^оп* (11.43)

где ввиду незначительного отклонения равнодействующей Р от вертика­ли (согласно рис. 11.22) можно принимать У ж Р.

Момент трения в подшипниках опорных валков

М_Тр.₀П = 2Род Роп ~ ^И'ОП^ОП* (11.44)

Для того, чтобы вращать опорные валки и преодолевать этот момент трения, к двум рабочим валкам со стороны их привода потребуется при­ложить дополнительный крутящий момент, равный

•^ТР.ОП ⁼ ^оп (^р/^оп)* (11.45)

Таким образом, общий момент, который потребуется приложить к рабочим валкам, равен

Л1р = А/др -}- Af_Tp ₀п> (11.46)

где М_Пр — момент, требующийся для деформации металла (момент про­катки), определяемый по формулам (11.39) и (11.41).

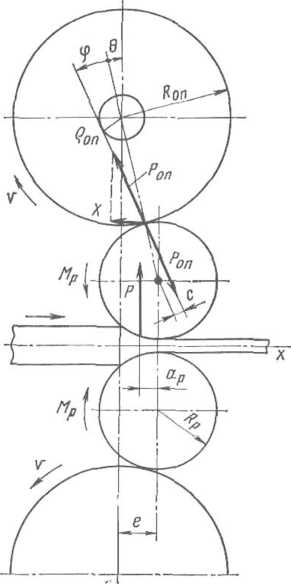
На станах с постоянным направлением прокатки листов и полосы (нереверсивных) часто устанавливают подушки с подшипниками рабо­чих валков таким образом, чтобы рабочие валки были смещены (на 5—

10. мм) относительно опорных валков в направлении движения метал­ла (на рис. 11.23 вправо). Практика показывает, что при этом достига-

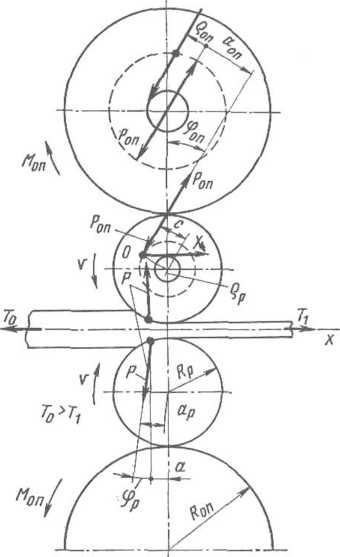
Рнс. 11.23. Направление усилий на рабочие и Рис. 11.24. Направление усилий на рабочие и опорные валки в случае смещения рабочих опорные валки с учетом трения в подшипни- валков по отношению к опорным ках в случае привода опорных валков

ется большая устойчивость положения рабочих валков, т. е. более пра­вильное соприкосновение рабочих и опорных валков по образующим их цилиндрических поверхностей (обеспечивается большая точность па­раллельности образующих в плоскости, проходящей через центры опор­ных валков). В этом случае угол смещения составит sin0 = е/(/?_р+/?_Оп), а угол наклона силы Р_0п к вертикали увеличится и будет равен ср+0. Если принять, что равнодействующая Р направлена вертикально, то из условия равновесия рабочего валка получим

Р - Р_ш cos (Ф + в) = 0; Р_ш = Р -1— , (11.47)

COS (Ф -f- 0)

т. е. сила Р_0п будет несколько больше, чем в случае, когда смещения нет [см. формулу (11.43)]. Однако ввиду небольшой величины углов ср и 0 в данном случае момент трения опорных валков, приведенный к оси вра­щения рабочих валков, можно подсчитывать по формуле (11.45).

2. Приводными являются опорные валки (рис. 11.24). Такую схему привода применяют, когда при малом диаметре рабочих валков (и еще меньшем диаметре их шеек) передавать большие крутя­щие моменты, необходимые для прокатки металла, рабочими валками практически невозможно ввиду чрезмерных напряжений на кручение, возникающих в шейках валков со стороны их привода.

Рассмотрим сначала условие равновесия неприводного рабочего валка. Положим, что То>Т_х. При направлении сил Р и Роп влево в под­шипниках рабочего валка возникает горизонтальная сила X, касатель­

ная к кругу трения радиусом р_р. Проектируя все силы (пересекающиеся в одной точке О) на горизонталь, получим

• Р sin <рр — Р_оп sin фоп + X = О, откуда

X = Р sin ф₀ + Р₀п sin Фоп* (И-⁴⁸)

Составим также условие равновесия моментов сил, приложенных к рабочему валку: Pa_p-f-Xp_p— Р_опс = 0.

Подставляя сюда значение X по формуле (11.48), получаем выраже­ние для определения угла наклона силы Р_оп (при c=R_p 8Щф₀п):

sin ф_оп = Р/Р_оп [(а_р + р sin <р_р)/(Я_р + Рр)1. (И.49)

Ввиду небольшой величины второго члена в числителе можно при­нимать

sin ф_оп = М_пр/[Р_оп (Я_р + р_р)1, (II.49а)

где Мщ₎=Ра_1> — момент прокатки, определяемый по формулам (II.38) и (11.41).

Определим момент, который необходимо приложить для вращения одного опорного валка:

М₀ц — Роп (^аоп 4" Роп)» (11.50)

ГДе Ооп ⁼ ^оп sin фот Роп⁼⁼М^,оп С?оп/2.

Рис. 11.25. Направление усилий на валки в многовалковом (12-валковом) стане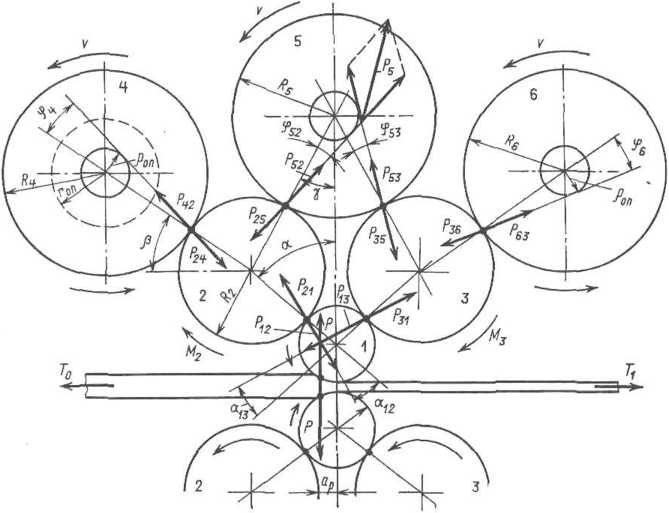

Подставляя значение sin фон по формуле (II.49а) и пренебрегая по­терей на трение в подшипниках опорного и рабочего валков (роп=р_Р= =0), получим

М_оп = М_пр(Я_оп/Я_р). (11.51)

Таким образом, для осуществления деформации металла (прокат­ки) в случае привода опорных валков к ним потребуется приложить мо­мент в Ron/Rt>=2-t-2£ раза больший, чем при приводе рабочих валков; это обстоятельство надо учитывать при проектировании четырехвалко­вого стана с приводными опорными валками.

Рассмотрим схему действия сил при прокатке на 12-валковом стане (рис. II. 25). Приводными являются валки среднего ряда, т. е. валки 2 и 3.

Определим сначала направление сил, действующих на основные опорные валки (ролики) 4—6. Очевидно, что эти силы направлены по касательным к кругам трения, радиус трения которых р₀п=р.ол^оп/2, Т. е. Sin ф₄ = роп/^4; Sin ф52 = роп/-^5 и т. д.

Затем составим условия равновесия рабочего валка 1; примем, что T₀=Ti и сила Р направлена вертикально вверх:

а) Ра_р—P[₂^isin ai₂—Pi₃Pisin ai₃=0; sin cci₂ = sin ai3=-Po_p/[(Pi2-(-Pi3)i?₁];

б) P—^i2COs(a—CC12)—Pi₃cos(a-fan) =0;

в) /^>i2Sin(a—ai₂)—-Pi3sin(a+ai₃) =0;

P\2 = P/[cos(a—a₁₂)-}-sin(a—a,₃)]; Pi3=P/[cos(a+aj3)-f sin(a-f-a₎₃)].

Далее составим уравнение равновесия приводного промежуточного валка 2 (или валка 3, что одно и то же ввиду симметричности схемы расположения валков):

а) P24COs(p+<p₄)— P₂5COs(y—ф₅₂)— P₂isin(a—ai₂) =0;

б) — Р₂45т(р + ф₄) +P₂5Sin(v—Ф52) +P₂iCOs(a—a_}2) =0.

Так как Ръх^Рп известно, то из этих двух уравнений можно опреде­лить неизвестные Р₂₄ и P₂s;

в) M2—P24R2 sin ф₄—Р₂5^2 sin ф52~ Р2\R.2 sin ai₂ = 0;

М2— V₂P«p {Rl/Ri) + (P24+ P25) (~~) Роп-

f?4

Таким образом, момент, необходимый для привода двух промежу­точных валков:

М₂ + М₃ = М_пр {RJR&2 + (Р₂₄ + Р₂₅)(Р₂/#₄) Роп, (Н.52)

где М_пр=2Ра.р — момент прокатки [см. формулы (II.29), (11.38) и (11.41)]; Р — полное давление металла на рабочие валки при прокатке, определяемое с учетом упругого сплющивания валков.