5. Влияние внешних зон

при горячей прокатке толстой полосы

Выше было указано, что формулы (П.8), \Н.9), (И.И) и (U.20) идеаль­ного и реального процессов прокатки справедливы только для случаев прокатки без натяжения широкой полосы, когда ///*<•,;> 1, т. е. когда схе­ма деформации металла в валках является двухмерной (плоской) и уширением можно пренебречь.

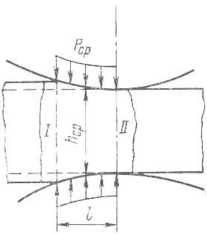
При горячей прокатке весьма толстой полосы (слитков, блюмов, сля­бов и заготовок) с небольшими обжатиями, когда в первых пропусках высота сечения металла больше длины контакта (Л,_РД>1), коэффици­ент контактного трепня оказывает небольшое влияние па среднее давле­ние (р.^ 0,4^-0,5), в этом случае преимущественное влияние оказывают так называемые внешние зоны I и II деформируемого металла, распо­ложенные слева и справа от геометрической зоны деформации I (рис. 11.11, а, б) п испытывающие внеконтактиые напряжения и деформации.

При прокатке весьма толстой полосы, когда /*,.,,//> 1 (т.е. 1//г_С\з<.1), среднее контактное давление с уменьшением l/h,_p не уменьшается (как рассмотрено выше для случаев прокатки при l/h_cv>-l), а увели­чивается. Качественное изменение (минимум) кривой Pc_P/k=f(l/h_cр) находится в интервале значений //Л_{р = 0,6ч-1,0 (рис. 11.11, в).

На основании экспериментальных данных А. И. Целиков и В. В. Смир­нов предложили учитывать влияние внешних зон в области /i_cp//;> 1

(//Лср<1) КОЭффшШСНТОМ //в.rj.

С учетом последующих экспериментальных данных для случая про­катки относительно толстой полосы величину коэффициента влияния внешних зон можно представить формулой

4

^В.З — } hcpf I • (11,26)

Рср/к

I и

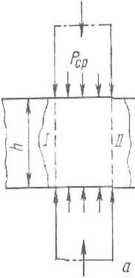
Рис. 11.11. Влияние внешних зон при деформации тонкой полосы при l/h_c_ <1 (т. е. *ср^-^>^^:

а — осадка металла: 6 — прокатка; в — кривые увеличения среднего давления (отно­шения р _Gp//d) при //ft _с„ - I

Таким образом, согласно формуле (11.21), при горячей прокатке весь­ма толстой полосы, когда l/h_cpCl и |x = 0,4-f-0,5, среднее контактное давление можно определять по формуле

T ⁼ (^,+ii)ⁿ->^{: (П}-^21а)

соответствующая кривая показана в левой части на рис. II.2, где об­ласть влияния внешних зон при l/h_cР<С1 обозначена Б.З.

Для определения давления с учетом влияния внешних зон А, Д. Том- леновым предложена теоретическая формула

pjk = 0,5 l/h_cv + hjl (0,6 — 0,04/г_ср//). (11.216)

Расчеты по этой формуле дают результаты, близкие к эксперимен­тальным данным (при (.1 = 0,5).

5. Давление на валки при прокатке сортовых профилей

При горячей прокатке сортовых профилей (круга, квадрата, рельсов, балок, швеллеров и др.) возникают дополнительные силы трения на бо­ковых стенках калибров, которые увеличивают давление па валки и мо­мент прокатки. Однако точно учесть влияние этих дополнительных сил трения, а также неравномерности деформации металла в калибрах с по­мощью теоретических формул не представляется возможным; удовлет­ворительные решения имеются только для случаев прокатки в простых открытых калибрах (квадратных, ромбических, овальных). При опреде­лении давления па валки для случаев прокатки сложных фланцевых про­филей (рельсов, балок) более надежным является метод, основанный на использовании экспериментальных данных.

В соответствии с этим методом давление па валки можно представить в функции так называемого коэффициента напряженного состояния ме­талла при прокатке в калибрах (или коэффициента формы калибра):

pjk ■ л„; и„ - я (у- + b -0&) > 1, (И .27)

• Лер I

где а и b — коэффициенты, зависящие от формы калибров; /г_ср— сред­няя приведенная толщина полосы в зоне деформации; I — длина контак­та металла с валком (горизонтальная проекция дуги захвата).

Для случаев прокатки, когда 1<//Л_Ср<2, можно рекомендовать сле­дующие значения коэффициентов а и Ь:

1. а = 0,5 и Ь = \ —прокатка простых профилей (узкая полоса, плос­кий овал), когда схема деформации приблизительно соответствует плос­кой (двухмерной);

2. а = 0,6 и 6 = 0,8—для овальных и круглых калибров;

3. а = 0,7 и Ь — 0,5 — для квадратных и ромбических калибров;

4. а = Ь=0,8 — для фасонных закрытых калибров;

эти значения коэффициентов можно применять во всех случаях, ког­да объемная схема деформации значительно отличается от плоской схе­мы деформации (т. е. когда имеется свободное или стесненное ушире- ние).

Для случаев прокатки, когда //А_ср>2, можно считать, что схема де­формации металла в калибрах является плоской (приближается к слу­чаю прокатки относительно широкой полосы) и коэффициент напряжен­ного состояния (формы калибров) равен

п_к = 0,75 + 0,25l/h_cv. (II.27а)

При прокатке металла в калибрах условную толщину полосы (заго­товки, профиля) определяют, исходя из начального F₀ и конечного F\ поперечных сечений полосы в данном проходе, т. е.

h₀ ~ FJb$\ hi — F-Jby\ Ah — Hq h

Л_ср --= (A. + К)!2\ b_cv = {b₀ -h b_x)/2.

Длина контакта определяется по формуле /«]/ RAh, где R — радиус валка в данном калибре.

Общее (полное) давление металла на валок (усилие на валки при прокатке)

р = Рс р /Ь_ср = Рс V (11.276)

Рис. 11.12. Графическое определение площади горизонтальной проекции поверхности сопри­косновения металла с нижним валком при прокатке ромбической полосы в квадратном ка­либре. Цифры показывают последовательность построения

где F_y<—контактная площадь (горизонтальная проекция поверхности соприкосновения металла с валком).

В случае затруднений при определении / и Ь_ср (например, при про­катке сложных профилей) при пользовании формулой (11.276) контакт­ную площадь F_l{ рекомендуется определять графическим способом. Для этого калибр с металлом по правилам начертательной геометрии вычер­

чивают на миллиметровой бумаге в трех проекциях и по линии пересе­чения соответствующих точек валка и металла определяют контур го­ризонтальной поверхности контакта металла с валком (рис. 11.12).

Момент прокатки определяют по формуле (для двух валков)

M_nv = 2Pa_K = 2P%l, (И.27в)

где Tj)_K=^aK// — коэффициент плеча а_к приложения равнодействующей Р (усилия на валки) при прокатке в калибре.

Для случаев прокатки простых профилей (узкая полоса, плоский овал) i|),_{ = 0,45-7-0,5.

Для случаев прокатки более сложных и фасонных профилей ввиду значительного влияния дополнительных сил трения в калибрах коэффи­циент имеет повышенные значения. Можно принимать: при прокатке в круглых и ромбических калибрах i|)_K=0,6-f-0,65; при прокатке в за­крытых (фланцевых) калибрах iJjk = 0,65-^0,75.