4. Влияние упругого сплющивания валков при холодной прокатке

При определении длины контакта с учетом упругого сплющивания вал­ков по формулам (1.62), (1.63) и (1.64) надо знать фактическое сред­нее давление металла на валок при прокатке с натяжением или без на­тяжения, определенное также с учетом влияния сплющивания валка, которое вызывает увеличение параметра ///г_ср.

Так как при упругом сплющивании валка длина контакта увеличи­вается и становится равной /_с (см. рис. 1.29), то при определении сред­него давления по формулам (II.8), (11.9), (11.11) или (11.23) вместо па­раметра m = [ilfhcp надо принимать параметр w_c=jjic//icp, причем т_(;> >т\ /_с>/.

Таким образом, для определения фактической длины контакта /_с или параметра т₍- с учетом упругого сплющивания валка имеем систе­му двух уравнений (для общего случая прокатки полосы с натяжением):

1. уравнение (11.23), которое представим в следующем виде [ с уче­том формулы (11.8) ] :

Pcp!(k_Cvⁿo) = 1 !т_с(е^Пс— 1);

илн

(II.23а)

2. уравнение (1.62), которое представим в следующем виде, подста­вив вместо Х\ его значение из формулы (1.63) при р_Ср=р"р :

1_С — х_г V RAh + xi 1 I' -I- xi ; I' - 2xi l_z =-- i²;

или, разделив левую и правую части па kc_Pn_a ,

Приравнивая правые части этих уравнении, получим (формула ав­тора)

(11.24)

ml - nf -f b_c(e^m° — 1),

где коэффициент b_c = C(k_cv—<у_ср) Оц.//г_ср.

Из рассмотрения уравнения (II.24) следует, что неизвестная вели­чина— параметр т,- входит в левую и правую его части, поэтому непо­средственно решить это уравнение нельзя.

Решение возможно тремя методами.

1. Методом последовательного приближения — подбором значения т_с до совпадения значении левой и правой частей уравнения при задан­ных значениях т и коэффициента Ь_с.

Например, дано: /72 = 1; Ь_с~ 0,3;

а) задаемся т₍ ==1,2 н находим

1,44= 1 +0,3(3,32—1) = 1,696 (несовпадение);

б) задаемся пи =1.4 и находим

1,96= I -[-0,3 (4,055— 1) = 1,916.

Получили так называемую «вилку»: в первом случае правая часть больше, а во втором меньше левых частей;

в) задаемся ш< = 1,38: получим точное совпадение.

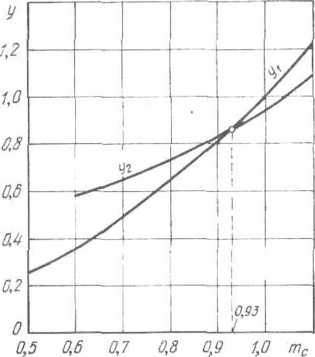
2. Графическим методом; в этом случае уравнение (11.24) предста­вим в следующем виде:

tji = ml) у2 = m" + b_c (е’^с — 1 ).

Строим две кривые: tj\=f(tn_c) и ^=/(^г_с); пересечение кривых да­ет точное значение т_с. Например, для значений т = 0,5 и 0_С = 0,4 пере­

сечение кривых дает значение т_с = 0,93 (рис. II.8). Если кривые не пе- ресекаюгся, то надо изменить исходные параметры прокатки т и Ь_с.

3. Точным решением уравнения (11.24), которое представим в еле' дующем виде

b_c = (ml — m²)/ (e^ml — l). (II.24a)

а также в виде, удобном для программирования и расчетов на ЭВМ b_c = (mi — т²)/(ехрт_с— 1), где ехр т_с = е^тс.

На рис. II.9 представлены кривые m_c=f(b_c), построенные, по дан­ным расчета на ЭВМ (для различных значений т~const). Параметр т

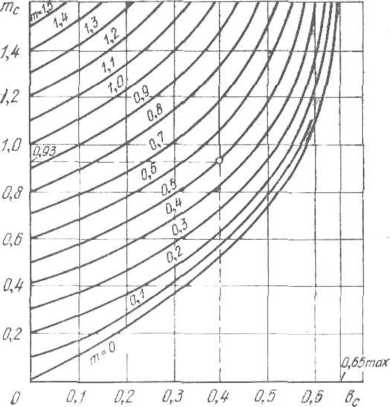
Рнс. II.8. Графическое определение коэффици- Рис. П.9. Номограмма для определения т_с ента т _{с по} заданным значениям т и Ь_с

имеет небольшую величину (т<0,5), поэтому яг_с<1; в этих случаях можно принять, что е^тс= l+m_c+mi/2+mc /6+...« l-f-m_c-|-0,6 ml и с достаточной точностью определить значение параметра согласно форму­ле (1.24) по приближенному выражению

1 ~0,6Ь,; ^Ь1

т_г =

2(1 — 0,6 ь_с)

1 + у 1 + (2 тУ

Практикой установлено, что при холодной прокатке тонкой стальной полосы может наступить такой момент, когда дальнейшее ее обжатие становится невозможным ввиду того, что упругое радиальное сжатие (сплющивание) валков оказывается равным толщине полосы (см. рис.

1.29).

Определим минимальную (предельную) толщину полосы, при кото­рой наступает предел возможности ее пластической деформации в вал­ках, т. е. обжатие Ml — 0 и в = 0. В этом случае / = К/?А/г=0; т = =¹|а(^/Лср)=0; /i₀=/i_cp=/i 1 = fimin, и согласно формуле (II.24) коэффи­циент Ь_с будет равен

Ь_с = С (k_cf> — сг_Ср) (11.246)

Функция (II.24а) имеет максимум (при т — 0), когда (2—т_с) — —2 = 0; это трансцендентное уравнение имеет единственное решение при т_с=1,б (точнее 1,594), при котором fr_Cmax = 0,65 (точнее 0,048), поэтому из уравнения (II.246) получим (формула автора) h_mm, мм:

^min 1,54С (&_ср— о_ср) D\i, (11,25)

где D = 2R — диаметр рабочих валков; fc_Cp = l,15 [(<J_To+a_Ti)/2]—сред­нее сопротивление деформации материала полосы; о_ср~ (cro-f-cri)/2— среднее натяжение полосы при прокатке; а_т0 и o_Ti — предел текучести материала полосы до и после прокатки; о₀ и ся —заднее и переднее на­тяжения полосы.

При достижении «предела прокатываемости» полосы h_min при т_с = = 1,6 согласно формуле (II.23а) получим предельное (максимальное) значение отношения Рср/(&ср—а_Ср) =2,5 (точнее 2,46), при котором, со­гласно формуле (1.61),

q/lR(k_cp — o_cvy\ = \00k_y = 12,5С = const;

здесь следует отметить, что р_сР и q не зависят от коэффициента трения р.

Таким образом, получение при холодной прокатке минимальной тол­щины полосы /Zmin [формула (11.25)] возможно при различных значени­ях q и (fc_Cp—а_Ср), но отношение q к квадрату (k_cp—ог_ср)² для данного ра­диуса (диаметра) валков должно быть строго определенным и постоян­ным. При правильном применении этого отношения минимальную толщину полосы (мм) можно определять по более простои формуле

ftmin = 0,25\iq/(k_cv — <j_cp), (II.25а)

в которой влияние радиуса валков учитывается величиной q, определен­ной по предыдущей формуле.

Если валки изготовлены из легированной стали, для которой С = = 1,08-10^-5 мм²/Н (см. с. 33), то получим h_m|_П, мм:

^min = о, 166 (k_cp — о_с р) D\l • Ю^-4 = 0,25 \iq/(k_cp — а_ср), (И.256)

где

q = 66 (k_cp — ст_ср)* D • 10^-6;

здесь k_cP и стар — в МПа; q — в Н/мм; D — в мм.

Для обеспечения возможности получения при прокатке минимальной толщины полосы необходимо:

а) увеличить натяжение полосы (переднее и заднее, см. формулу

11. 25 б);

б) уменьшить диаметр валков;

в) уменьшить нагрузку q по ширине полосы;

г) уменьшить коэффициент контактного трения, т. е. улучшать каче­ство технологической смазки поверхности валков и полосы.

Формула (11.25) и выводы из ее анализа позволяют дать теоретиче­ское обоснование создания и применения так называемых многовалко­вых станов (12- и 20-валковых). Конструкция этих станов (см. рис.

2. 1.7) позволяет применять рабочие валки минимального диаметра (6—30 мм), которые можно изготовить из твердого сплава, например, карбида вольфрама, для которого модуль упругости Е в три раза выше, а константа упругости k_Y и коэффициент упругости С валков в три ра­за ниже, чем для стальных валков. В этом случае согласно формулам

25. при С = 0,36-10~⁵ мм²/Н получим h_m\n, мм:

А_Ш1л - 0,055 (4_СР — а_ср) Оц • 10 *. (П.25в)

Рассмотрим теперь вопрос о влиянии упругого сплющивания валков на момент прокатки, необходимый для пластической деформации ме­талла в валках.

Вследствие упругого сплющивания валков сечение выхода металла из валков, проходящее через точку В, сместится вправо и пройдет через точку В' (рис. 11.10). За счет упругого сплющивания валко в (увеличе­ния l/h_Ср до k/hcp) площадь эпюры давлении р_х увеличилась как слева, так и справа от геометрической оси валков, проходящей через точку В; моменты этих дополнительных площадей относительно оси валков рав­ны между собой и обратны по знаку. Таким образом, работа, затрачи­ваемая на пластическую деформацию полосы, не зависит от того, есть упругое сплющивание или нет, что соответствует известному положению

о том, что упругая деформация является обратимой. В данном случае энергия упругой деформации валка (упругого радиального сжатия) при возрастании давлений р_хс (левая часть эпюры — зона отставания метал­ла при прокатке) восстанавливается при уменьшении давлений р_хс (пра­вая часть эпюры — зона опережения металла при прокатке).

Из изложенного следует, что

Mi = Ра - Р_са_с’, ci_c!ci Р/Р_с — (pjp_cv._c) Шс>

где а_с и а — значения плеч приложения равнодействующих с учетом и без учета упругого сплющивания валков.

Согласно уравнениям (II.8) и (11.23а) получим

_aJa = (е^т— 1 ) (е”^с — \) &т{\ -|- m/2)/[m_c(l + mJ2)\. (П.25г)

Puc. U.IQ. Положений р а в на ист ау и ш.и х Р я Р _с давления на ва.чки без учета И с учетом упругого сплющивания валка

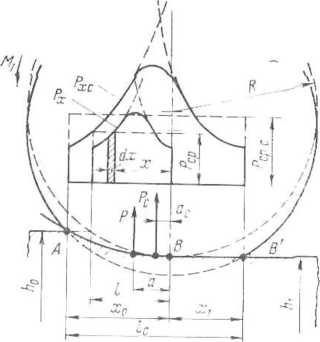
Например, для рассмотренного выше случая (см. рис. II.8) /гг = 0,5, Ь_с = 0,4 и т_с = 0,93 получим а_с/а = 0,425.

Таким образом, при холодной про­катке полосы (листа) можно прини­мать, что отношение коэффициентов плеч приложения равнодействующих \|.i_c/ij)=0,4 ч-0,7.

Согласно формуле (П. 14а) коэф­фициент плеча приложения равнодей­ствующей без учета упругого сплю­щивания валков (при горячей про­катке) ^ = 0,45-ь0,5, поэтому при хо­лодной прокатке с учетом влияния уп­ругого сплющивания валков коэффи­циент плеча приложения равнодейст­вующей будет равен: \\\ = а,/1 = 0,2-^- -0,35.

Полное усилие на валки при про­катке полосы шириной b [см. (11.11)].

Рс ⁼ Рср-с

где Рср.с — согласно формуле (II.23a), l₍. = rn_ch₍pl|li; т_с — согласно фор­муле (11.24) или по кривым, приведенным на рис. II.9. Момент прокатки

М_пр 2М_Х = 2Р_с а_с = 2Р_С ^ I (0,4 - 0,7) Р, I. (11.25д)