3. Влияние натяжения полосы при холодной прокатке

При холодной прокатке тонкой полосы применяют натяжение при вхо­де полосы в валки (заднее натяжение) и при выходе ее из валков (пе­реднее натяжение). Практикой установлено, что без значительного натя­жения нельзя прокатать тонкую полосу и получить равномерную толщи­ну ее по ширине и длине. Применение натяжения, кроме того, позволяет значительно уменьшить давление на валки при прокатке и способствует получению хорошего качества поверхности полосы.

Натяжение применяют и при горячей прокатке тонкой полосы, напри­мер, на непрерывных полосовых станах (натяжение между клетями ста­на с целью устранения образующейся петли), однако это натяжение не­значительно и обычно в расчетах его не учитывают.

Холодную прокатку топкой полосы осуществляют с применением смазки, подаваемой на валки и на полосу со стороны входа ее в валки, поэтому коэффициент контактного трения имеет небольшую величину (в зависимости от качества смазки ju = 0,044-0,1). Согласно приведенному выше анализу, при холодной прокатке тонкой полосы по всей длине кон­тактной поверхности при этих значениях коэффициента трения наблюда­ется скольжение металла относительно валков и эпюра нормальных дав­лений имеет пикообразную форму (см. рис. II.1), соответствующую иде­альному процессу прокатки.

Ввиду небольшой величины контактных сил трения можно считать, что вертикальные (р_Л\~ o_v) и горизонтальные нормальные напряжения в объеме деформируемого металла являются главными нормальными

напряжениями оi и а₃, и поэтому для всей зоны деформации справедливо уравнение пластичности (II.3) в главных напряжениях:

р_х — о_х = k\ p_x = k + а_х.

При прокатке без натяжения эпюра внутренних напряжений сжатия Ох, возникающих под действием контактных сил трения, согласно урав­нению пластичности, подобна эпюре р_х, но ординаты ее меньше на ве­личину k (рис. II.7, я), т. е.

^х Рх (II.За)

При прокатке с натяжением к полосе прикладываются внешние рас­тягивающие напряжения: во входном сечении А — заднее удельное на-

Рис. II.7. Эпюры распределения р_х и а_х по длине контакта при прокатке: а—без натяжения полосы; б— с натяжением полосы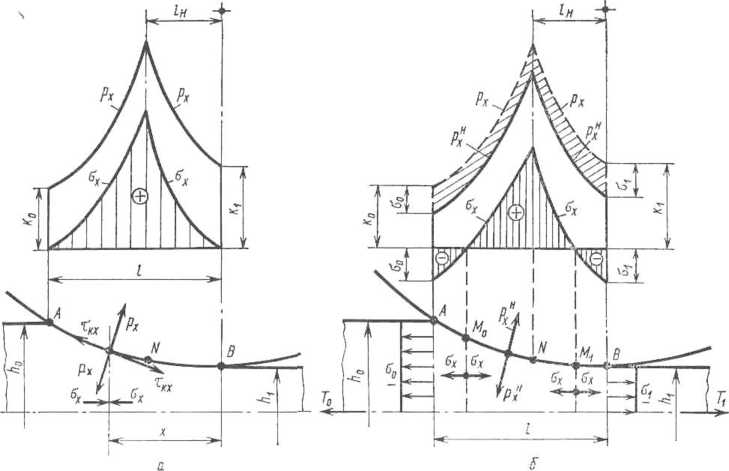

тяжение о₀; в выходном сечении В — переднее удельное натяжение ац эти натяжения (растяжение) уменьшают внутренние напряжения сжатия в металле а_х вследствие уменьшения влияния подпирающих контактных сил трения (рис. II.7, б).

При прокатке без внешних натяжений во входном А и выходном В сечениях, очевидно, горизонтальные напряжения в металле равны нулю (о._х~ол = (Ув = 0), что и было принято во внимание при выводе уравне­ний (II.5) и (II.6) для идеального процесса прокатки.

При прокатке с приложением внешних растягивающих напряжений (принятых отрицательными) в сечениях А и В уравнение пластичности (II.3) имеет знак «плюс» в левой части, так как здесь сг_х = лгд = —сг₀ и <7л =Оц — —<7|, Т. е.

р_л = (— о₀)=р_А + о₀ = 6; P₃-(-°_l) = p_B-t-<J,"=ⁱ- <Н.Зб>

При холодной прокатке происходит упрочнение металла з зоне де­формации (наклеп), т. е. с возрастанием степени деформации от сече­ния А к сечению В соответственно возрастает предел текучести сг_т.

Для того чтобы учесть в дальнейшем влияние упрочнения (наклепа) на увеличение давления металла на валки при прокатке р_х, введем ко­эффициент упрочнения £:

L. ki/k₀ — Orjo-f., 1,

где От. — предел текучести материала полосы до прокатки (с учетом предшествующего упрочнения в предыдущих проходах при прокатке в

несколько пропусков); ст_т, —то же, после прокатки в данном проходе металла через валки.

Соответствующие значения а_т в зависимости от степени деформации приведены на рис. 1.15. Возвращаясь к выводу уравнений (П.о), (II.0), получим:

а) для зоны отставания (дуга Л/V), согласно уравнению (11.3), р.* = —p_A=k₀—;оо> поэтому С₀ = 1п(/г₀—сто) +2j.i{Ifho) и давление рх с уче­том внешнего натяжения cry равно

(II.5а)

б) для зоны опережения (дуга BN), согласно уравнению (II.3), при *=0 p_x=p_u — k\—ст|, поэтому C_t = ln(|^o—о\) и давление р" с учетом внешнего натяжения oi равно

(II.6а)

tn₀ 2 u///i₀; т_х 2₍ui//i₁.

Согласно полученным уравнениям (11.5а), (11.6а), от сечения входа

(где р"=р._л=/г₀—а₀) и от сечения выхода (где р" =рв = кi—а,) давл

ние металла на валки р" с учетом натяжений ао и oi по направлению к нейтральному сечению возрастает по экспоненциальным кривым (см. рнс. 11.7,6), аналогичным соответствующим кривым для случая прокатки без натяжения (см. рис. II.I), по с меньшими ординатами. Оче­видно, что давление при прокатке полосы с натяжением р" значительно меньше, чем при прокатке без натяжения р_х. Так как x_H<il/2, то заднее натяжение ао оказывает влияние на участке больше //2, т. е. заднее на­тяжение больше снижает полное давление Р, чем переднее натяжение 0|.

При обжатии е-<0,4 и упрочнен им £<1,2 можно принимать

(11.23)

и определять среднее давление при прокатке с натяжением по следую­щей формуле:

Pep — Pci) ^<1 — Pep (I °ср' ^с1>)»

где р_Ср — среднее давление при прокатке без натяжения; определяют по формулам (11.9), (П.11) или но кривым на рис. 11.3; а₍р— среднее на- тяжсиие полосы, равное (a₀+<Ti)/2; к_ср— средняя константа уравнения пластичности, равная (A’o4-/?i)/2 = 1,15 а_т._ср (здесь а_т.с_Р= (аг₀ + cf_t,)/2— средний предел текучести металла полосы, упрочняющегося при про­катке).

Из рассмотрения формулы (П.23) следует, что при больших натяже­ниях полосы давление металла на валки при прокатке значительно мень­ше, чем в случае прокатки без натяжения. Так, например, при а_ср= = 0,6 (&_Ср)~0,7 а_т.ср получим n_a —1—0,6 = 0,4 и р"_р = 0,4 р_(р, т. е. среднее давление при прокатке с таким натяжением в 2,5 раза меньше, чем при прокатке этой же полосы без натяжения. Этот пример показывает, что применение больших натяжении при холодной прокатке полисы являет­ся весьма желательным.

Практически по избежание частых разрывов полосы, которые могут происходить в процессе прокатки из-за мелких трещин (концентраторов напряжений), имеющихся на кромках полосы, натяжение при прокатке применяют в пределах ас._р= (0,3ч-0,6)£_гр« (0,35-^0,7)а_т.е_Р. При этом для получения лучшего качества поверхности готовой полосы, во избе­жание пробуксовки и уменьшения момента прокатки па валках (см. ни­же) обычно переднее удельное натяжение полосы принимают несколько больше заднего (т. е. ai>a₀).