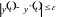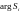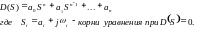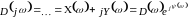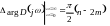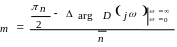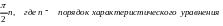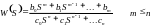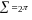Устойчивость линейных систем автоматического управления.

На любую автоматическую систему всегда действуют различные внешние возмущения, которые могут нарушить ее нормальную работу. Правильно спроектированная система должна устойчиво работать при всех внешних возмущениях.

Понятие устойчивости системы связано со способностью ее возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Если система неустойчива, то она не возвращается в состояние равновесия, из которого ее вывели.

Устойчива Неустойчива Безразлична Устойчива в молом, неустойчива в большом

Заданное движение системы при отсутствии возмущений называется невозмущенным движением.

Любое другое движение системы называет возмущенным

Заданное движение называется устойчивым, если после приложения возмущений, которые затем снимают возмущенное движение по истечении некоторого времени войдут в заданную область:

Теорема Ляпунова.

Для исследования систем на устойчивость необходимо получить характеристическое уравнение этой системы. При этом принципиально важны следующие теоремы.

Теорема 1.

Если вещественные части всех корней S_i характеристического уравнения первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво.

Теорема 2.

Если среди корней S_i характеристического уравнения первого приближения имеется хотя бы один корень с положительной вещественной частью, то невозмущенное движение неустойчиво.

Если невозмущенное движение устойчиво и при этом любое возмущенное движение при достаточно малых начальных возмущениях стремится к невозмущенному движению, то есть

где X_i(t) – возмущения.

То невозмущенное движение называют асимптотически устойчивым.

Характеристическое уравнение можно представить в следующем виде:

a_1,1-s а_1,2 ... а_1,n

а_2,1 а_2,2 - s... а_2,n

D (S) = = 0

а_n,1 а_n,2 ... а_n,n- s

Из него можно найти корни S_i , где i= 1,2,...,n.

В общем виде:

a_i,,w_i - вещественные и мнимые части корней.

Условия устойчивости линейных систем автоматического уравнения.

Дифференциальное уравнение линейной системы автоматического уравнения, записанное для регулируемой выходной величины x(t) при наличии управляющего воздействия g(t) имеет вид:

(a₀pⁿ +a₁p^n-1+...+a_n)x(t)=(b₀p^m+b₁p^m-1+...+b_m)(g)t (*)

где a₀,a₁,...,a_n и b₀,b₁,...b_m - постоянные коэффициенты

p= d/dt - оператор дифференцирования

Из него путем ряда преобразований можно получить характеристическое уравнение.

a₀sⁿ + a₁s^n-1+...+a_n=0 (**)

Нетрудно заметить, что левая часть уравнения (**) совпадает с дифференциальным оператором при выходной величине в уравнении (*).

Поэтому характеристическое уравнение получают приравняв этот оператор при выходной величине в исходном дифференциальном уравнении к нулю:

a₀pⁿ+a₁ p^n-1 +...+a_n =0 и заменив p=s

Решение этого уравнения содержит n корней.

В общем случае корни характеристического уравнения:

S_i= L_i+jw_i; L_i - вещественная часть;

w_i – мнимая часть;

Корни с отрицательными вещественными частями называют левыми, с положительными вещественными частями – правыми.

Условие устойчивости линейной системы:

Для того, чтобы линейная система была асимптотически устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения были левыми.

Критерии устойчивости.

Критерии устойчивости – это правила, которые позволяют определять устойчивость системы без вычисления корней. С их помощью можно установить устойчива система или нет, как влияют на устойчивость те или иные параметры и структурные изменения в системе.

Критерии устойчивости делятся на:

-алгебраические

-частотные.

Алгебраические критерии устойчивости

-Рауса

-Гурвица

-Льенара-Шипара

Частотные критерии устойчивости:

-Михайлова

-Найквиста

Алгебраические критерии устойчивости

Алгебраические критерии устойчивости позволяют судить об устойчивости системы по коэффициентам характеристического уравнения:

D(S) = a₀ sⁿ + a₁ s^n-1 + ... + a_n = 0

Необходимым условием устойчивости системы любого порядка является положительность всех коэффициентов характеристического уравнения:

a₀ > 0; a₁ > 0; ... ; a_n > 0

Для систем первого и второго порядков необходимое условие устойчивости является и достаточным условием устойчивости.

Из алгебраических критериев устойчивости наиболее широкое распространение получили критерии устойчивости Рауса и Гурвица. Они позволяют по коэффициентам характеристического уравнения без вычисления его корней сделать вывод об устойчивости системы.

Критерий устойчивости Рауса.

Этот критерий был предложен Э. Раусом в виде некоторого алгоритма, который просто поясняется следующей таблицей:

Коэффициент ri	Строка i	Столбец (k)
		1	2	3	4
-	1	a0 = c11	a2 = c21	a4 = c31	...
-	2	a1 = c12	a3 = c22	a5 = c32	...
	3	c13 = a2 – r3a3	c23 = a4 – r4a5	c33 = a6 – r3a7	...
	4	c14 = a3 – r4c23	c24 = a5 – r4c33	c34 = a7 – r4c43	...
	5	c15 = c­23 – r5c24	c25 = c33 – r5c34	c35 = c43 – r5c44	...
...	...	...	...	...	...
	i	c1, i = c2, i-1 – ric2, i-1			...

В первой строке записывают в порядке возрастания индексов коэффициенты характеристического уравнения, имеющие чётный индекс: а₀, а₂, а₄, а₆, ..., во второй строке – коэффициенты с нечётным индексом: а₁, а₃, а₅, а₇, ...

Любой из остальных коэффициентов таблицы определяется как:

c _{k, i} = c _{k+1, i-2} – r _i c _{k+1, i-1} ,

где

Здесь k – индекс, обозначающий номер столбца;

i – индекс, обозначающий номер строки таблицы.

Число строк таблицы Рауса равно степени характеристического уравнения плюс единица (n+1).

После того как таблица Рауса заполнится, по ней можно судить об устойчивости системы.

Условие устойчивости Рауса: для того, чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак, т.е. при а₀ > 0 были положительны:

c₁₁ = a₀ > 0; c₁₂ = a₁ > 0; c₁₃ > 0; ...; c_{1, n+1} > 0.

Если не все коэффициенты первого столбца положительны, то система неустойчива, а число правых корней характеристического уравнения равно числу перемен знака в первом столбце таблицы Рауса.

Пример.

Дано характеристическое уравнение:

W(S) = s⁶ + 6s⁵ +21s⁴ + 44s³ + 62s² + 52s + 100 = 0

Определить устойчива ли система.

Решение.

Составим таблицу Рауса:

Коэффициент ri	Строка i	Столбец (k)
		1	2	3	4
-	1	a0 = 1	a2 = 21	a4 = 62	a6 = 100
-	2	a1 = 6	a3 = 44	a5 = 52	a7 = 0
	3	c13=21-0,167 44=13,65	c23=62-0,16752=53,3	c33=100-0,167 0 = 100	0
	4	c14=44-0,4453,3=20,6	c24=52-0,44100=8	c34=0-0,44 0 = 0	0
	5	c15=53,3-0,688=48	c25=100-0,660=100	0	0
	6	c16=8-0,43100=-35	c26=0-0,430=0	0	0
	7	c17=100-(-1,37)0=100	0	0	0

Имеется две перемены знака коэффициентов первого столбца: следовательно, система неустойчива, а характеристическое уравнение имеет два правых корня.

Критерий Гурвица.

А. Гурвицем был разработан алгебраический критерий устойчивости в форме определителей, составляемых из коэффициентов характеристического уравнения системы.

Из коэффициентов характеристического уравнения строят сначала главный определитель Гурвица

по следующему правилу: по главной диагонали слева направо выписывают все коэффициенты характеристического уравнения от а₁ до а_n в порядке возрастания индексов. Столбцы вверх от главной диагонали дополняют коэффициентами характеристического уравнения с последовательно возрастающими индексами, а столбцы вниз – коэффициентами с последовательно убывающими индексами. На место коэффициентов с индексами больше n и меньше нуля проставляют нули. (n – порядок характеристического уравнения).

Из главного определителя Гурвица получаем определители Гурвица низшего порядка:

Δ₁ = а₁; ; ; ...;

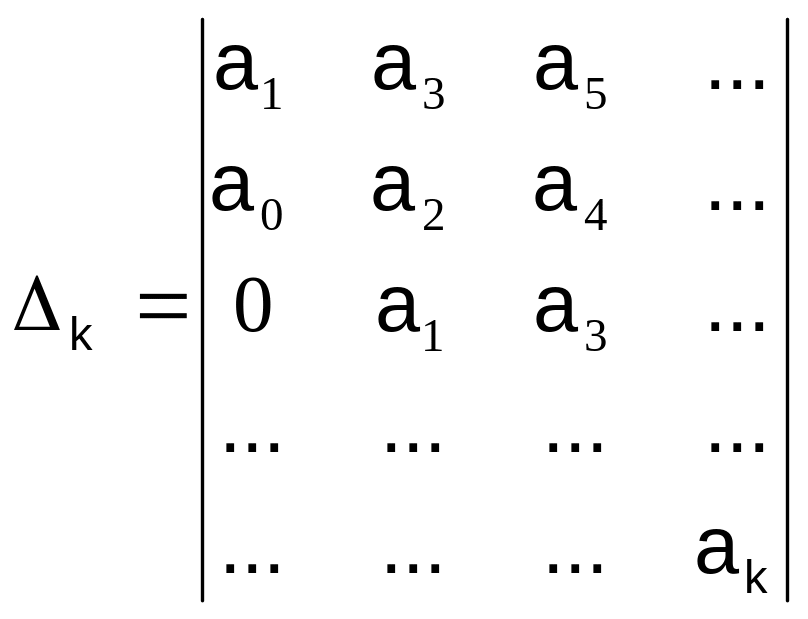
Номер определителя Гурвица определяется номером коэффициента по диагонали, для которого составляют данный определитель. Критерий устойчивости Гурвица формулируется так: для того, чтобы система автоматического управления была устойчива необходимо и достаточно, чтобы все определители Гурвица имели знаки, одинаковые со знаком первого коэффициента характеристического уравнения а₀, т.е. при а₀ > 0 были положительными.

Таким образом, при а₀ > 0 для устойчивости системы необходимо и достаточно выполнения следующих условий:

Δ₁ = a₁ > 0; Δ₂ = > 0; Δ₃ = > 0; ...;

Δ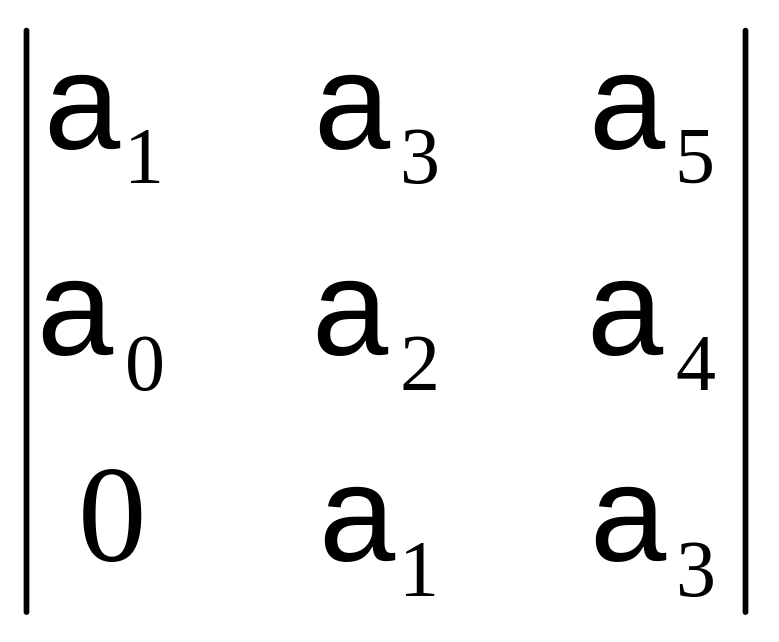_n = > 0

Раскрывая определители Гурвица для характеристических уравнений первого, второго, третьего и четвёртого порядка, можно получить следующее условие устойчивости:

1. Для уравнений первого порядка (n = 1), т.е. а₀s + a₁ = 0, условия устойчивости:

а₀ > 0; a₁ >0

2. Для уравнений второго порядка (n = 2), т.е. a₀s² + a₁s + a₂ = 0, условия устойчивости:

а₀ > 0; a₁ > 0; a₂ > 0

3. Для уравнений третьего порядка (n = 3), т.е. a₀s³ + a₁s² + a₂s + a₃ = 0, условия устойчивости:

а₀ > 0; a₁ > 0; a₂ > 0; a₃ > 0;

a₁a₂ – a₀a₃ > 0

4. Для уравнений четвёртого порядка (n = 4), т.е. a₀s⁴ + a₁s³ + a₂s² + a₃s + a₄ = 0, условия устойчивости:

а₀ > 0; a₁ > 0; a₂ > 0; a₃ > 0; а₄ > 0;

a₃ (a₁a₂ – a₀a₃) – a₄ > 0

Таким образом, необходимым и достаточным условием устойчивости для систем первого и второго порядков является положительность коэффициентов характеристического уравнения. Для уравнения третьего и четвёртого порядков кроме положительности коэффициентов необходимо соблюдение дополнительных неравенств.

При число дополнительных неравенств возрастает, процесс раскрытия определителей становиться трудоёмким. Поэтому критерий устойчивости обычно применяют при . В последнем столбце главного определителя Гурвица отличен от нуля только один коэффициент a_n, поэтому

Δ_n = a_n Δ_n-1

При a_n > 0 для проверки устойчивости систем достаточно найти только определители Гурвица от Δ₁ до Δ_n-1. Если все определители Гурвица низшего порядка положительны, то система находиться на границе устойчивости, когда главный определитель равен нулю:

Δ_n = a_n Δ_n-1

Это равенство возможно в двух случаях: a_n = 0 или Δ_n-1 = 0. В первом случае система находиться на границе апериодической устойчивости; во втором случае – на границе колебательной устойчивости.

Используя критерий Гурвица, можно при заданных параметрах системы принимать за неизвестный какой-либо один параметр и определить его предельное (критическое) значение, при котором система будет находиться на границе устойчивости.

Частотные критерии устойчивости.

Они позволяют судить об устойчивости систем автоматического управления по виду их частотных характеристик

В основе частотных критериев устойчивости лежит следствие из принципа аргумента.

Пусть дано характеристическое уравнение:

D(S)=a₀Sⁿ+a₁S^n-1+...a_n

Его можно представить в виде:

D(S)=a₀(S-S₁)(S-S₂)...(S-S_n)

Где S_i=a_i+jw_i - корни уравнения D(S)=0.

На комплексной плоскости S каждый корень геометрически может быть изображен вектором, проведенным из начала координат к точке S_i. Длина этого вектора равна модулю комплексного числа S_i, а угол поворота равен аргументу комплексного числа.

Пусть уравнение имеет n равных корней. (n-m) - количество левых корней.



Будет справедливо следующее правило:

^{Изменение (приращение) аргумента D(jw) при изменении частоты w от до равно разности между числом левых и правых корней уравнения D(S)=0, умноженной на n}-

При изменении частоты w от нуля до бесконечности изменение аргумента будет в два раза меньше:

Критерий устойчивости Михайлова.

Кривая, то есть годограф Михайлова, строится следующим образом. Из знаменателя передаточной функции составляется характеристическое уравнение.

На комплексной плоскости S каждый корень геометрически может быть изображен вектором, проведенным из начала координат к точке S_i.

Таким образом, пусть дано характеристическое уравнение. Если подставить в этот полином чисто линейное значение

то получим комплексный полином.

При изменении частоты w вектор D(jw) изменяясь по величине и направлению, будет описывать своим концом в комплексной плоскости

некоторую кривую (годограф Михайлова).

Угол поворота вектора D(jw) вокруг начала координат при изменении частоты w от нуля до бесконечности равен:

Откуда число правых корней полинома D(S), то есть

Таким образом, число правых корней будет равно нулю при условии:

Это условие является необходимым, но не достаточным. Для устойчивости системы необходимо и достаточно, чтобы все n коней характеристического уравнениями были левыми. Иначе говоря, среди них не должно быть корней, лежащих на левой оси и обращающих в ноль комплексный полином, D(jw) то есть должно выполняться еще одно условие:

Таким образом, критерий Михайлова: для того, чтобы система автоматического уравнения была устойчива необходимо и достаточно, чтобы вектор кривой Михайлова D(jw) при изменении w от нуля до бесконечности повернулся, нигде не обращаясь в ноль, вокруг начала координат против часовой стрелки на угол

Задана следующая кривая (строится по знаменателю передаточной функции)

Мнимая ось Действит.ось

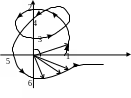
n=8 – степень характеристического уравнения

Определить устойчива ли система.

То есть, была задана некая передаточная функция W(S)=-....

Рассматриваем знаменатель ее D(S)...

Заменяем S=jw. Разбиваем на действительную и мнимую части. Строим график по этому уравнению, разбивая w от 0 до .

Решение.

Обозначим точки пересечения кривой с осями по ходу увеличения величины (от 0 до ). Получили точки (1,2,3,4,5,6,7 (в )). При дальнейшем увеличении кривая будет параллельна какой – либо оси.

Рассматривая каждый участок, смотрим как меняется при этом аргумент.

1-2: (поворот вектора против часовой стрелки, т.е. положительный поворот)

меняется от нуля до

2-3: 0 (вектор отклонился и вновь вернулся, т.е. поворот вектора равен нулю)

Рассматривая участки, мы рассматриваем уменьшение частоты от начального до конечного. Разность их - это и есть изменение.

3-4: 0

4-5;

5-6;

6-7: (точка 7 в . Сначала угол из точки 6 увеличивается и в точке 7 он будет равен )

М ы нашли изменения угла поворота вектора от 0 до . Сложим углы и получим:

Опять рассмотрим определение устойчивости по Михайлову (вектор должен поворачиваться на угол ).

У нас n=8

Значит система неустойчива. Тогда, можем найти число правых корней этой системы (если система неустойчива).

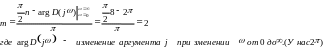
Следовательно, система неустойчива и число правых корней равно 2.

Критерий Найквиста.

Этот критерий позволяет судить об устойчивости замкнутой системы по виду А-Ф (амплитудно- фазовой) характеристики разомкнутой системы.

Если передаточная функция разомкнутой системы

Представляя S=jw получаем частотную передаточную функцию разомкнутой системы.

Если изменить частоту w от до , то вектор будет меняться по величине и фазе. Кривую, описываемую концом этого вектора в комплексной плоскости, называют амплитудно-фазовой характеристикой разомкнутой системы.

При каких условиях замкнутая система будет устойчива?

(Она будет устойчива, если разомкнутая система неустойчива и имеет l правых корней.)

Существует 2 способа определения правых корней:

1) Можно считать охваты.

2) Можно использовать правило перехода Ципкина.

1) Таким образом, критерий Найквиста: если разомкнутая система автоматического управления неустойчива, то для того чтобы замкнутая система автоматического управления была устойчива, необходимо и достаточно , чтобы А-Ф характеристика разомкнутой системы при изменении частоты от 0 до охватывала точку(-1; j0) в положительном направлении раз, где – число правых корней характеристического уравнения разомкнутой системы.

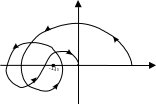
Дана частотная характеристика разомкнутой системы.

j 4 2 5 3 1 w=0

Будем считать поворот вектора. Расставим точки на пересечении кривой с действительной осью (получилось 6 точек). Будем рассматривать повороты вектора с началом в точке (-1; j0) .Получим участки:

1-2: (угол поворота равен )

2-3:

3-4:

4-5: 0 (т. к. Вектор начинает поворачиваться и возвращается в то же положение)

5-6: - (т.к. вектор поворачивается по часовой стрелке)

На основе принципа аргумента изменения угла поворота вектора при изменении частоты от до (только при положительных частотах).

где – число правых корней характеристического уравнения разомкнутой системы.

Таким образом, в нашем случае

-число правых корней

Таким образом, вывод: замкнутая система будет устойчива если разомкнутая система будет иметь 2 правых корня.

2. Используя правило Ципкина

J + + - w=0

Рассмотрим участок от до (-1; j0) и ставим (+) и (-) (положительные, и отрицательные переходы)

Если кривая пересекает действительную ось слева от точки (-1; j0) против часовой стрелки, т. е. сверху вниз, то ставим знак «+». Если по часовой стрелке, т.е. снизу вверх, то ставим знак «-» . Подсчитываем количество знаков. У нас получилось +,+,-.

2(+)-1(-)=1/2

Следовательно, система будет устойчива, если разомкнутая система имеет 2 правых корня.