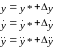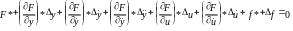- •Представим объект управления в виде прямоугольника
- •Принципы управления.
- •Основные виды автоматического управления.
- •Основные законы регулирования.
- •Пропорциональный закон (п-закон)
- •И нтегральный закон (и-закон)
- •П ропорционально – интегральный закон (пи-закон)
- •4.Пропорционально – интегрально - дифференциальный закон (пид-закон)
- •Понятие о модификации.
- •Преобразование Лапласа.
- •Понятие о передаточной функции.
- •Частотные характеристики.
- •Временные характеристики.
- •Элементарные звенья.
- •Преобразование структурных схем
- •Устойчивость линейных систем автоматического управления.
- •Теорема Ляпунова.
- •Условия устойчивости линейных систем автоматического уравнения.
И нтегральный закон (и-закон)
Tи –постоянная времени интегрирования
П ропорционально – интегральный закон (пи-закон)
|
При Ти>>0 закон становится пропорциональным.
4.Пропорционально – интегрально - дифференциальный закон (пид-закон)
|
kp a
|
ТД - постоянная времени дифференцирования.
Понятие о модификации.
При разработке и исследовании автоматической системы управления получают ее математическое описание. Оно может быть:
аналитическим
графическим
табличным
Математическая модель – это запись математических уравнений, описывающих процессы, происходящие в изучаемых объектах.
В основном эти уравнения являются нелинейными дифференциальными уравнениями. Например, рассмотрим звено,
-


 f
f
u y
которое можно описать дифференциальным уравнением второго порядка
![]() (1)
(1)
Где y – выходная величина
u, f – входные величины
![]() - первая производная по времени
- первая производная по времени
![]() - вторая производная по времени
- вторая производная по времени
Это уравнение при произвольных входных воздействиях называют уравнением динамики.
П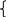
 усть
при постоянных входных величинах
u=u*
усть
при постоянных входных величинах
u=u*
f=f*
процесс в звене с течением времени установится так, что выходная величина примет постоянное значение y=y*
Тогда уравнение (1) примет вид:
F(y*,0,0,u*,0)+f*=0 (2)
Это уравнение описывает статистический режим и называется уравнением статики.
Статистический режим можно описать графически с помощью статических характеристик.
Статическая характеристика – это зависимость выходной величины от входной в статическом режиме.
x2вх y2вых x1вх y1вых yвх t y2вых x1вх x2вх xвх
Статическая y1вых характеристика t t Динамические характеристики
|
В общем случае реальные значения отклонений
от номинальных обозначим через y,
u,..., Тогда
общем случае реальные значения отклонений
от номинальных обозначим через y,
u,..., Тогда
u
u
u
f
f
f
u
u
u
*
*
*
|
Подставим эти выражения в формулу(1) и разложим функцию в ряд Тейлора. Тогда:
В ычтем из этого уравнения уравнение (1), получим:
|
Где:
|
Полученное уравнение (3) возможно при следующих условиях:
отклонения выходной y и входной u величин малы.
Функция F должна быть дифференцируема по всем переменным.
Это уравнение является линейным относительно приращений.
Если
полученные производные
![]() не зависят от времени, то ai
и bi
- постоянные
величины, то уравнение (3) является
линейным относительно приращений с
постоянными коэффициентами.
не зависят от времени, то ai
и bi
- постоянные
величины, то уравнение (3) является
линейным относительно приращений с
постоянными коэффициентами.
В теории уравнения для облегчения решения линейных дифференциальных уравнений применяются преобразования Лапласа.


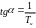
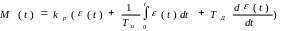




 t
t














 yвых
xвх
yвых
xвх