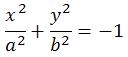15. Равенство характеристических многочленов подобных матриц.

А

В: Р^-1АР

16. Ортогональность собственных векторов, соответствующих различным собственным значениям самосопряженного линейного преобразования.

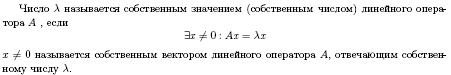
Будем вести индукцию по n. В случае n=1 любое преобразование имеет вид

Поэтому любой ненулевой вектор х является собственным, и доказывать нечего.

Предположим, что утверждение теоремы верно для симметрических преобразований в евклидовом пространстве размерности n-1, и в этом предположении докажем его для евклидова пространства размерности n.

Прежде всего возьмем какое-либо собственное значение λ₁ симметрического преобразования f. По теореме о действительности корней уравнения симметрической матрицы λ₁ – действительно число. Пусть а₁ – соответствующий собственный вектор.

Обозначим через S – множество всех векторов , ортогональных к а₁

Так как подпространство S есть ортогональное дополнение к линейной оболочке L(а₁), то его размерность равна n-1. Покажем, что это подпространство выдерживает действие f. Это означает, что если , то . Действительно,

Из сказанного следует, что действие f на всем пространстве V можно при желании сузить до действия f на подпространстве S. Применяя предположение индукции, получим, что в S существует ортогональный базис , состоящий из собственных векторов преобразования, т.е.

Вместе с равенством это доказывает нашу теорему.

17. Изменение матрицы квадратичной формы при замене базиса.

, где х – вектор-столбец.

Х=РY

|P|≠0, B=P^TAP

 =Y^TBT

20. Выпуклость пересечения выпуклых множеств Лемма: Пересечение нескольких выпуклых множеств есть выпуклое множество.

Доказательство. Пусть М = LÇN, где L, N выпуклы.

Пусть АÎM и BÎМ => AÎL и BÎL.

L выпуклое => [А,В] Ì L.

Пусть АÎM и BÎМ => AÎN и BÎN.

N выпуклое => [А,В] Ì N.

=> [А,В] Ì М => М - выпуклое.

14(411)Матрица перехода от базиса к базису. Преобразование координат вектора при переходе к новому базису.

n – мерное пространство.

V_n – базис, состоящий из n векторов.

В пространстве есть базисы

Введем матрицу перехода от к .

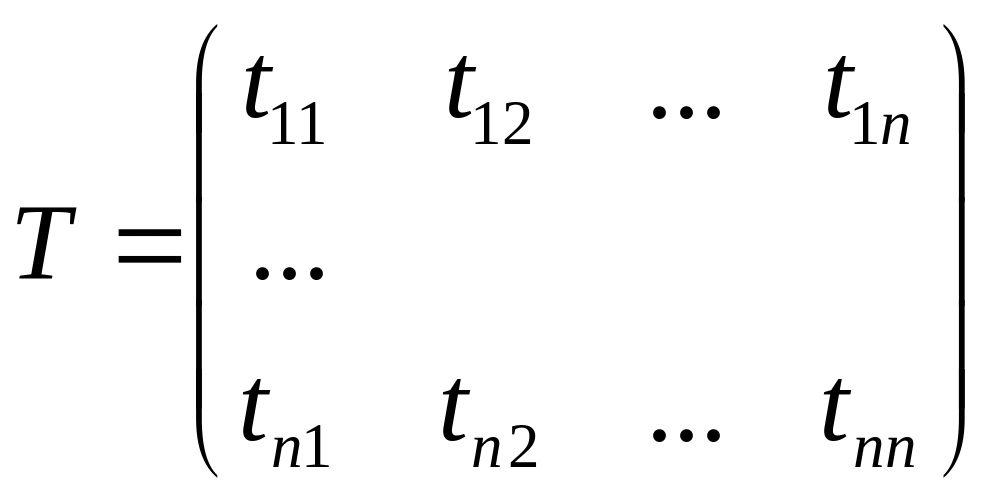
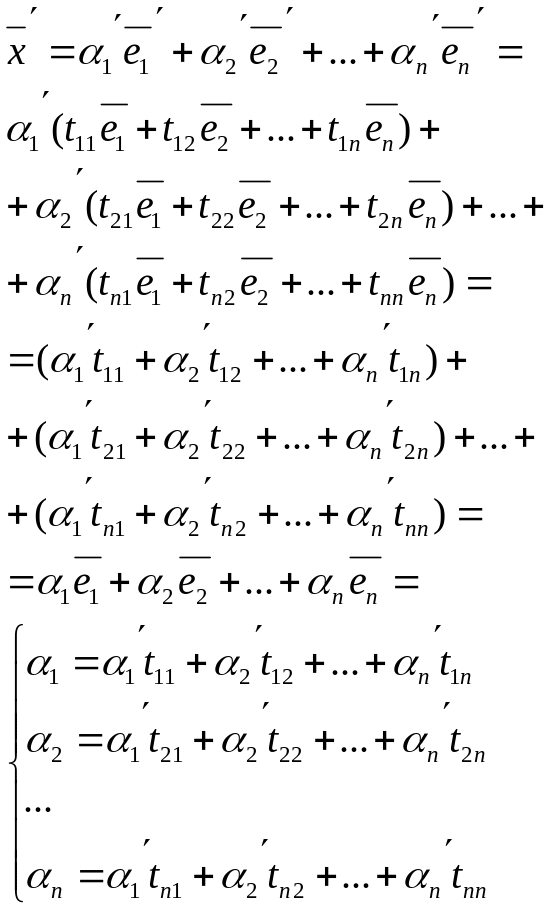
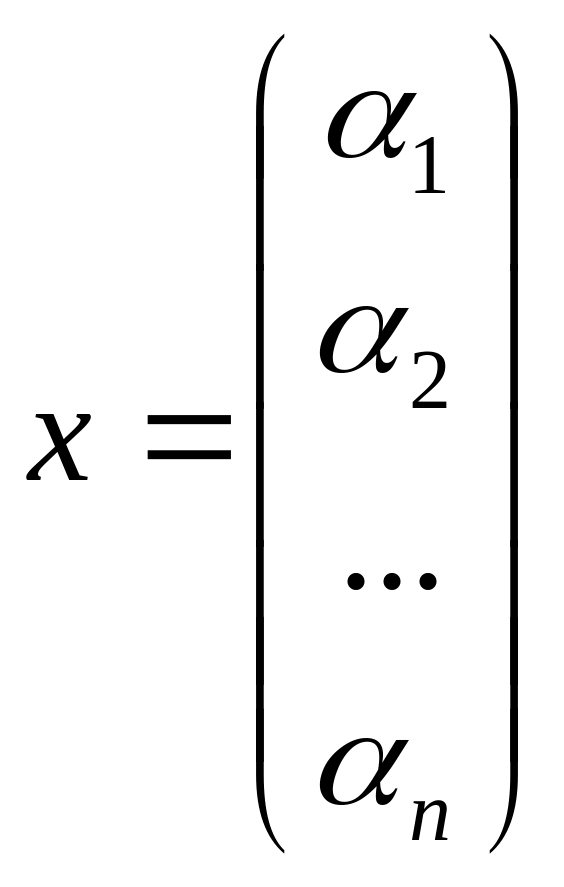
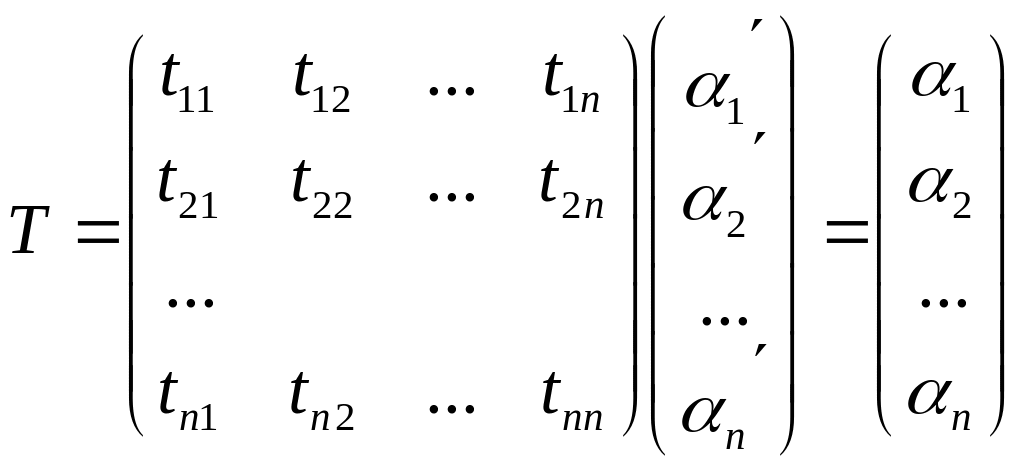
19(416) Эллипс. Определение. Вывод канонического уравнения.

Э ллипсом называется

геометрическое место всех

точек плоскости, сумма

расстояний от которых до

до фокусов есть величина

постоянная, большая, чем расстояние между фокусами.

Пусть М (х;у) – произвольная точка эллипса.

Т.к. MF₁ + MF₂ = 2a

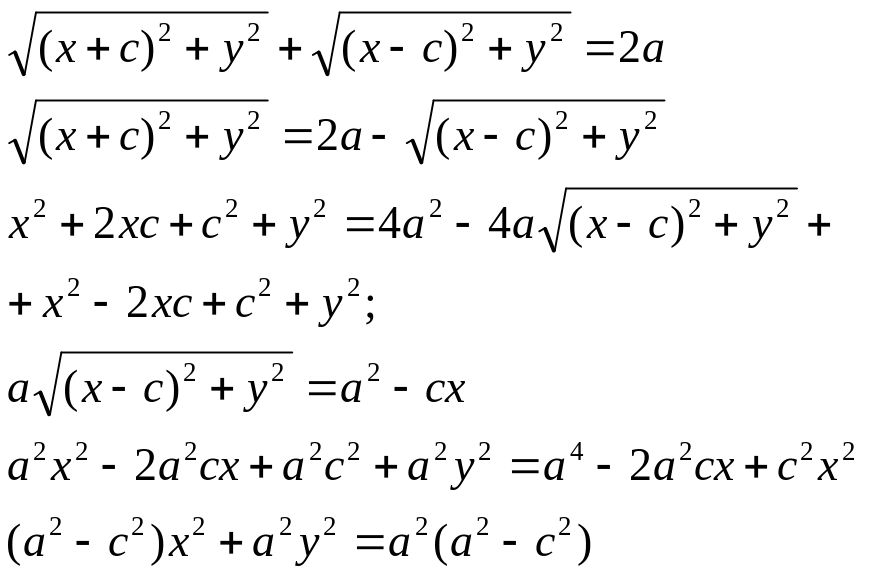
Т.к.

То получаем

Или

20(417)Гипербола. Определение. Вывод канонического уравнения.

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до фокусов есть величина постоянная.

Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы |MF₁ – MF₂|=2a или MF₁ – MF₂=±2a,

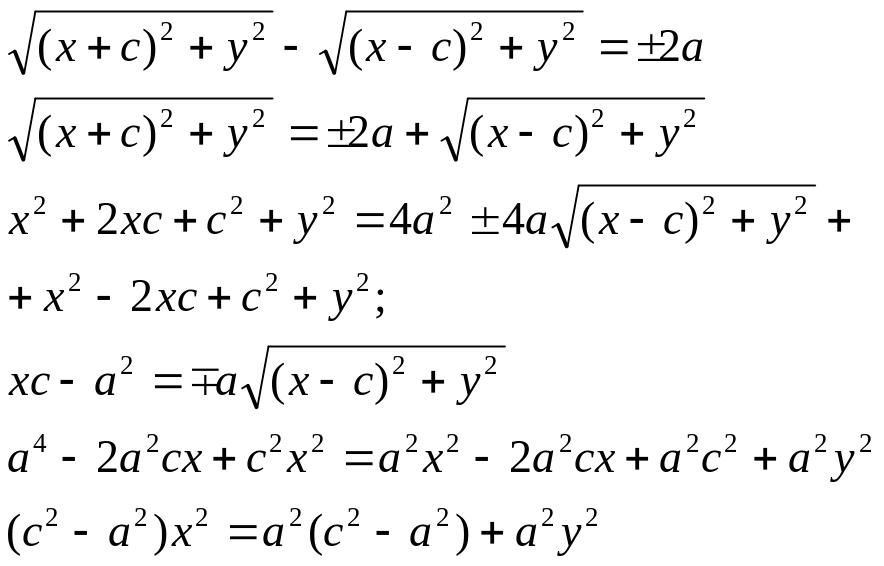
Кривые 2 порядка

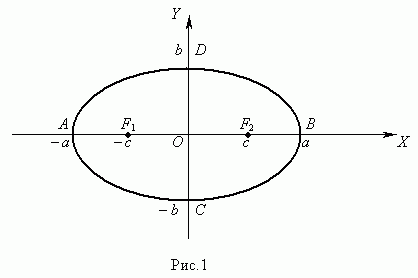
Уравнение эллипса ( рис.1 ) :

Здесь начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При a > b фокусы эллипса лежат на оси ОХ ( рис.1 ) , при a < b фокусы эллипса лежат на оси ОY , а при a = b эллипс становится окружностью ( фокусы эллипса в этом случае совпадают с центром окружности ). Таким образом, окружность есть частный случай эллипса.

Отрезок F1F2 = 2 с , где , называется фокусным расстоянием. Отрезок AB = 2 a называется большой осью эллипса, а отрезок CD = 2 b – малой осью эллипса. Число e = c / a , e < 1 называется эксцентриситетом эллипса.

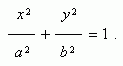
Гипербола. Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных фиксированных точек (фокусов) гиперболы есть одна и та же постоянная величина. Предполагается, что эта постоянная величина не равна нулю и меньше, чем расстояние между фокусами.

Простейшее уравнение гиперболы

Здесь a - действительная полуось гиперболы, b - мнимая полуось гиперболы.

Если 2c - расстояние между фокусами гиперболы, то между a, b и c существует соотношение

a2 + b2 = c2.

При b = a гипербола называется равносторонней. Уравнение равносторонней гиперболы имеет вид

x2 - y2 = a2.

Фокусы гиперболы лежат на ее действительной оси.

Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к длине ее действительной оси.

Парабола. Параболой называется геометрическое место точек, каждая из которых одинаково удалена от заданной фиксированной точки и от заданной фиксированной прямой. Точка, о которой идет речь в определении, называется фокусом параболы, а прямая - ее директрисой.

Простейшее уравнение параболы

y2 = 2px. (*)

Входящая в это уравнение величина p называется параметром параболы. Параметр параболы равен расстоянию от директрисы параболы до ее фокуса.

Координаты фокуса F параболы (*) . (фокус параболы лежит на ее оси симметрии) Уравнение директрисы параболы (*)

Эксцентриситет параболы e = 1.

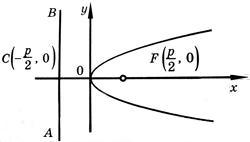
y2 = 2px (p > 0)

Две пересекающиеся прямые

Две параллельные прямые

Двукратная(одна) прямая

x2 = 0

Мнимые параллельные прямые

Мнимые пересекающиеся прямые

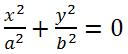
Мнимый эллипс