
- •1 Вопрос
- •1.1.1. Основные понятия и аксиомы статики
- •Различают три группы связей:
- •1. Гибкие связи (трос, цепь, ремень, канат). Реакции связей направлены по оси связей (рис. 1.8).
- •2. Твердые, идеально гладкие связи. Реакция направлена по общей нор-мали к поверхностям
- •3. Шарнирные связи. Шарниром в механике называется устройство, до-пускающее поворот одного тела
- •2 Вопрос
- •Виды опор
- •Внешние силы
- •Внутренние силы
- •3 Вопрос Проэкция силы на ось и плоскость
- •4 И 5.Сложение двух сил.Сложение трех сил, не лежащих в одной плоскости. Равнодействующая.
- •6.Вектор момента силы относительно центра.Момент силы относительно оси.
- •7. Лемма о параллельном переносе силы
- •Основная теорема статики
- •8. Условия равновесия пространственной системы сил
- •Привидение плоской системы сил к простейшему виду
- •9. Привидение плоской системы сил к простейшему виду
- •11. Однофазный синусоидальный ток и его характеристика.
- •13. Определение скорости и ускорения точки при естественном задании движения
- •14. Поступательное движение твердого тела. Вращательное движение тела: способы задания, угловая скорость и угловое ускорение.
- •15. Скорости и ускорения точек вращающегося тела.
- •22 Вопрос ... Свободные колебания материальной точки без учета сил сопротивления. Дифференциальное уравнение гармонических колебаний и его решение.
- •23 Вопрос ... Влияние сил сопротивления на свободные колебания точки. Апериодическое движение.
- •24 Вопрос.. Вынужденные колебания без учета сил сопротивления. Дифференциальное уравнение вынужденных колебаний и его интегрирование. Резонанс.
- •Колебаний, имеющих собственную частоту k , амплитуда которых определяется воздействием возмущающей силы и не зависит от начальных условий:
- •Вынужденных колебаний, происходящих с частотой возмущающей силы и не зависящих от начальных условий:
- •Вопрос 31. Прочность, жесткость, устойчивость.Задачи сопротивления материалов.
- •Вопрос 32.Класификацияч сил действующих на элементы конструкции
- •33 Вопрос. Понятие о деформации.Основные виды дифоормации.Диформации линейные и угловые ,абсолютные и относительные .Продолные и поперечные диформации.
- •34. Понятие о напряжениях
- •35. Внутренние силы. Внутренние силовые факторы и их эпюры. Алгоритм построения эпюр
- •36. Расчетная схема.Изображение расчетной схемы. Деление на силовые участки
- •40. Основные характеристики прочности.
- •Условный предел текучести
- •41. Геометрические характеристики плоских сечений.
- •42.Деформация сдвига. Условия прочности при расчете на срез, на смятие, на разрыв.
- •43.Кручение.
- •44. Расчеты на прочность и жесткость при кручении.
- •4. Условие жесткости при растяжении (сжатии) записывается в виде
9. Привидение плоской системы сил к простейшему виду
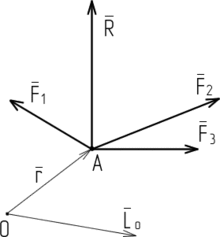
Рассмотрим систему сил (F1, F2,..., Fn), расположенных в одной плоскости. Совместим с плоскостью расположения сил систему координат Оху и, выбрав ее начало в качестве центра приведения, приведем рассматриваемую систему сил к одной силе F0=åFk, (5.1) равной главному вектору, и к паре сил, момент которой равен главному моменту M0=åM0(Fk), (5.2) где Мо(Fk)– момент силы Fk относительно центра приведения О. Так как силы распол в одной пл-ти, то сила Foтакже лежит в этой плоскости. Момент пары Мо направлен перпендикулярно этой плоскости, т.к. сама пара распол в пл-ти действия рассматриваемых сил. Т.о., для плоской системы сил главный вектор и главный момент всегда перпендикулярны друг другу (рис. 5.1). Момент полностью характеризуется алгебраической величиной Mz, равной произведению плеча пары на величину одной из сил, составляющих пару, взятой со знаком плюс, если «вращение-» пары происходит, против хода часовой стрелки, и со знаком минус, если оно происходит по ходу часовой стрелки. Пусть, например, даны две пары, (F1, F`1) и (F2, F`2) (рис. 5.2); тогда согласно данному определению имеем Mz(F1,F`1)=h1F1, MZ(F2,F'2)=-h2F2. Моментом силы относительно точки будем называть алгебраическую величину, равную проекции вектора момента силы относительно этой точки на ось, перпендикулярную плоскости, т. е. равную произведению модуля силы на плечо, взятому с соответствующим знаком. Для случаев, изображенных на рис. 5.3, а и б, соответственно будет Moz(F1)=hF1, Moz(F2)=–hF2 (5.4). Индекс z в формулах (5.3) и (5.4) сохранен для того, чтобы указать на алгебраический характер моментов. Модули момента пары и момента силы обозначаются следующим образом: М(F,F')=| Мz(F,F`)|, Мо(F)=|МОz(F)|. Получим, Moz=åMoz(Fz). Для аналитического определения главного вектора применяются формулы: Fox=åFkx=F1x+F2x+…+Fnx, Foy=åFky=F1y,+F2y+…+Fny, Fo=(F2ox+F2oy)1/2=([åFkx]2+[åFky]2)1/2 (5.8); cos(x, Fo)=Fox /Fo, cos(y, Fo)=FOy/Fo.(5.9). А главный момент равен МОz=åMOz(Fk)=å(xkFky–ykFkx), (5.10) где xk, yk– координаты точки приложения силы Fk.
Докажем, что если главный вектор плоской системы сил не равен нулю, то данная система сил эквивалентна одной силе, т. е. приводится к равнодействующей. Пусть Fo≠0, МОz ≠0 (рис. 5.4, а). Дуговая стрелка на рис. 5.4, а символически изображает пару с моментом MOz. Пару сил, момент которой равен главному моменту, представим в виде двух сил F1 и F`1, равных по модулю главному вектору Fo, т. е. F1=F`1 =Fo. При этом одну из сил (F`1), составляющих пару, приложим к центру приведения и направим в сторону, противоположную направлению силы Fo (рис. 5.4, б). Тогда система сил Fo и F`1 эквивалентна нулю и может быть отброшена. Следовательно, заданная система сил эквивалентна единственной силе F1 приложенной к точке 01; эта сила и является равнодействующей. Равнодействующую будем обозначать буквой R, т.е. F1=R. Очевидно, что расстояние h от прежнего центра приведения О до линии действия равнодействующей можно найти из условия |MOz|=hF1 =hFo, т.е. h=|MOz|/Fo. Расстояние h нужно отложить от точки О так, чтобы момент пары сил (F1, F`1) совпадал с главным моментом MOz (рис. 5.4, б). В результате приведения системы сил к данному центру могут встретиться следующие случаи: (1) Fo≠0, MOz≠0.В этом случае система сил может быть приведена к одной силе (равнодействующей), как это показано на рис. 5.4, в.(2) Fo≠0, МОz=0. В этом случае система сил приводится к одной силе (равнодействующей), проходящей через данный центр приведения. (3) Fo=0, MOz≠0. При этом система сил эквивалентна одной паре сил. (4) Fo=0, МОz=0. В этом случае рассматриваемая система сил эквивалентна нулю, т. е. силы, составляющие систему, взаимно уравновешены.
Теоре́ма Вариньо́на — одна из теорем механики, устанавливающая зависимость между моментами сил данной системы и моментом их равнодействующей силы относительно какого-либо центра или оси. Сформулирована для сходящихся сил Пьером Вариньоном в 1687, либо, ещё раньше, Симоном Стевином.
Теорема Вариньона:
-
Если система сил, приложенных к абсолютно твердому телу имеет равнодействующую, то момент равнодействующей относительно произвольного центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси).
Векторная запись теоремы:
![]() .
.
10.
Изображение синусоидальных ЭДС,
напряжений
и
токов на плоскости декартовых
координат
![]()
![]() Синусоидальные
токи и напряжения можно изобразить
графически, записать при помощи уравнений
с тригонометрическими функциями,
представить в виде векторов на декартовой
плоскости или комплексными
числами.
Приведенным
на рис. 1, 2 графикам двух синусоидальных
ЭДС е1ие2соответствуют
уравнения:
Синусоидальные
токи и напряжения можно изобразить
графически, записать при помощи уравнений
с тригонометрическими функциями,
представить в виде векторов на декартовой
плоскости или комплексными
числами.
Приведенным
на рис. 1, 2 графикам двух синусоидальных
ЭДС е1ие2соответствуют
уравнения:
![]()
![]() .
Значения
аргументов синусоидальных
функций
.
Значения
аргументов синусоидальных
функций ![]() и
и ![]() называются фазами синусоид,
а значение фазы в начальный момент
времени (t=0):
называются фазами синусоид,
а значение фазы в начальный момент
времени (t=0): ![]() и
и ![]() - начальной
фазой (
- начальной
фазой (![]()
![]() ).
).
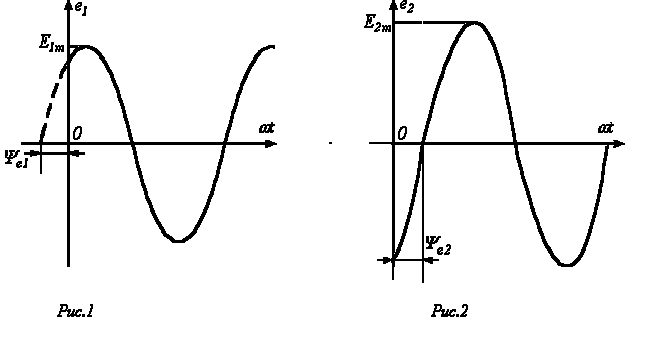 Величину
Величину ![]() ,
характеризующую скорость изменения
фазового угла, называют угловой
частотой. Так
как фазовый угол синусоиды за время
одного периода Т изменяется
на
,
характеризующую скорость изменения
фазового угла, называют угловой
частотой. Так
как фазовый угол синусоиды за время
одного периода Т изменяется
на ![]() рад.,
то угловая частота есть
рад.,
то угловая частота есть![]() ,
где f
– частота.
При
совместном рассмотрении двух синусоидальных
величин одной частоты разность их
фазовых углов, равную разности начальных
фаз, называют углом
сдвига фаз.
Для
синусоидальных ЭДС е1ие2угол
сдвига фаз:
,
где f
– частота.
При
совместном рассмотрении двух синусоидальных
величин одной частоты разность их
фазовых углов, равную разности начальных
фаз, называют углом
сдвига фаз.
Для
синусоидальных ЭДС е1ие2угол
сдвига фаз:
![]() .
.
Векторное изображение изменяющихся величин
Определение
амплитуды ![]() и
начальной фазы
и
начальной фазы ![]() этого
тока путем соответствующих тригонометрических
преобразований получается довольно
громоздким и мало наглядным, особенно,
если суммируется большое число
синусоидальных величин. Значительно
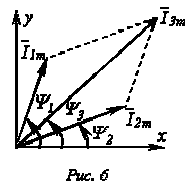
проще это осуществляется с помощью
векторной диаграммы. На рис. 6 изображены
начальные положения векторов токов,
проекции которых на ось ординат дают
мгновенные значения токов для t
= 0. При
вращении этих векторов с одинаковой
угловой скоростью w их
взаимное расположение не меняется, и
угол сдвига фаз между ними остается
равным
этого
тока путем соответствующих тригонометрических
преобразований получается довольно
громоздким и мало наглядным, особенно,
если суммируется большое число
синусоидальных величин. Значительно
проще это осуществляется с помощью
векторной диаграммы. На рис. 6 изображены
начальные положения векторов токов,
проекции которых на ось ординат дают
мгновенные значения токов для t
= 0. При
вращении этих векторов с одинаковой
угловой скоростью w их
взаимное расположение не меняется, и
угол сдвига фаз между ними остается
равным
![]() .
.
 Так
как алгебраическая сумма проекций
векторов на ось ординат равна мгновенному
значению общего тока, вектор общего
тока равен геометрической сумме векторов
токов:
Так
как алгебраическая сумма проекций
векторов на ось ординат равна мгновенному
значению общего тока, вектор общего
тока равен геометрической сумме векторов
токов:
![]() .
Построение
векторной диаграммы в масштабе позволяет
определить значения
и
из
диаграммы, после чего может быть записано
решение для мгновенного значения
.
Построение
векторной диаграммы в масштабе позволяет
определить значения
и
из
диаграммы, после чего может быть записано
решение для мгновенного значения ![]() путем
формального учета угловой частоты:
путем
формального учета угловой частоты: ![]() .
.
