41. Геометрические характеристики плоских сечений.

Моменты сопротивления

Осевой момент сопротивления относительно рассматриваемой оси – величина равная моменту инерции относительно той же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки

;  .                                                        

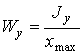Полярный момент сопротивления

                                                       

Осевой и полярный моменты инерции имеют размерность м³.

 

Поперечное сечение стержня представляет собой плоскую фигуру, для которой определяют некоторые геометрические характеристики, простейшей из которых является площадь, обозначаемая буквой А (рис. 4.1).

Статическим моментом площади относительно оси называется сумма произведений элементарных площадок dA на их расстояния до этой оси, взятая по всей площади.

Статические моменты площади относительно осей х и у.

,    .

Обычно статические моменты площади измеряют в кубических сантиметрах (см³).

Статические моменты площади могут быть положительными, отрицательными и равными нулю. Оси, относительно которых статические моменты площади равны нулю, называются центральными осями. Все такие оси проходят через одну точку – центр тяжести фигуры.

Статический момент площади относительно некоторой оси равен произведению площади на расстояние от центра тяжести до этой оси

;   .

 Моменты инерции площади

Осевым моментом инерции площади называется сумма произведений элементарных площадок dA на квадраты их расстояний до выбранной оси, взятая по всей площади:

 ;     .

Полярным моментом инерции площади относительно выбранной точки (полюса) называется сумма произведений элементарных площадок dA на квадраты их расстояний до полюса, взятая по всей площади:

.

Поскольку то полярный момент инерции равен сумме осевых моментов инерции относительно взаимно-перпенди­ку­лярных осей, проходящих через полюс, т. е.

Центробежным моментом инерции площади относительно координатных осей называется сумма произведений элементарных площадок dA на их расстояния до осей, взятая по всей площади:

.

Моменты инерции площади обычно измеряют в сантиметрах в 4-й степени (см⁴). Осевые и полярный моменты инерции площади всегда положительны, а центробежный момент инерции площади может быть любого знака или равняться нулю.

42.Деформация сдвига. Условия прочности при расчете на срез, на смятие, на разрыв.

Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис. 1).

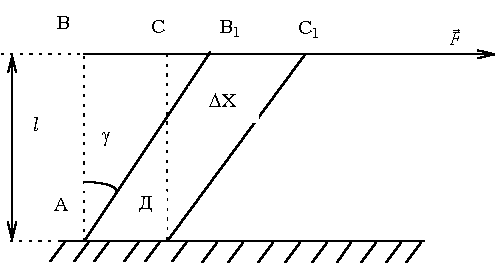
Рис.1

Сдвиг происходит под действием касательной силы F, приложенной к грани ВС, параллельной плоскости сдвига. Грань АД, параллельная ВС, закреплена неподвижно. Так как угол мал, формулу можно записать в виде:

(1)

где СС₁ =  X - абсолютный сдвиг,

  - угол сдвига, называемый также относительным сдвигом, выражается в радианах.

По закону Гука относительный сдвиг  пропорционален касательному напряжению F/S, где S - площадь поверхности грани ВС, т.е.

(2)

г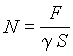 де N - модуль сдвига.

(3)

Модуль сдвига равен касательному напряжению, которое возникло бы в образце при относительном сдвиге, равном 1 (при условии, что закон Гука выполняется).

Условие прочности на сдвиг (срез) может быть записано в обычном виде:

.               

Условие прочности на смятие имеет вид: